Método de Euler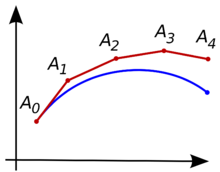

Ilustração do método de Euler. A curva desconhecida está em azul, e sua aproximação polinomial está em vermelho.[1]

Em matemática e ciência computacional, o método de Euler, cujo nome relaciona-se com Leonhard Euler, é um procedimento numérico de primeira ordem para solucionar equações diferenciais ordinárias com um valor inicial dado. É o tipo mais básico de método explícito para integração numérica para equações diferenciais ordinárias.

Formulação do Método de Euler

Suponha que queremos aproximar a solução de um problema de valor inicial:

${\displaystyle y'(t)=f(t,y(t)),\qquad \qquad y(t_{0})=y_{0}.}$

Escolhendo um valor para ${\displaystyle h}$ para o tamanho de cada passo e atribuindo a cada passo um ponto dentro do intervalo, temos que ${\displaystyle t_{n}=t_{0}+nh}$. Nisso, o próximo passo ${\displaystyle t_{n+1}}$ a partir do anterior ${\displaystyle t_{n}}$ fica definido como ${\displaystyle t_{n+1}=t_{n}+h}$, então: [2]

${\displaystyle y_{n+1}=y_{n}+hf(t_{n},y_{n}).}$ Com isso, para um valor menor de ${\displaystyle h}$ teremos mais passos dentro de um dado intervalo, mas que terá melhor aproximação com o valor analítico.

O valor de ${\displaystyle y_{n}}$ é uma aproximação da solução da EDO no ponto ${\displaystyle t_{n}}$: ${\displaystyle y_{n}\approx y(t_{n})}$. O Método de Euler é explícito, ou seja, a solução ${\displaystyle y_{n+1}}$ é uma função explícita de ${\displaystyle y_{i}}$ para ${\displaystyle i\leq n}$.

Enquanto o Método de Euler integra uma EDO de primeira ordem, qualquer EDO de ordem N pode ser representada como uma equação de primeira ordem: tendo a equação

${\displaystyle y^{(N)}(t)=f(t,y(t),y'(t),\ldots ,y^{(N-1)}(t))}$,

temos a introdução de variáveis auxiliares ${\displaystyle z_{1}(t)=y(t),z_{2}(t)=y'(t),\ldots ,z_{N}(t)=y^{(N-1)}(t)}$ obtendo a seguinte equação:

${\displaystyle \mathbf {z} '(t)={\begin{pmatrix}z_{1}'(t)\\\vdots \\z_{N-1}'(t)\\z_{N}'(t)\end{pmatrix}}={\begin{pmatrix}y'(t)\\\vdots \\y^{(N-1)}(t)\\y^{(N)}(t)\end{pmatrix}}={\begin{pmatrix}z_{2}(t)\\\vdots \\z_{N}(t)\\f(t,z_{1}(t),\ldots ,z_{N}(t))\end{pmatrix}}}$

Este é um sistema de primeira ordem na variável ${\displaystyle \mathbf {z} (t)}$ e pode ser usada através do Método de Euler ou qualquer outros métodos de resoluções de sistemas de primeira ordem.[3]

Exemplo

Dado o problema de valor inicial

${\displaystyle y'=y,\quad y(0)=1,}$

vamos usar o método de Euler para aproximar ${\displaystyle y(4)}$.[4]

Usando um passo igual a 1 (h = 1)

Ilustração da integração numérica para o exemplo ${\displaystyle y'=y,y(0)=1.}$[5] A curva em Azul é o método de Euler com h = 1.0.; em Verde, o ponto médio e em Vermelho, o valor exato da solução, ${\displaystyle y=e^{t}.}$

O método de Euler é

${\displaystyle y_{n+1}=y_{n}+hf(t_{n},y_{n}).\qquad \qquad }$

Primeiramente devemos aplicar o ponto ${\displaystyle f(t_{0},y_{0})}$. Nesse exemplo, a função ${\displaystyle f}$ é definida por ${\displaystyle f(t,y)=y}$. Nisso, temos que

${\displaystyle f(t_{0},y_{0})=f(0,1)=1.\qquad \qquad }$

Através do passo acima, vemos que a declividade da linha é tangente à solução da curva no ponto ${\displaystyle (0,1)}$. Lembre que a declividade é definida como a variação numérica de ${\displaystyle y}$ em relação a ${\displaystyle t}$, ou ${\displaystyle \Delta y/\Delta t}$.

O próximo passo é multiplicar o valor acima pelo tamanho do passo ${\displaystyle h}$, que nesse caso resultará em:

${\displaystyle h\cdot f(y_{0})=1\cdot 1=1.\qquad \qquad }$

Como o tamanho do passo é a variação em ${\displaystyle t}$, quando multiplicamos esse passo pela declividade da tangente, resultamos em um novo valor para ${\displaystyle y}$. Esse valor é então colocado ao valor de ${\displaystyle y}$ inicial, com o objetivo de obtermos o próximo valor para ser usado de modo recursivo.

${\displaystyle y_{0}+hf(y_{0})=y_{1}=1+1\cdot 1=2.\qquad \qquad }$

Os passos acima devem ser repetidos para assim encontrarmos ${\displaystyle y_{2}}$, ${\displaystyle y_{3}}$ e ${\displaystyle y_{4}}$.

${\displaystyle {\begin{aligned}y_{2}&=y_{1}+hf(y_{1})=2+1\cdot 2=4,\\y_{3}&=y_{2}+hf(y_{2})=4+1\cdot 4=8,\\y_{4}&=y_{3}+hf(y_{3})=8+1\cdot 8=16.\end{aligned}}}$

Como isso se torna um processo repetitivo, uma boa forma de organizar cada iteração em forma de tabela, evitando a possibilidade de erros.

${\displaystyle n}$	${\displaystyle y_{n}}$	${\displaystyle t_{n}}$	${\displaystyle f(t_{n},y_{n})}$	${\displaystyle h}$	${\displaystyle \Delta y}$	${\displaystyle y_{n+1}}$
0	1	0	1	1	1	2
1	2	1	2	1	2	4
2	4	2	4	1	4	8
3	8	3	8	1	8	16

A conclusão desse método é de que ${\displaystyle y_{4}=16}$, enquanto a solução exata da equação diferencial é ${\displaystyle y(t)=e^{t}}$, então ${\displaystyle y(4)=e^{4}\approx 54,598}$. Nesse caso, a aproximação por Método de Euler não é muito eficiente, porém podemos ver na imagem que o comportamento de ambas as curvas são semelhantes.

Usando outros tamanhos para h

A mesma ilustração para h = 0.25.

Como mostrado no início, o método possui sua aproximação aprimorada quando tomamos valores cada vez menores para ${\displaystyle h}$. A tabela abaixo mostra o resultado para diferentes tamanhos de ${\displaystyle h}$. A primeira linha são os valores para ${\displaystyle h=1}$, conforme descrito no tópico anterior. Já a segunda linha é para ${\displaystyle h=0,25}$, conforme ilustrado ao lado.

Tamanho de ${\displaystyle h}$	Resultado do Método de Euler	Erro Absoluto
1	16	38,598
0,25	35,53	19,07
0,1	45,26	9,34
0,05	49,56	5,04
0,025	51,98	2,62
0,0125	53,26	1,34

O erro absoluto é a diferença entre o valor obtido por Euler e o valor exato da solução para ${\displaystyle t=4}$. Podemos ver que, ao ponto que o valor de ${\displaystyle h}$ vai caindo pela metade a cada linha, o erro aproximadamente possui o mesmo comportamento. Isso sugere que o erro absoluto é relativamente proporcional ao tamanho do passo de cada iteração adotado. Essa notação perde a validade para passos muito pequenos, mas geralmente é válida em demais equações; consulte Erro de truncamento para mais detalhes.

Em outros métodos ilustrados, como o Método dos Pontos Médios neste caso mostraram-se mais razoáveis, pois este possui uma precisão proporcional quadrática do tamanho do passo. Por essa razão, tem-se o Método de Euler como um método de primeira ordem, enquanto o Método dos Pontos Médios é dito como de segunda ordem.

Podemos extrapolar a tabela acima se precisamos de uma melhor precisão através da escolha de valores como ${\displaystyle h=0,00001}$ que, para chegar em ${\displaystyle t=4}$, necessitamos de 400.000 passos. Esse método demanda, portanto, um grande custo computacional; com isso, usam-se métodos com maior ordem de precisão, como o Método de Runge-Kutta, quando uma grande aproximação é necessária.[6]

Método de Euler contra métodos de ordem maior

A ordem de um método mede o quão rapidamente este converge para a solução analítica quando se diminui os passos na integração numérica [7]. Infelizmente devido a limitações computacionais, erros de arredondamento crescem quando se diminui o tamanho dos passos, ocorrendo até mesmo divergência ou mesmo valores errados. Uma forma de resolver este problema é aumentar a ordem do método numérico. Por exemplo, métodos de ordem maiores incluem método de Runge-Kutta e o método de Euler melhorado.

Notas

1. «Faça exemplos com O Monitor». omonitor.io. Consultado em 23 de março de 2016 
2. Butcher 2003, p. 45; Hairer, Nørsett & Wanner 1993, p. 36
3. Butcher 2003, p. 3; Hairer, Nørsett & Wanner 1993, p. 2
4. Veja Também Atkinson 1989, p. 344
5. «Confira este exemplo e faça outros com O Monitor». omonitor.io. Consultado em 23 de março de 2016 
6. Hairer, Nørsett & Wanner 1993, p. 40
7. Devries, Paul L. ; Hasbun, Javier E. A first course in computational physics. Second edition. Jones and Bartlett Publishers: 2011.

Ver também

• Para métodos numéricos para cálculo de integrais definidas, veja integração numérica.