|
Exemplos de Máquinas de TuringOs exemplos a seguir são para complementar o artigo Máquina de Turing. Primeiro exemplo de Máquina de TuringA tabela a seguir é o primeiro exemplo (Alan Turing 1937):
Com relação às ações que a máquina realmente executa, Turing (1936) (Indecidível p. 121) afirma o seguinte:
Ele deixa isso muito claro quando ele reduz a tabela acima para uma única instrução chamado de "b" (Indecidível p. 120), mas sua instrução consiste em 3 linhas. Instrução "b" tem três possibilidades diferentes de símbolos {Nenhum, 0, 1}. Cada possibilidade é seguido por uma seqüência de ações até que cheguemos a coluna mais à direita, onde o m-configuração final é "b":
Como observado por um número de influenciadores, incluindo o próprio Turing (1937), (por exemplo, Post (1936), Post (1947), Kleene (1952), Wang (1954)) as instruções de Turing não são atômicas — outras medidas de simplificação do modelo podem ser feitas sem reduzir o seu poder computacional; veja mais em Máquina de Post-Turing. Como se afirma no artigo Máquina de Turing, Turing propôs que a tabela ainda ser atomizada, permitindo que apenas uma única imprimir/apagar seguido por uma fita simples movimento E/R/D. Ele nos dá este pequeno exemplo da primeira tabela convertida (Indecidível, p 127.):
A declaração de Turing ainda implica cinco operações atômicas. A uma dada instrução (m-configuração) da máquina:
Como as ações de uma máquina de Turing não são atômicas, uma simulação da máquina deve atomizar cada 5-tupla em uma seqüência de ações mais simples. Uma possibilidade — utilizado nos seguintes exemplos de "comportamentos" de sua máquina — é como se segue:
O chamado "canonical" Máquina de estados finitos faz os testes de símbolos "em paralelo"; veja mais em Microcode. No exemplo a seguir do que a máquina faz, observamos algumas peculiaridades dos modelos de Turing:
Assim, quando a impressão que ele ignora todos os outros quadrados. Os quadrados impressos são chamados F-quadrados; os quadrados em branco no meio podem ser utilizados para "marcadores" e são chamados de "E-quadrados" como em "susceptível de apagamento." Os F-quadrados, por sua vez são os seus "Figuras quadrados" e só vai arcar com os símbolos 1 ou 0 — símbolos que ele chamou de "figuras" (como em "números binários"). Neste exemplo, a fita começa "em branco", e os "dados" são então impressas sobre ele. Para abreviar apenas a tabela-estados são mostrados aqui:
A mesmo "execução" com toda a fita-impressão intermediária e os movimentos são mostrado aqui: Um olhar mais atento sobre a tabela revela certos problemas com o próprio exemplo &mdash de Turing, nem todos os símbolos são contabilizados. Por exemplo, suponha que sua fita não foi inicializada em branco. O que aconteceria? A máquina de Turing iria ler valores diferentes do que os valores pretendidos. Uma cópia da sub-rotinaEste é um importante sub-rotina muito utilizado na rotina "multiplicar". A máquina de Turing exemplo lida com uma série de 0s e 1s, com 0 representado pelo símbolo em branco. Sua tarefa é dobrar qualquer série de 1s encontradas na fita escrevendo um 0 entre eles. Por exemplo, quando a cabeça lê "111", vai escrever um 0, em seguida, "111". A saída será "1110111". A fim de cumprir a sua missão, esta máquina de Turing vai precisar apenas 5 estados de operação, que são chamados {s1, s2, s3, s4, s5}.Cada estado faz 4 ações:
Uma "execução" das sequências da máquina através de 16 máquinas-configurações (também conhecido como "estados de Turing"):
O comportamento da máquina pode ser descrito como um circuito: ele começa em s1, substitui o primeiro 1 com um 0, em seguida, usa s2 para mover para a direita, pulando 1s e o primeiro 0 encontrado. s3, em seguida, salta a próxima seqüência de 1s (inicialmente não há nenhuma) e substitui o primeiro 0 que encontra com um 1. s4 move para a esquerda, pulando 1s até encontrar um 0 e muda para s5. s5 então se move para a esquerda, pulando 1s até encontrar o 0 que foi originalmente escrito por s1. Ele substitui aquele 0 por um 1, move uma posição para a direita e digita s1 novamente para mais uma rodada do loop. Isso continua até que s1 encontra um 0 (esta é a 0 no meio das duas seqüências de 1s), momento em que pára a máquina. Descrição alternativaOutra descrição vê o problema como a forma de manter o controle de quantos "1"s existem. Nós não podemos usar um estado para cada número possível (um para cada estado de 0,1,2,3,4,5,6 etc), porque então precisaríamos de estados infinitos para representar todos os números naturais, e a máquina de estado é finita - nós vamos ter que controlar isso usando a fita de alguma forma. A forma básica é que funciona, copiando cada "1" para o outro lado, movendo-se para trás e para frente - é inteligente o suficiente para lembrar que parte da viagem está conectado. Em mais detalhe, ele carrega cada "1" para o outro lado, através do reconhecimento da separação "0" no meio, e reconhecendo a "0", por outro lado para saber que é atingido o fim. Ele volta usando o mesmo método, o meio de detecção "0", e, em seguida, a "0" no lado original. Este "0" no lado original é a chave para o enigma de como ele mantém o controle do número de 1s. O truque é que antes de colocar o "1", marca que dígito como "feito", substituindo-o com um "0". Quando ele retorna, ele preenche de que "0" para trás com um "1", passa então para o próximo, marcando-o com um "0" e repetindo o ciclo, levando que "1" de diâmetro e de forma ligar. Com cada viagem em frente e para trás, o marcador de "0" se move um passo mais perto do centro. É assim que mantém o controle de quantos "1" 's que os tomou durante. Curiosamente, quando ele retorna, o marcador "0" parece ser o fim da recolha de "1" s para isso - qualquer "1" s que já foram tomadas através são invisíveis a ele (do outro lado do marcador "0 ") e por isso, é como se está a trabalhar sobre um número (N-1) de" 1 "s - semelhante a uma prova por Indução matemática. Uma completa "execução" mostra os resultados de "movimentos" intermediários. Para vê-lo melhor, clique na imagem, em seguida, clique na maior resolução de download: Algoritmo do castor de 3 estadosA seguinte tabela Turing de instruções foi derivado de Peterson (1988) página 198, Figura 7.15. Peterson move a cabeça; no seguinte modelo a fita se move.
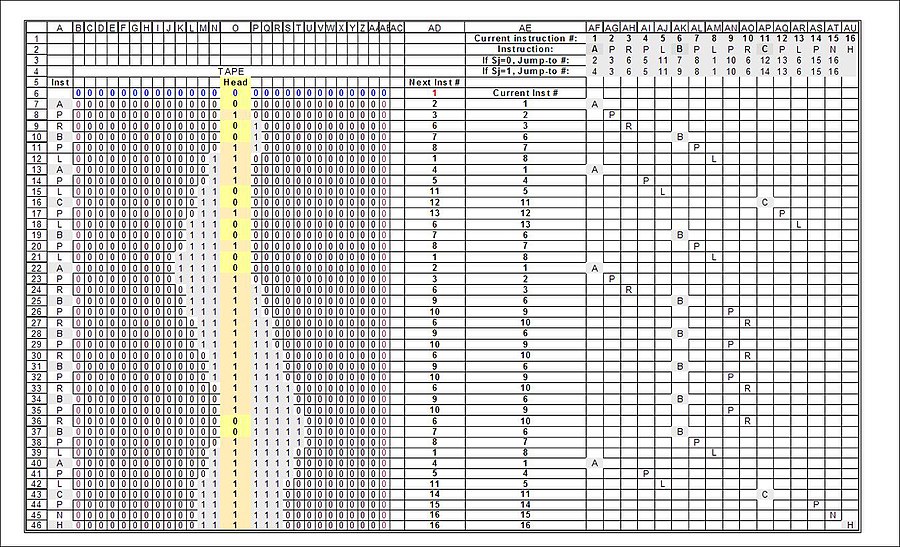
O desenho "estado" do castor ocupado 3-estados mostra as sequências internas de eventos necessários para realmente executar "o estado". Como observado acima, Turing (1937) deixa perfeitamente claro que esta é a interpretação adequada dos 5-tuplas que descrevem a instrução (Indecidíveis, p. 119). Para saber mais sobre a atomização de Turing 5-tuplas ver Máquina de Post-Turing: A tabela a seguir mostra o "comprimido" da execução e & mdash; apenas o Turing afirma:
A "execução" completa do castor ocupado 3-estados. Os resultantes do estados de Turing (o que Turing denominados "configurações-m" & mdash; "máquinas-configurações") são mostrados em destaque em cinza na coluna A, e também sob instruções da máquina (colunas AF-AU)) BibliografiaPara ver referências completas Máquina de Turing.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||