|
Controlador proporcional integral derivativoControlador proporcional integral derivativo, controlador PID ou simplesmente PID, é uma técnica de controle de processos que une as ações derivativa, integral e proporcional, fazendo assim com que o sinal de erro seja minimizado pela ação proporcional, zerado pela ação integral e obtido com uma velocidade antecipativa pela ação derivativa. É baseado na resposta de uma malha de processo industrial a ser controlada. Na prática os PID são encontrados no interior de controladores eletrônicos chamados "single-loop", muitas vezes com microprocessadores, e também através de Controladores programáveis e outros equipamentos de controle.[1] Os controladores contínuos podem controlar os processos de três formas distintas: • Controle Proporcional (P); • Controle Integral (PI); • Controle Derivativo (PD); Estes três modos de controle são também designados de ações de controle, cada uma delas reagindo de forma distinta ao erro presente nos sistemas e consequentemente minimizando a variação de erro. O controle proporcional ajusta a variável de controle de forma proporcional ao erro. O controle integral ajusta a variável de controle baseando-se no tempo em que o erro acontece. O controle derivativo ajusta a variável de controle tendo como base a taxa de variação do erro. A combinação destes tipos de controle forma o controlador conhecido na indústria como PID. Algoritmo PIDDefinindo como o sinal de saída, o algoritmo PID pode ser definido por: onde
Aplicando a transformada de Laplace, obtemos: onde
A Ação proporcional A ação proporcional produz um sinal de saída que é proporcional à amplitude do erro e(t), sendo a constante de proporcionalidade:
Comparado com a ação liga-desliga, esse método possui a vantagem de eliminar as oscilações do sinal de saída. Para tal, o sistema permanece sempre ligado e o sinal de saída é diferente de zero. Tendo em vista que o sinal de saída é proporcional ao erro, um erro não-nulo (conhecido por erro de off-set) é gerado. O valor do erro off-set é inversamente proporcional ao ganho e pode ser compensado adicionando-se um termo ao valor de referência ou pelo controle integral. Um ganho proporcional muito alto gera um alto sinal de saída, o que pode desestabilizar o sistema. Porém, se o ganho proporcional é muito baixo, o sistema falha em aplicar a ação necessária para corrigir os distúrbios. Ação Integral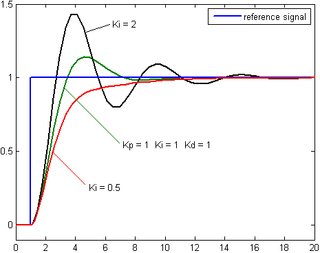 A ação integral produz um sinal de saída que é proporcional à magnitude e à duração do erro, ou seja, ao erro acumulado. Isso fornece uma alternativa para corrigir o erro de off-set gerado pela ação proporcional e acelera a resposta do sistema, permitindo-o chegar ao valor de referência mais rapidamente. O sinal de saída do controlador PI pode ser descrito por :
onde é o ganho integral. A ação integral corrige o valor da variável manipulada em intervalos regulares, chamado tempo integral. Esse tempo integral é definido como o inverso do ganho integral. Se o ganho integral é baixo, o sistema pode levar muito tempo para atingir o valor de referência. No entanto, se o ganho integral for muito alto, o sistema pode tornar-se instável. Ação Derivativa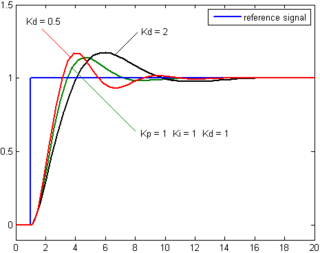 A ação derivativa produz um sinal de saída que é proporcional à velocidade de variação do erro:
onde Kd é o ganho derivativo. A ação derivativa fornece uma correção antecipada do erro, diminuindo o tempo de resposta e melhorando a estabilidade do sistema.[2][3] A ação derivativa atua em intervalos regulares, chamado tempo derivativo. Esse parâmetro é inversamente proporcional à velocidade de variação da variável controlada. Isso indica que a ação derivativa não deve ser utilizada em processos nos quais o sistema deve responder rapidamente a uma perturbação, nem em processos que apresentem muito ruído no sinal de medido, pois levaria o processo à instabilidade. Ajuste de ParâmetrosO ajuste de parâmetros do controlador PID pode ser feito manualmente ou através de métodos de optimização como o método de Ziegler-Nichols. Nesse método, os ganhos e são primeiramente ajustados para zero. Em seguida, aumentamos o ganho proporcional até que o sinal de saída começa a oscilar. Isso define um ganho crítico, , e um período crítico, . Os ganhos dos controladores P, PI, PID são então ajustados conforme a tabela abaixo:
Tendo em vista que o ganho proporcional do controlador P é apenas a metade do ganho crítico, esse sistema possui uma boa margem de ajuste.[4] Devido ao efeito desestabilizante da ação integral, o ganho proporcional reduz para 0.45 do ganho crítico. Contudo, o efeito estabilizante da ação derivativa permite aumentar o ganho proporcional para 0.6 do ganho crítico no controlador PID. História do controlador PIDEm seu TCC, Felipe Fernandes França conta que desde o início da Revolução Industrial, surgiu a necessidade de controlar sistemas e processos industriais. Inicialmente, o controle manual era predominante, onde operadores habilidosos ajustavam o processo manualmente. No entanto, com a crescente automação, essa abordagem tornou-se cada vez mais desafiadora devido à complexidade dos sistemas. Isso impulsionou a busca por soluções, atraindo a atenção de acadêmicos e inventores. Em 1788, James Watt desenvolveu o "governador centrífugo" (flyball governor), um dispositivo mecânico que regulava a velocidade de motores a vapor controlando o vapor admitido. Esse sistema pioneiro operava com um controle proporcional (P), ajustando a quantidade de vapor com base na velocidade do motor, mantendo-a constante para diferentes cargas. No entanto, o controle proporcional sozinho não conseguia eliminar o erro em regime permanente. Em torno dos anos 1930, surgiu a ideia de adicionar uma componente integral (I) para zerar esse erro. O controlador resultante, conhecido como Proporcional-Integral (PI), resolveu parte do problema, mas também introduziu novas questões, como sobressinal máximo e oscilações excessivas. A evolução continuou, e em 1940, a Taylor Instrument Companies lançou o primeiro controlador Proporcional-Integral-Derivativo (PID) pneumático. A ação derivativa (D) foi introduzida para mitigar problemas do controlador PI, reduzindo o sobressinal e as oscilações. No entanto, a adoção dos controladores PID era limitada devido às dificuldades de ajuste e à tecnologia pneumática da época. O cenário mudou em 1942 com o artigo "Optimum settings for automatic controllers" de Ziegler e Nichols. Eles apresentaram um método simplificado de sintonia, impulsionando a popularidade dos controladores PID. A ascensão dos transistores e o método de sintonia de Ziegler e Nichols marcaram o fim dos controladores pneumáticos, permitindo a criação de controladores PID eletrônicos com alta capacidade de processamento. Hoje, uma variedade de métodos de sintonia e tecnologias de implementação de controladores PID está disponível. Muitos estão integrados a controladores lógicos programáveis, oferecendo sintonia automática e segura, como o método do relé. Esses avanços transformaram os controladores PID em uma ferramenta indispensável para controlar sistemas e processos complexos em várias indústrias.[5](FELIPE FERNANDES FRANÇA, 2018).
Referências
|




















