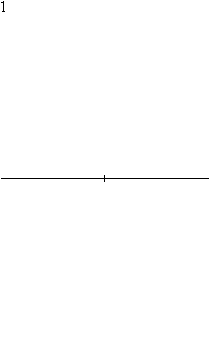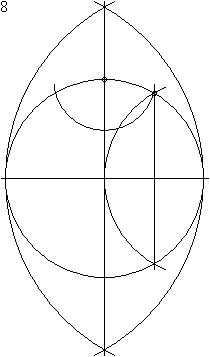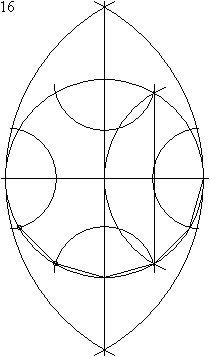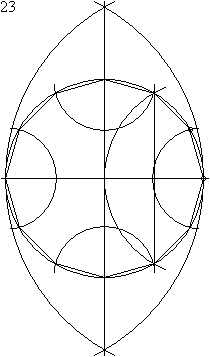Regelmatige twaalfhoek Een twaalfhoek of dodecagoon is een veelhoek met twaalf hoeken en twaalf zijden . Een regelmatige twaalfhoek is een regelmatige veelhoek met twaalf gelijke hoeken en twaalf gelijke zijden. De hoeken van een regelmatige twaalfhoek zijn met
n
=
12
{\displaystyle n=12}
α
=
(
n
−
2
)
n
⋅
180
∘
=
10
12
⋅
180
∘
=
150
∘
{\displaystyle \alpha ={\frac {(n-2)}{n}}\cdot 180^{\circ }={\frac {10}{12}}\cdot 180^{\circ }=150^{\circ }}
Oppervlakte
De oppervlakte
A
{\displaystyle A}
a
{\displaystyle a}
A
=
3
cot
(
π
12
)
a
2
=
3
(
2
+
3
)
a
2
≈
11,196
15242
a
2
{\displaystyle {\begin{aligned}A&=3\cot \left({\frac {\pi }{12}}\right)a^{2}=3\left(2+{\sqrt {3}}\right)a^{2}\\&\approx 11{,}19615242\,a^{2}\end{aligned}}}
Als
R
{\displaystyle R}
straal van de omgeschreven cirkel is, geldt:
A
=
6
sin
(
π
6
)
R
2
=
3
R
2
{\displaystyle A=6\sin \left({\frac {\pi }{6}}\right)R^{2}=3R^{2}}
Als
r
{\displaystyle r}
straal van de ingeschreven cirkel is, geldt:
A
=
12
tan
(
π
12
)
r
2
=
12
(
2
−
3
)
r
2
≈
3,215
3903
r
2
{\displaystyle {\begin{aligned}A&=12\tan \left({\frac {\pi }{12}}\right)r^{2}=12\left(2-{\sqrt {3}}\right)r^{2}\\&\approx 3{,}2153903\,r^{2}\end{aligned}}}
Constructie van een regelmatige twaalfhoek
Het construeren met passer en liniaal van een regelmatige twaalfhoek geschiedt in 23 stappen: