|
Sprouts Sprouts is een wiskundig spel dat gespeeld wordt door twee spelers met pen en papier. Het werd bedacht door John Conway en Michael S. Patterson aan de universiteit van Cambridge begin jaren 60 van de twintigste eeuw. Conway en anderen hebben dit spel grondig geanalyseerd. RegelsHet spel begint met een aantal punten op een vel papier. De spelers spelen om beurt. In elke beurt trekt de speler een lijn tussen twee punten of een lus van een punt naar hetzelfde punt, en tekent een nieuw punt op die lijn. Daarbij moet de speler de volgende regels respecteren:
Gebogen lijnen zijn toegestaan. De speler die geen geldige lijn meer kan trekken, verliest; dit is de "normale" versie van Sprouts. Een gelijkspel is onmogelijk. Aantal zetten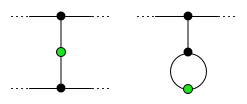 Hoewel er in elke zet een punt bij komt, is het aantal zetten in een spel Sprouts beperkt. Als er n punten zijn bij het begin, is het aantal zetten minimaal 2n en maximaal 3n-1. Men kan dit inzien door het aantal "levens" of vrijheidsgraden van een punt te beschouwen; dit is het aantal lijnen dat er nog aan kan worden toegevoegd. Een punt waar drie lijnen samenkomen heeft nul levens; het is een dood punt. Bij het begin van een spel met n punten zijn er 3n levens. In elke beurt gaan twee levens verloren, terwijl er een punt bij komt met slechts 1 leven. Het totaal aantal levens vermindert dus in elke beurt met 1. aantal beurten heeft en geen gelijkspel, bestaat er een winnende strategie voor de eerste of de tweede speler, naargelang het aantal punten bij het begin. Voor een klein aantal beginpunten kan men die met de hand bepalen maar deze analyse wordt al snel ingewikkeld. David Applegate, Guy Jacobson en Daniel Sleator berekenden in 1990 met een computer de uitkomst voor Sprouts tot elf punten.[1] In 2011 bedachten Julien Lemoine en Simon Viennot een efficiënt algoritme en bepaalden wie de winnaar van normale Sprouts is voor spellen tot 44 beginpunten.[2] De uitkomsten voor de eerste speler zijn:
Applegate, Jacobson en Sleator observeerden dat de eerste speler wint wanneer het aantal beginpunten n modulo zes gelijk is aan drie, vier of vijf. De eerste speler verliest wanneer n modulo 6 gelijk is aan 0, 1 of 2. De resultaten van Lemoine en Simon bevestigden dit vermoeden. Bronnen, noten en/of referenties
|