Polyconische projectie

Polyconische projectie
Gunstige eigenschap	afstandsgetrouw langs parallellen
Geometrische constructie
Vorm van het projectievlak	kegel (variabel)
Positie van het projectievlak	normaal
Rakend/snijdend	rakend
Portaal    Geografie

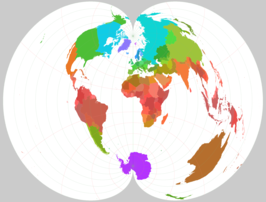
De polyconische projectie is een variant op de kegelprojectie waarbij de tophoek van de kegel varieert met het af te beelden punt. Het resultaat is een kaart met constante schaal in de richting van de parallellen, die de vorm hebben van een deel van een cirkel.

De projectie wordt gegeven door:

${\displaystyle x\,=\cot \beta \sin(\lambda \sin \beta )}$

${\displaystyle y\,=\beta +\cot \beta [1-\cos(\lambda \sin \beta )]}$

Ferdinand Rudolph Hassler stelde deze projectie voor in 1825. Na 1879 werd de polyconische projectie al gauw favoriet bij Amerikaanse overheidsinstanties, waardoor er op den duur ook kaarten op basis van deze projectie in commerciële atlassen verschenen. Sinds het midden van de 20e eeuw wordt de polyconische projectie echter niet veel meer gebruikt.

Zie ook

Strikte kegelprojecties:

• Hoekgetrouwe kegelprojectie
• Oppervlaktegetrouwe kegelprojectie

Andere afstandsware projecties:

• Tweepunts-equidistante projectie