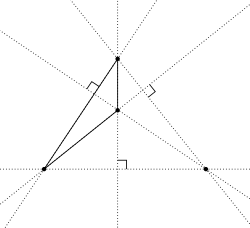
Hoogtepuntsysteem Een hoogtepuntssysteem is een viertal punten dat bestaat uit de hoekpunten van een driehoek samen met het hoogtepunt van die driehoek. De naam vindt zijn oorsprong in het feit dat ieder punt het hoogtepunt is van de driehoek gevormd door de andere drie punten.
De middelpunten van de ingeschreven cirkel en de drie aangeschreven cirkels van een driehoek ABC vormen een hoogtepuntssysteem, hun gezamenlijke negenpuntscirkel is de omgeschreven cirkel van driehoek ABC.
Eigenschappen
De vier mogelijke driehoeken die met de punten van een hoogtepuntssysteem gevormd kunnen worden, hebben alle dezelfde negenpuntscirkel.
De vier driehoeken ABC, ABD, ACD en BCD van het hoogtepuntssysteem ABCD hebben alle dezelfde straal van hun omgeschreven cirkels .
Is ABCD een hoogtepuntssysteem, dan geldt:
A
B
2
+
C
D
2
=
A
C
2
+
B
D
2
=
A
D
2
+
B
C
2
=
4
R
2
{\displaystyle AB^{2}+CD^{2}=AC^{2}+BD^{2}=AD^{2}+BC^{2}=4R^{2}}
waarin R de gemeenschappelijke straal is van de omgeschreven cirkels van de driehoeken met punten uit ABCD.
Zie ook