|
Z階数曲線 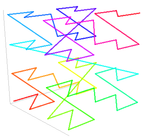  解析学、計算機科学、数学的な関数など分野ごとに、 Z階数、 ルベーグ曲線、 モートン階数 あるいは モートン符号 などと呼ばれ、多次元のデータをその局所部位の部分データを保持したまま1次元に写像する手法である。本手法は 1966 年に ガイ・マクドナルド・モートン により発表された。[1]この手法では多次元のデータに含まれるある点の部分データを、その点の座標値の2進符号化に現れる交互配置性を基に単純な計算による z値 として表す。一度、この階数によりデータを再配置すれば、2分木、B木、スキップリスト、ハッシュテーブルなどのあらゆる1次元のデータを扱う構造が適用可能となる。これは 4分木 の深度優先探索とも等価である。 データ構造と座標値群の取り扱い下図に 2次元における z値 について整数の座標群 0 ≤ x ≤ 7, 0 ≤ y ≤ 7 (10進数と2進数で表示)の範囲で図示する。2進数の相互配置的な並びに着目すると、2進数で表した座標値(=インデックス値)には2進数の z値 が含まれる。 z値 を数値的に昇順に繋げるとZ字型の曲線が生成される。2次元におけるZ値群は quadkey (意訳; 四つ子の鍵)とも呼ばれる。  座標のx値はZ値にモーサー-ドブリュン数列(英語: Moser–de Bruijn sequence)による2進数値群として0ビット目、2ビット目、4ビット目のように偶数ビット群に現れる: x[] = {0b000000, 0b000001, 0b000100, 0b000101, 0b010000, 0b010001, 0b010100, 0b010101}
2つのx値の和と差はビット単位演算により計算できる: x[i+j] = ((x[i] | 0b10101010) + x[j]) & 0b01010101 x[i-j] = ((x[i] & 0b01010101) - x[j]) & 0b01010101 但し i >= j の場合 この性質から、現在の z値 の座標を右(x値を増加)、左(x値を減少)、下(y値を増加)、上(y値を減少)へオフセットした他の座標の z値を計算できる: 上 = ((z & 0b10101010) - 1 & 0b10101010) | (z & 0b01010101) 下 = ((z | 0b01010101) + 1 & 0b10101010) | (z & 0b01010101) 左 = ((z & 0b01010101) - 1 & 0b01010101) | (z & 0b10101010) 右 = ((z | 0b10101010) + 1 & 0b01010101) | (z & 0b10101010) 2つの2次元のZ値群に一般化すると: 和 = ((z | 0b10101010) + (w & 0b01010101) & 0b01010101) | ((z | 0b01010101) + (w & 0b10101010) & 0b10101010) 4分木の効率的な構築への応用Z階数曲線の応用により4分木を効率的に構築できる。[2]基本戦略としてz値に基いた並べ替えを施す。一度この並べ替えを済ませれば、格納されたデータに対し直接的に2分木探索を行える線形4分木構造となる。[3] 通常、入力点群は次元ごとに正の整数へ正規化し機械語が対応するサイズとするが、範囲 [ 0, 1 ] の固定小数点表現とする事もある。何れにせよ最上位の非零のビットは定数時間で探索可能となる。4分木の内包する4つの正方形は辺の長さが2の冪乗で、角の座標は辺の長さの倍数となる。このうちの2点を決定すれば、その両方の点に囲まれた derived square ( 子要素の正方形 )も決まる。なお、この手法では x 要素と y 要素のビット群の相互配置性は shuffle ( 混ぜ合わせ )と呼ぶ。これらの特徴はより高次元に対しても拡張できる。[2] 点群は実際にビットの相互配置をせずとも shuffle からソート可能である。先ず次元ごとに、2点の最上位ビットの排他的論理和を評価し、次に最上位ビットが最大の次元で shuffle の順位を決める。 排他的論理和は2点の座標が同一の場合最上位ビットをマスクする。shuffle は上位から下位へとビットを相互配置するので、最大の最上位ビットを持つ座標を識別でき、異なる shuffle 順位の最初のビットも識別でき、よって2点の座標を比較できる。[4] 以下に Python のソースコードを示す: def cmp_zorder(a, b):
j = 0
k = 0
x = 0
for k in range(dim):
y = a[k] ^ b[k]
if less_msb(x, y):
j = k
x = y
return a[j] - b[j]
各点で底2の対数の床値を比較していることが最も重要である。これは以下と等価であり、排他的論理和しか使用しない:[4] def less_msb(x, y):
return x < y and x < (x ^ y)
浮動小数点数についても同様に比較可能である。その場合、 less_msb 関数は最初に指数部を比較するよう変更する。そして指数部が等しい場合にのみ元の less_msb 関数を適用する。[5] 一度、点群が順位により並べ替えられたなら、次の2つの特性により4分木を容易に構築可能となる: 第1に、4分木の正方形に含まれる点群はz値による並べ替えにより隣接した相互配置を構築できる特性。第2に、ある正方形に2つ以上の点が含まれているならば、それは derived square (子要素の正方形)となっている特性。 derived square の隣接する点の対ごとの正方形の辺の長さは元となる最初の大きな正方形から計算できる。[2] derived square の相互配置ごとに4分木の正方形に相当する圧縮された4分木が得られ、ノード群には入力点または2つ以上の子要素が保存される。必要に応じて非圧縮の4分木も復元できる。 こうして、ポインターに基づいた4分木ではなく2分木のようなデータ構造で点群を維持できる。これにより、点の追加と削除は O(log n) 時間で可能となる。また、2つの4分木の結合も2つの並べ替え済みとした点群から行え、重複も削除できる。点の位置の前後の走査も容易にできる。[6] 1次元データ構造の範囲検索への適用局所性を良好に保ちながら効率的な範囲検索を行いたいようなアルゴリズムでは、データ構造内で遭遇した点から、次の多次元の探索範囲にあるZ値への計算が必要である:  この例では、照会したい範囲( x = 2,...,3, y = 2,...,6 )を点で囲まれる矩形で表した。このうちで最大のz値は MAX は 45 である。この例においては、照会対象をz値に基いて探索するうちに F = 19 に遭遇するため、 F と MAX の間のz値の範囲(斜線の領域)について探索が必要となる。探索を高速化として、照会したい範囲の未照会の範囲で最小のz値 BIGMIN (この例では 36 )を計算し、 BIGMIN と MAX の間の区間(太字の範囲)のみを探索する事で、斜線領域の多くを飛ばせる。もし、逆向きに探索する場合は BIGMIN と同様に、照会範囲内で F よりも小さな最大の Z値 LITMAX を計算する。この BIGMIN 問題は Tropf と Herzog に提起され解決されている。[7] この手法は UB木 の "GetNextZ-address" でも用いられる。この手法は元の1次元のデータ構造に依存せずデータを容易かつ自由に構造化可能なため、B木のような既知の手法を用いて動的データへ対応できる。(これはR木が特別な配慮を要する事と対照的である。) (元のデータ構造に従って)階層的にこの手法を適用すれば、増加方向、減少方向の何れであれ、非常に効率的な多次元の範囲検索を適用でき、最近傍探索の基礎として商用あるいは技術的にも重要である。Z階数を応用した多次元の商用データベースシステムがいくつか製品化されている(オラクルデータベース 1995,[8] en:Transbase 2000 [9])。 今は昔となる 1966 に、G.M.Morton が地理学的データベースの静的な2次元のファイル群についてZ階数を提案した。面のデータ単位には1つまたは幾つかの二次的な、Z値に基づいた枠を含んでいた。高確率で隣接フレーム間の参照を僅かな走査ステップで可能であった。 関連する構造代わりにヒルベルト曲線を用いれば、より優れた順序保存性を持つと提案されているが、計算が複雑となるためプロセッサーのオーバーヘッドが大きくなってしまう。Z曲線とヒルベルト曲線の両方についてBIGMINのソースコードが H. Tropf によるアメリカ合衆国の特許に記載されている。[10] 多次元のデータ処理、最近傍探索などについては ハナン・サメット(英語: Hanan Samet) の教科書が参考となる。[11] 応用群線形代数学行列の乗算に用いられるシュトラッセンのアルゴリズムでは行列を4つのブロックに分割し、ブロックが単一の要素となるまで各ブロックを再帰的に分割する手法に基づく(応用における実用上は適用したいアルゴリズムが十分に高速化できる程度まで分割する)。分割された2つのブロックを乗算するサブルーチンについては行列全体の大きさによらず、ブロックの大きさとメモリー配置(行優先、列優先)についてのみ扱えば良い。 ヴァルサラーム( Valsalam )とシェンヌム( Skjellum )による2002年の論文でZ階数のシュトラッセンの乗算への応用効果が実証されている。[12] Buluç らにより疎行列のデータ構造のの非零の要素における行列とベクターの乗算に対する並列アルゴリズムの有効化にも応用される。[13] テクスチャーマッピングいくつかのGPUではテクスチャーマップをZ階数により格納し、ラスタライズにおける空間の参照の局所性を向上している。これにより線形のキャッシュメモリー上へ正方形型のタイルを表現可能となり、二次元的な近傍の情報がキャッシュ内に収まっている確率が高まる。3Dレンダリングでは任意的な変形(アニメーションした表面の歪み、遠近法、拡縮、回転など)が必要とされるため重要な要素技術となっており、そのようなテクスチャー方式は スウィズルテクスチャー あるいは ツィードテクスチャー と呼ばれる。他のタイル化された形式についてもこの手法は同様に適用できる。 脚注
関連項目
外部リンク
|