PAD (ソフトウェア設計)

PAD（パド[1]、Problem Analysis Diagram）は、問題解析図とも呼ばれ、プログラムの制御構造を木構造的に表す図である。日立製作所の二村良彦、川合敏雄らによって開発された[2]。JIS X 0128 に「プログラム構成要素及びその表記法」としてフローチャートとともに規定されている[3]。

概要

プログラムの作成にあたっては、制御構造を表すフローチャートを作り、示された手順に基づいてコーディングしていくことが行われてきた。フローチャートは個々の処理記号（処理、判断、ループ、など）は決められているが、処理記号や接続する線の位置や方向が定められていないため、同じ手順が異なるチャートになったり、制御構造が判然としなくなるという欠点があった[1]。

さらに、構造化プログラミング技法が浸透することによってフローチャートの欠点は顕著になった。

PADはこの欠点を解消するために開発された2次元木構造図であり、ワーニエ図（英語版）を改良したものである[4][5]。

具体的には、プログラムの構造を、

  • 連接:単純な処理の連続
  • 選択:条件による処理の選択（分岐）
  • 反復:条件による処理の繰り返し

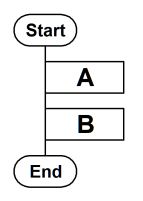
という内容に細分化していき、明確化していくことを目的としている。

そのため、PADでは各処理の記号と記号の接続方法を規定しておくことで、多くの場合、プログラム構造を表すPADはフローチャートに比べて作成者によるバラツキが少なくなる[6]。また、プログラムのソースとPADが対応しているのでコーディングを機械的に行うことが出来る[7]。

記述法

PADにおける各制御構造と対応するフローチャート、および、サンプル擬似コードを示す。なお、A、B…は処理（サンプルコードにおいては関数）、Q、R、C1〜Cx は選択や反復の条件など、選択におけるTはTrue、FはFalseを表すものとする。また、PADでは「Start」「End」の記号は必須ではないが、フローチャートとの比較用に用いている。

連接

処理「A」に続いて処理「B」を実行する例。

PAD フローチャート サンプルコード
連接処理のPAD例 連接処理のフローチャート例 
int sample(void)
{
    A();
    B();
}

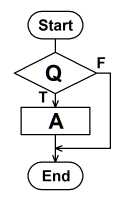
選択

条件「Q」の真偽によって処理を実行するか否かを選択する例。

if then型

条件「Q」が真の場合に処理「A」を実行する例。「if文(if...then)」に相当する。

PAD フローチャート サンプルコード
if then型選択処理のPAD例 if then型選択処理のフローチャート例 
int sample(void)
{
    if (Q)
        A();
}

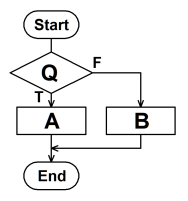
if then else型

各条件「Q」が真の場合に処理「A」を実行し、偽の場合に処理「B」を実行する例。「if文(if...then...else)」に相当する。。

PAD フローチャート サンプルコード
if then else型選択処理ののPAD例 if then else型選択処理ののフローチャート例 
int sample(void)
{
    if (Q)
        A();
    else
        B();
}

多分岐(switch case)型

「Q」に対しそれぞれの条件「Cn」が成立した場合に各処理を実行する例。「switch文」に相当する。

PAD フローチャート サンプルコード
case（多分岐）型選択のPAD例 case（多分岐）型選択のフローチャート例 
int sample(void)
{
    switch(Q){
        case C1:
            A();
            break;
        case C1:
            B();
            break;
        …
        case Cx: ;
            break;
    }
}

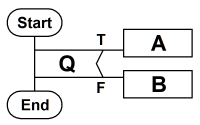
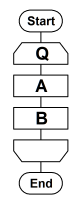
前判定反復

最初に条件「Q」を判定し、成立している間は処理「A」「B」を実行する例。「while文」に相当する。

PAD フローチャート フローチャート(JIS) サンプルコード
前判定反復(while loop)のPAD例 前判定反復(while loop)のフローチャート例 前判定反復(while loop)のフローチャート（JIS規格）例 
int sample(void)
{
    while(Q){
        A();
        B();
    }
}

後判定反復

処理「A」「B」を実行したあとに条件「Q」を判定し成立するまで処理を繰り返す例。「do-while文」に相当する。また、「for文」処理にも用いられる（条件設定部に初期値、継続条件、更新処理を記述する）。

PAD フローチャート フローチャート(JIS) サンプルコード
後判定反復(until loop)のPAD例 後判定反復(until loop)のフローチャート例 後判定反復(until loop)のフローチャート（JIS規格）例 
int sample(void)
{
    do{
        A();
        B();
    } while{Q};
}

拡張図式

連接、選択、反復の構造だけでは必ずしも全てのプログラムを実現できるわけではなく、例えば「goto文」を使うことが効率的なこともある。このような事例をPADで記述するための記法がある。また、ひとまとまりの処理を定義する記法もある。

N+1/2ループ

ループに入る前に行う処理がループ内でも行われる場合の記法である。標準記法でも記述できるが、拡張図式として記述することが出来る[8]。

PAD（標準図式） PAD（拡張図式） フローチャート サンプルコード
N＋1/2ループを表すPAD例（標準図式） N＋1/2ループを表すPAD例（拡張図式） N＋1/2ループを表すフローチャート例 
int sample(void)
{
    A();
    do{
        B();
        A();
    } while{Q};
}

Break

Break（gotoと同義）[9]。

PAD フローチャート サンプルコード
Break処理のPAD記載例 
    goto label;

label:

定義

処理（関数やサブルーチン）の定義名をつけて一連の処理を記述しておき、他のPAD図でその処理を引用する[10][11]。（以下の例では、処理名を「func」とし、定義名と処理の内容を「」でつなぐ。）

PAD フローチャート サンプルコード
PADによる定義済み処理の記載例

PADによる定義済み処理の記載例 

int func()
{
    A();
    while(P){
        if Q
            C();
        D();
    }
    B();
}

int sample(void)
{
    if (R)
        func();
    F();
}

実例

具体的な処理例として、打ち切り処理付きバブルソートのPAD、フローチャート、サンプルコードの対応を示す[注釈 1]。

PAD フローチャート サンプルコード
PADにバブルソート処理の記載例
  • break後に移行する場所を図中に記す「L1」
  • break記号内に移行場所「L1」を記す
 フローチャートによるバブルソート処理の記載例 
int bubblesort(int a[], int n)
{
    for (int i = 0; i < n-1; i++){
        int flag = 0;
        for (int j = n-1; j > i; j--)
            if (a[j-1] > a[j]){
                int work = a[j-1];
                a[j-1] = a[j];
                a[j] = work;
                flag = 1;
            }
        if (flag==0) break;
    }
}

PADの視覚的利点

PADによるプログラム構造の視覚効果
PADによるプログラム構造の視覚効果

PADでは、

  • 処理の実行順序 - 下への接続
  • 選択・反復の深さ - 右方向への展開

という2次元的な図になる。

これは、構造化プログラムにおいて、フローチャートでは判別しにくい論理構造がPADでは視覚的に把握しやすい図として表現できることを示している。同時に、処理の接続展開方向が規定されているので、プログラム構造を図にする場合はフローチャートに比べてPADで表記することで作成する個人差が出にくいという利点もある[13][14]。

逆に、プログラムの論理構造が明確でない場合はPADにすることができないともいえる[15][注釈 2]。

脚注

注釈

  1. ^ アルゴリズムは『新・明解 C言語で学ぶアルゴリズムとデータ構造』[12]を基にした。
  2. ^ 構造化されていないプログラムであるから、といえる[16]。

出典

  1. ^ a b 数値計算 2019, p. 25.
  2. ^ 情報処理学会論文誌1980 1980.
  3. ^ JISX0128 2008, pp. 3–6.
  4. ^ 情報処理学会論文誌1980 1980, pp. 259–260.
  5. ^ bit1980-03 1980, p. 16.
  6. ^ bit1980-03 1980, p. 20.
  7. ^ bit1980-03 1980, p. 21.
  8. ^ bit1980-04 1980, pp. 62–63.
  9. ^ bit1980-04 1980, pp. 63–65.
  10. ^ bit1980-04 1980, pp. 60–62.
  11. ^ 数値計算 2019, p. 29.
  12. ^ C言語で学ぶアルゴリズムとデータ構造 2021, pp. 214–215.
  13. ^ bit1980-03 1980, pp. 19–20.
  14. ^ 日立評論1980 1980, pp. 25–27.
  15. ^ bit1980-05 1980, p. 101.
  16. ^ 数値計算 2019, pp. 28–29.

参考文献

  • 川上一郎『数値計算』（新装版）岩波書店〈理工系の数学入門コース〉、2019年。ISBN 978-4-00-029890-2。 
  • 柴田望洋『新・明解 C言語で学ぶアルゴリズムとデータ構造』（第2版）SBクリエイティブ、2021年。ISBN 978-4-8156-0978-8。 
  • 二村良彦、川合敏雄、堀越彌、堤正義「PAD(Problem Analysis Diagram)によるプログラムの設計および作成」『情報処理学会論文誌』第21巻第4号、情報処理学会、1980年7月、NAID 110002723539。 
  • 二村良彦、川合敏雄「PADによるプログラムの開発」『bit』第12巻第4号、共立出版、1980年3月。 
  • 二村良彦、川合敏雄「PADによるプログラムの開発(2)」『bit』第12巻第5号、共立出版、1980年4月。 
  • 二村良彦、川合敏雄「PADによるプログラムの開発(3)」『bit』第12巻第6号、共立出版、1980年5月。 
  • 二村良彦、川合敏雄「プログラムの木構造化図面"PAD"」『日立評論』第62巻第12号、日立製作所、1980年12月、25-28頁。 
  • “JISX0128 プログラム構成要素及びその表記法”. 日本産業標準調査会 (1988年2月1日). 2022年4月10日閲覧。