折り紙公理

折り紙公理（おりがみこうり、折紙公理）は折り紙幾何学の一連の規則であり、紙を折るときに理論上厳密に可能である、基本的な操作を記述している[1]。紙の厚さは無いものとし、伸縮しないものとする[1]。折りの操作は平面で完結し、全ての折り線は直線であると仮定する[1]。折り紙公理は数学的な意味での公理の要件を満たすものではない^[要説明][1]。

公理は最初、1989年にジャック・ジュスタン (Jacques Justin) によって発見された[2]。その後公理1から6は藤田文章によって1991年に再度発見された[3]。また、公理7は羽鳥公士郎によって2001年に再発見された[4]。またロバート・J・ラングも公理7を再発見している。

7つの公理

公理1から6は藤田の折り紙公理として知られる。公理7は羽鳥公士郎によって再発見された。公理は以下である:

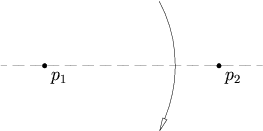
1. 2点p₁, p₂が与えられたとき、2点を通るただ1つの折り方がある。
2. 2点p₁, p₂が与えられたとき、p₁をp₂に重ねるただ1つの折り方がある。
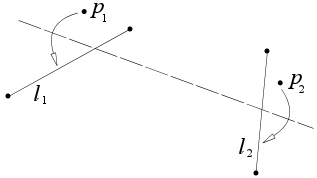
3. 2本の直線l₁, l₂が与えられたとき、l₁をl₂に重ねるような折り方がある。
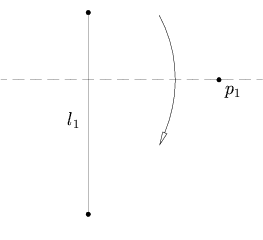
4. 1点p₁と1本の直線l₁が与えられたとき、l₁に垂直でp₁を通るただ1つの折り方がある。
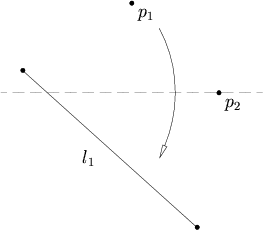
5. 2点p₁, p₂と1本の直線l₁が与えられたとき、p₁をl₁上に重ね、p₂を通る折り方がある。
6. 2点p₁, p₂2本の直線l₁, l₂が与えられたとき、p₁をl₁上に重ね、かつp₂をl₂上に重ねる折り方がある。
7. 1点pと2本の直線l₁, l₂が与えられたとき、pをl₁に重ね、l₂に垂直な折り方がある。

注目すべき点は、折り紙公理5は0, 1, 2個の解を持つ場合があり、公理6は0, 1, 2, 3個の解を持つ場合があることである。これにより最大の解が2個であるコンパスと定規の幾何学よりも強力な公理である。よってコンパスと定規の作図は2次方程式を解くことができるのに対し、折り紙の幾何学（オリガメトリー、origametry）では3次方程式や、角の三等分や立方体倍積などの問題を解くことができる。しかし、公理6の折り方を実際に行う際には、紙の"滑らせ"、言い換えるとネイシス (νευσις, neusis) を必要とする。これは古典的なコンパスと定規による作図では認められていないものである。コンパスと定規による作図にもネイシスを導入すれば、任意の角の三等分が可能となる。

詳細

公理 1

2点p₁, p₂が与えられたとき、2点を通るただ1つの折り方がある。

媒介変数表示では、この2点を通る折り線の直線の方程式は以下のように表せる。

${\displaystyle F(s)=p_{1}+s(p_{2}-p_{1})}$

公理 2

2点p₁, p₂が与えられたとき、p₁をp₂に重ねるただ1つの折り方がある。

この折り方は線分p₁p₂の垂直二等分線を求めていることに等しい。これは以下の4工程で折ることができる。

1. 公理1を用い、2点p₁, p₂を通る直線を求める。この直線は${\displaystyle P(s)=p_{1}+s(p_{2}-p_{1})}$と表される。
2. P(s)の中点p_midを求める。
3. P(s)に垂直なベクトルv^perpを求める。
4. よって媒介変数表示による折り線の方程式は以下のように表せる。

${\displaystyle F(s)=p_{\mathrm {mid} }+s\cdot {\boldsymbol {v}}^{\mathrm {perp} }}$

公理 3

2本の直線l₁, l₂が与えられたとき、l₁をl₂に重ねるような折り方がある。

これはl₁とl₂がつくる角の二等分線を求めていることに等しい。p₁とp₂をl₁上の任意の点とし、q₁とq₂をl₂上の任意の点とする。更にuとvをそれぞれl₁とl₂の単位方向ベクトルとすると、以下のように表される。

${\displaystyle {\boldsymbol {u}}=(p_{2}-p_{1})/\left|(p_{2}-p_{1})\right|}$

${\displaystyle {\boldsymbol {v}}=(q_{2}-q_{1})/\left|(q_{2}-q_{1})\right|}$

2直線が平行でないならば、2直線の交点は以下のように表せる。

${\displaystyle p_{\mathrm {int} }=p_{1}+s_{\mathrm {int} }\cdot {\boldsymbol {u}}}$

ここで

${\displaystyle s_{\mathrm {int} }=-{\frac {{\boldsymbol {v}}^{\perp }\cdot (p_{1}-q_{1})}{{\boldsymbol {v}}^{\perp }\cdot {\boldsymbol {u}}}}}$

二等分線の1つの方向は以下である。

${\displaystyle {\boldsymbol {w}}={\frac {\left|{\boldsymbol {u}}\right|{\boldsymbol {v}}+\left|{\boldsymbol {v}}\right|{\boldsymbol {u}}}{\left|{\boldsymbol {u}}\right|+\left|{\boldsymbol {v}}\right|}}}$

よって媒介変数表示による折り線の方程式は以下のように表せる。

${\displaystyle F(s)=p_{\mathrm {int} }+s\cdot {\boldsymbol {w}}}$

二等分線はもう1つあり、これは最初の二等分線に垂直でp_intを通るものである。このもう1つの二等分線でも、要求された条件「l₁をl₂に重ねる」を満たすことができる。交点の位置によってはどちらか片方の折り方をすることができない。

2直線が平行な場合、2直線は交点をもたない。このときの折り線はl₁とl₂の中間にある、l₁とl₂に平行な線となる。

公理 4

1点p₁と1本の直線l₁が与えられたとき、l₁に垂直でp₁を通るただ1つの折り方がある。

これはp₁を通るl₁の垂線を求めることに等しい。直線l₁に垂直なベクトルをvとするとき、媒介変数表示による折り線の方程式は以下で表せる。

${\displaystyle F(s)=p_{1}+s\cdot {\boldsymbol {v}}}$

公理 5

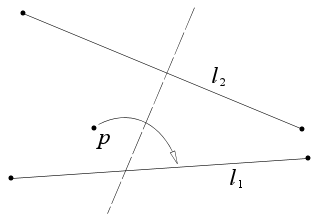
2点p₁, p₂と1本の直線l₁が与えられたとき、p₁をl₁上に重ね、p₂を通る折り方がある。

これは、p₂を中心としてp₁を通るような円と直線l₁との交点を求め、その交点にp₁を重ねる折り方である。一般に、直線と円との交点の個数は0, 1, 2個の場合があり、それに応じて、この公理による折り方がなかったり、1通りだったり、2通りあったりする。

直線上の2点(x₁, y₁), (x₂, y₂)がわかっている場合、直線は媒介変数によって以下で表される。

${\displaystyle x=x_{1}+s(x_{2}-x_{1})}$

${\displaystyle y=y_{1}+s(y_{2}-y_{1})}$

中心が${\displaystyle p_{2}=(x_{c},y_{c})}$で半径${\displaystyle r=\left|p_{1}-p_{2}\right|}$の円を定義する。この円の方程式は以下である。

${\displaystyle (x-x_{c})^{2}+(y-y_{c})^{2}=r^{2}}$

直線と円との交点を決定するために、円の方程式中のx, yを前述の直線の方程式で置き換え、以下を得る。

${\displaystyle (x_{1}+s(x_{2}-x_{1})-x_{c})^{2}+(y_{1}+s(y_{2}-y_{1})-y_{c})^{2}=r^{2}}$

これはsについての2次方程式であり、整理すれば次のように表せる。

${\displaystyle as^{2}+bs+c=0}$

ここで

${\displaystyle a=(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$

${\displaystyle b=2(x_{2}-x_{1})(x_{1}-x_{c})+2(y_{2}-y_{1})(y_{1}-y_{c})}$

${\displaystyle c=x_{c}^{2}+y_{c}^{2}+x_{1}^{2}+y_{1}^{2}-2(x_{c}x_{1}+y_{c}y_{1})-r^{2}}$。

この2次方程式の解を書き下すと次のようになる。

${\displaystyle {\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}$

判別式b^2 － 4ac < 0の場合、解はない。このとき円は線と交差したり接することがない。判別式が0に等しい場合、1つの解があり、このとき直線は円の接線となる。判別式が0より大きいとき、2つの解があり、このとき解は円と線の2つの交点として表される。解がある場合、この解をd₁, d₂とすると、以下の0, 1, 2本の線分を得る。

${\displaystyle m_{1}={\overline {p_{1}d_{1}}}}$

${\displaystyle m_{2}={\overline {p_{1}d_{2}}}}$

折り線F₁(s)はm₁の垂直二等分線で、p₁を直線上のd₁に重ねる。同様に、折り線F₂(s)はm₂の垂直二等分線で、p₂を直線上のd₂に重ねる。この折り方は公理2を応用することで容易に得ることができる。媒介変数表示による折り線の方程式は以下のように表せる。

${\displaystyle F_{1}(s)=p_{1}+{\frac {1}{2}}(d_{1}-p_{1})+s(d_{1}-p_{1})^{\perp }}$

${\displaystyle F_{2}(s)=p_{1}+{\frac {1}{2}}(d_{2}-p_{1})+s(d_{2}-p_{1})^{\perp }}$

公理 6

2点p₁, p₂2本の直線l₁, l₂が与えられたとき、p₁をl₁上に重ね、かつp₂をl₂上に重ねる折り方がある。

この公理は2つの抛物線の共通接線を求めることに等しく、3次方程式を解くことに等しいと見なせる。2つの抛物線はそれぞれp₁とp₂に焦点をもち、またl₁とl₂を準線とする。

公理 7

1点pと2本の直線l₁, l₂が与えられたとき、pをl₁に重ね、l₂に垂直な折り方がある。

羽鳥公士郎がこの公理を再発見し、ロバート・J・ラングがこれら7つの折り方で折り紙公理が完全であることを証明した。

参照文献

1. ^ 畠山, 一平『折紙数学－折紙で作図を楽しむ－』東京図書出版、2007年3月。ISBN 978-4-86223-166-6。 
2. Justin, Jacques, "Resolution par le pliage de l'equation du troisieme degre et applications geometriques", reprinted in Proceedings of the First International Meeting of Origami Science and Technology, H. Huzita ed. (1989), pp. 251–261.
3. Humiaki Huzita, “Understanding Geometry through Origami Axioms”, The First International Conference on Origami in Education and Therapy (COET91) (1991)
4. 日本折紙学会 Origami BBS (02021) 2001-06-28 15:37の発言

• 　ロベルト ゲレトシュレーガー 著、深川 英俊 訳『折紙の数学 ユークリッドの作図法を超えて』森北出版、2002年。ISBN 4627016816。 

• Origami Geometric Constructions （英語） by Thomas Hull
• A Mathematical Theory of Origami Constructions and Numbers （英語） by Roger C. Alperin
• ロバート・J・ラング (2003) (PDF). Origami and Geometric Constructions （英語）. ロバート・J・ラング. http://www.langorigami.com/science/hha/origami_constructions.pdf 2007年4月12日閲覧。. 
• 折り紙による作図 羽鳥公士郎による簡単な解説