多項式補間

多項式補間（たこうしきほかん、英: polynomial interpolation）は、数値解析において、与えられたデータ群を多項式で内挿（補間）することである。言い換えれば、標本調査などで得たデータ群について、それらを正確に通る多項式を見つけることである。

用途

多項式をより複雑な曲線の近似として使う場合もあり、タイポグラフィにおける文字の形状をいくつかの点で表すなどの例がある。関連する用途としては、自然対数や三角関数の値を求める際に、数表に掲載されている点から多項式補間で必要な値を求める場合がある。これは特定の値を直接求めようとするよりもかなり高速に計算できる。多項式補間はまた、数値積分や常微分方程式の数値解を求めるアルゴリズムの基盤にもなっている。

多項式補間は、Karatsuba法やToom-Cook法（英語版）といった乗算アルゴリズムの基盤であり、積を定義する多項式上の点間の補間が積自体を生成する。例えば a = f(x) = a₀x^0 + a₁x^1 + ... と b = g(x) = b₀x^0 + b₁x^1 + ... があるとき、積 ab は W(x) = f(x)g(x) と等しい。f(x) と g(x) が小さいときの x における W(x) 上の点を求めることで、その曲線上の点が得られる。それらの点に基づく補間によって W(x) の項とさらには積 ab が得られる。Karatsuba法の場合、穏当なサイズの入力であっても単純な乗算より高速である。特にハードウェアの並列性を利用するとその特性が発揮される。

定義

n+1 個のデータ点 (x_i,y_i) があり、x_i には同じ値のものがないとする。ここで、

${\displaystyle p(x_{i})=y_{i},\;i=0,\ldots ,n}$

という属性を持つ最大 n次の多項式を求める。unisolvence定理によれば、このような多項式 p は必ず存在し、一意に定まる。

より正確に言えば、その定理は n+1 個の補間ノード (x_i) について、多項式補間は次の線型全単射を定義する。

${\displaystyle L_{n}:\mathbb {K} ^{n+1}\to \Pi _{n}}$

ここで ${\displaystyle \Pi _{n}}$ は次数が n 以下の多項式のベクトル空間である。

補間多項式の構築

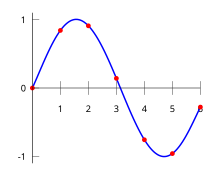
赤い点はデータ点 (x_k,y_k)T を表し、青い曲線は補間多項式を表している。

補間多項式が次のような形式であるとする。

${\displaystyle p(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{2}x^{2}+a_{1}x+a_{0}\qquad (1)}$

p がデータ点群を補間するとは、次を意味する。

${\displaystyle p(x_{i})=y_{i}\qquad {\mbox{for all }}i\in \left\{0,1,\dots ,n\right\}}$

ここで式 (1) に置換すると、係数 ${\displaystyle a_{k}}$ の線型方程式系が得られる。これを行列とベクトルで表すと次のようになる。

${\displaystyle {\begin{bmatrix}x_{0}^{n}&x_{0}^{n-1}&x_{0}^{n-2}&\ldots &x_{0}&1\\x_{1}^{n}&x_{1}^{n-1}&x_{1}^{n-2}&\ldots &x_{1}&1\\\vdots &\vdots &\vdots &&\vdots &\vdots \\x_{n}^{n}&x_{n}^{n-1}&x_{n}^{n-2}&\ldots &x_{n}&1\end{bmatrix}}{\begin{bmatrix}a_{n}\\a_{n-1}\\\vdots \\a_{0}\end{bmatrix}}={\begin{bmatrix}y_{0}\\y_{1}\\\vdots \\y_{n}\end{bmatrix}}}$

補間多項式 ${\displaystyle p(x)}$ を構築するには、この方程式系を ${\displaystyle a_{k}}$ について解かなければならない。

左辺の行列をファンデルモンド行列と呼ぶ。その行列式はゼロではなく、唯一の補間多項式が存在する。

ファンデルモンド行列の条件数は大きいため[1]、係数 ${\displaystyle a_{i}}$ を求めるのにガウスの消去法を使うと、大きな誤差を生じる。そのため、${\displaystyle {\mathcal {O}}(n^{3})}$ を要するガウスの消去法の代わりに、ファンデルモンド行列の特性を利用した ${\displaystyle {\mathcal {O}}(n^{2})}$ の数値的に安定な解法がいくつも提案されている[2][3][4]。これらの手法はまず多項式のニュートン補間を構築し、それを上掲のような単項形式に変換する。

ファンデルモンド以外の解法

ここで構築しようとしているのは、n次の多項式空間であるベクトル空間 ${\displaystyle \Pi _{n}}$ にある唯一の補間多項式である。${\displaystyle \Pi _{n}}$ の単項式基底（英語版）を用いると、ファンデルモンド行列を解いて補間多項式の係数群 ${\displaystyle a_{k}}$ を構築しなければならない。これは（コンピュータのクロック数で数えると）非常にコストがかかる操作である。${\displaystyle \Pi _{n}}$ の別の基底を選択すると係数の計算を単純化できるが、補間多項式を単項式基底で表現するために追加の計算が必要になる。

1つの手法として、補間多項式をニュートン補間形式で書き、差分商の手法で係数を構築する（これをネヴィル法（英語版）という）。そのコストは O${\displaystyle (n^{2})}$ で、一方ガウスの消去法のコストは O${\displaystyle (n^{3})}$ である。さらに、点が追加されたときそれまでの計算結果に若干加える形でよいという利点がある（他の手法では、全部の計算をやり直す必要がある）。

別の手法として、ラグランジュ補間形式の補間多項式を使う方法がある。得られる方程式から上の定義に指定されている条件に当てはまる補間多項式を即座に示すことができる。 多項式補間を行なうのに便利な方法として、重心形式補間法(barycentric interpolation)がある[5]。これは${\displaystyle n}$個の分点があらかじめ指定されているとき，補間1回あたり計算量${\displaystyle O(n)}$で関数の補間多項式の値が求まる。

ベルンシュテイン多項式（Bernstein polynomials）はセルゲイ・ベルンシュテインがワイエルシュトラスの近似定理の構築的証明に使ったが、現在ではコンピュータグラフィックスでよく使われるベジェ曲線の元になっている。(注：ベルンシュテイン多項式は、端点以外では分点上で関数値は一致しないので、「多項式補間」ではないが、次数を上げるとともに元の関数に区間内で一様に収束する多項式の列を与える近似法である。)

補間誤差

関数 f を x₀,...,x_n というノードを結ぶn次多項式で補間したとき、その誤差は以下のようになる。

${\displaystyle f(x)-p_{n}(x)=f[x_{0},\ldots ,x_{n},x]\prod _{i=0}^{n}(x-x_{i})}$

ここで

${\displaystyle f[x_{0},\ldots ,x_{n},x]}$

は差分商を表す。f がノード x_i と x を含む微小な区間 I において n+1 階連続微分可能ならば、I 上のある ${\displaystyle \xi }$ について誤差をラグランジュ形式で次のように書くことができる。

${\displaystyle f(x)-p_{n}(x)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}\prod _{i=0}^{n}(x-x_{i})}$

したがって、テイラーの定理のラグランジュ形式の剰余項は、全ての補間ノード x_i が同一であるような特殊ケースの補間誤差である。

${\displaystyle x_{i}=x_{0}+ih}$ のように等間隔な補間ノードの場合、補間誤差は O${\displaystyle (h^{n})}$ になる。しかし、このことから ${\displaystyle n\to \infty }$ となったときに何が起きるかはわからない。それについては後述の「収束属性」の節で扱う。

以上から、積 | ∏ (x − x_i) | を可能な限り小さくするような補間点 x_i の選択がありうることがわかる。これを達成しているのがチェビシェフノード（英語版）である。

ルベーグ定数

補間点 x₀, ..., x_n を設定し、全ての補間ノードが区間 [a, b] にあるとする。補間とはすなわち、関数 f から多項式 p への写像をする過程である。これにより、[a, b] 上の全ての連続関数の空間 C([a, b]) からそれ自身への写像 X を定義する。写像 X は線型であり、n次以下の多項式の部分空間 Π_n 上の射影である。

ルベーグ定数 L は X の作用素ノルムとして定義される。それは次のようになる（ルベーグの補題の特殊ケース）。

${\displaystyle \|f-X(f)\|\leq (L+1)\|f-p^{*}\|}$

言い換えれば、補間多項式は最良の近似に比べて最大で係数 (L+1) のぶんだけ悪い。従って補間ノード集合は L が小さいほどよいことを示唆している。特にチェビシェフノードは次のようになる。

${\displaystyle L\geq {\frac {2}{\pi }}\log(n+1)+C\quad {\mbox{for some constant }}C.}$

つまり、チェビシェフノードは多項式補間には最適の選択であり、同程度の良さを等間隔ノードで実現しようとすると n を指数関数的に成長させる必要がある。しかし、それらノードは最適ではない。

収束属性

補間多項式の次数 n を無限大に漸近させたとき、その一連の補間多項式が補間対象の関数に収束するような関数の種類や補間ノードのシーケンスはどのようなものだろうか? 収束は他にも、様々なノルムについて考えられる。

等間隔ノードでは状況は悪く、無限に微分可能な関数では一様収束も保証されない。カール・ルンゲの古典的例として、区間 [−5, 5] の関数 f(x) = 1 / (1 + x^2) がある。この場合、補間誤差 ||f − p_n||_∞ は n → ∞ に従って大きくなる。もう1つの例として、区間 [−1, 1] の関数 f(x) = |x| がある。この場合の補間多項式は x = −1, 0, 1 の3点以外では各点収束しない[6]。

補間ノードの選択によって収束属性がよくなるだろうか? 次の定理がある程度答になるだろう。

任意の関数 f(x) が区間 [a,b] 上で連続であるとき、一連の補間多項式 ${\displaystyle p_{n}(x)}$ が [a,b] 上で f(x) に一様に収束するようなノードの並びが存在する。

証明は次の通り。最良の近似の一連の多項式 ${\displaystyle p_{n}^{*}(x)}$ が f(x) に一様に収束することは明らかである（ワイエルシュトラスの近似定理より）。したがって、ここでは個々の ${\displaystyle p_{n}^{*}(x)}$ をあるノード群の補間によって得られることを示せばよい。しかし、チェビシェフの交替定理として知られる最良近似の多項式ではそれが真である。特に補間多項式は f(x) と少なくとも n+1 回交差する。交差点が補間ノードとなるよう選択すると、最良の近似多項式と同一の補間多項式が得られる。

しかしこの方法の欠陥は、関数 f(x) 毎に改めて補間ノードを計算しなければならず、しかもそのアルゴリズムは数値的に実装するのが難しい点である。どんな連続関数 f(x) についても一連の補間多項式が収束するようなノードの組合せがあるだろうか? 答は残念ながら次の定理で示される通り否定的である。

ノードの任意の組合せについて、区間 [a,b] において一連の補間多項式が発散するような連続関数 f(x) が存在する[7]。

その証明はルベーグ定数の下限推定を使うもので、それは上で定義したように X_n（すなわち Π_n 上の射影作用素）の作用素ノルムである。ここで、次のような性質のノードの組合せを探す。

${\displaystyle \lim _{n\to \infty }X_{n}f=f,}$ for any ${\displaystyle f\in C([a,b])}$

一様有界性原理（英語版）によると、X_n のノルムが一様有界であるときだけこのようなノード群が存在するが、${\displaystyle \|X_{n}\|\geq {\frac {2}{\pi }}\log(n+1)+C}$ であることから、そのようなノード群は存在しない。

例えば、等間隔点を補間ノードとして選択したとき、ルンゲ現象による発散が見られる。なお、その関数は単に連続であるだけでなく、区間 [−1, 1] において無限に微分可能である。チェビシェフノードより良い例は、次の定理により、見つけるのがさらに難しい。

区間 [−1, 1] で絶対連続なあらゆる関数について、チェビシェフノードで構築した一連の補間多項式は一様に f(x) に収束する。

関連する概念

ルンゲ現象とは、n が大きくなると補間多項式がデータ点間でより大きく振動するようになる現象である。この問題は一般にスプライン補間によって解決する。そのときの補間曲線は多項式ではなくスプライン曲線であり、低次のいくつかの多項式の連鎖になっている。

調和関数で周期関数を補間する場合、一般にフーリエ級数を用い、例えば離散フーリエ変換などで行っている。これは調和基底関数による多項式補間と見ることもできる。

エルミート補間（英語版）問題は、多項式 p の値が与えられるだけでなく、いくつかの導関数値も与えられる場合である。バーコフ補間は、それをさらに一般化し、p の値そのものは与えられず微分値だけを与えられる場合も含む。

微分方程式や積分方程式を解くコロケーション法（英語版）は、多項式補間に基づいている。

有理関数モデリングの技法は、多項式関数の比を考慮した一般化である。

脚注

1. Gautschi, Walter (1975). “Norm Estimates for Inverses of Vandermonde Matrices”. Numerische Mathematik 23: 337–347. doi:10.1007/BF01438260. 
2. Higham, N. J. (1988). “Fast Solution of Vandermonde-Like Systems Involving Orthogonal Polynomials”. IMA Journal of Numerical Analysis 8: 473–486. doi:10.1093/imanum/8.4.473. 
3. Björck, Å; V. Pereyra (1970). “Solution of Vandermonde Systems of Equations”. Mathematics of Computation 24 (112): 893–903. doi:10.2307/2004623. 
4. Calvetti, D and Reichel, L (1993). “Fast Inversion of Vanderomnde-Like Matrices Involving Orthogonal Polynomials”. BIT 33 (33): 473–484. doi:10.1007/BF01990529. 
5. Jean-Paul Berrut and Lloyd N. Trefethen: "Barycentric Lagrange Interpolation", SIAM Review, Vol.46, No.3, pp.501-517 (2004).
6. Watson (1980, p. 21) attributes the last example to Bernstein (1912).
7. Watson (1980, p. 21) attributes this theorem to Faber (1914).

参考文献

• Kendell A. Atkinson (1988). An Introduction to Numerical Analysis (2nd ed.), Chapter 3. John Wiley and Sons. ISBN 0-471-50023-2.
• Sergei N. Bernstein (1912), Sur l'ordre de la meilleure approximation des fonctions continues par les polynômes de degré donné. Mem. Acad. Roy. Belg. 4, 1–104.
• L. Brutman (1997), Lebesgue functions for polynomial interpolation — a survey, Ann. Numer. Math. 4, 111–127.
• Georg Faber (1912), Über die interpolatorische Darstellung stetiger Funktionen, Deutsche Math. Jahr. 23, 192–210.
• M.J.D. Powell (1981). Approximation Theory and Methods, Chapter 4. Cambridge University Press. ISBN 0-521-29514-9.
• Michelle Schatzman (2002). Numerical Analysis: A Mathematical Introduction, Chapter 4. Clarendon Press, Oxford. ISBN 0-19-850279-6.
• Endre Süli and David Mayers (2003). An Introduction to Numerical Analysis, Chapter 6. Cambridge University Press. ISBN 0-521-00794-1.
• G. Alistair Watson (1980). Approximation Theory and Numerical Methods. John Wiley. ISBN 0-471-27706-1.

外部リンク

• Interpolating Polynomial by Stephen Wolfram, The Wolfram Demonstrations Project.