 |
共焦点のその他の用法については「共焦点」をご覧ください。 |
| この項目「 共焦点円錐曲線」は翻訳されたばかりのものです。不自然あるいは曖昧な表現などが含まれる可能性があり、このままでは読みづらいかもしれません。(原文: Confocal conic sections oldid=1194929722)
修正、加筆に協力し、現在の表現をより自然な表現にして下さる方を求めています。 ノートページや 履歴も参照してください。 (2024年9月) |
 共焦点な円錐曲線の束。
共焦点な円錐曲線の束。
幾何学において、2つの円錐曲線が共焦点(きょうしょうてん、英: confocal)あるいは共焦であるとは、円錐曲線が焦点(focus;複数形はfoci)を共有している状態である。共焦点である円錐曲線は、共焦点円錐曲線、共焦点二次曲線、共焦円錐曲線、共焦二次曲線(confocal conics)などと言われる[1][2][3][4][5]。
楕円または双曲線は2つの焦点をもつため、共焦点楕円(confocal ellipses)、共焦点双曲線(confocal hyperbolas)あるいは、その混合物が存在する。共焦点である楕円と双曲線は直交する。
放物線は1つのみ焦点を持つため、共焦点放物線(confocal parabolas)は焦点と軸を共有する放物線であると定義される。 軸上にない任意の点はある共焦点放物線の交点となり、その共焦点放物線は直交する。
円は焦点がその中心に一致した楕円である。特別に、焦点(中心)を共有する円は同心であると言われる。また円の中心を通る直線と、円は直交する。
共焦点の概念を空間に一般化すれば、共焦点二次曲面(confocal quadrics)となる。
楕円と双曲線
任意の(円ではない)楕円または双曲線は、ユークリッド平面上に2つ異なるの焦点F1 , F2を持つ。また、長軸上にない点Pを与えれば、その点を通る楕円(または双曲線)は一意に決定される。焦点F1 , F2を共有し、Pを通る楕円と双曲線は直交する。
焦点をF1 , F2とする楕円と双曲線の束(共焦点有心円錐曲線族[6][7];Family of confocal central conics,Family of confocal centred conics;共焦点有心二次曲線[8])を作る。
主軸定理(英語版)より、直交座標系において、座標軸を軸、原点を焦点の中点(中心)とする円錐曲線を作ることができる。cを線型離心率 (焦点の距離の半分)としたとき、焦点の座標は となる。
となる。
 線型離心率をcとする共焦点円錐曲線の長軸aによる表示。 0 < a < cならば双曲線、c < aならば楕円となる。
線型離心率をcとする共焦点円錐曲線の長軸aによる表示。 0 < a < cならば双曲線、c < aならば楕円となる。
楕円と双曲線からなる共焦点円錐曲線は、次の等式を満たす点の軌跡となる。

ここで長軸の長さをaとした。 0 < a < cとなるようにaを決めれば双曲線、c < aとなるように定めれば楕円になる。
焦点の与えられた楕円、双曲線は、長軸と短軸の長さa,bによっても表すことができる(0 < b < a)。媒介変数λを用いて、次の式のようになる。

 ならば楕円、
ならば楕円、  ならば双曲線となる。
ならば双曲線となる。 ならば、解は実数上に存在しない。焦点の座標は
ならば、解は実数上に存在しない。焦点の座標は である。この表現方法は二次曲面の定義式に応用できる。
である。この表現方法は二次曲面の定義式に応用できる。
極限
媒介変数λがb2 に下から近づくと、楕円はx軸の焦点間の線分に退化(英語版)する。λがb2 に上から近づくと、双曲線が退化して、x軸の焦点の外側の部分になる。この性質もまた、3次元に応用できる。
直交
 反射の性質を用いた、楕円と双曲線の直交の視覚的な証明。
反射の性質を用いた、楕円と双曲線の直交の視覚的な証明。
共焦点な楕円、双曲線の束を考える。楕円の法線と双曲線の接線は、接点と焦点を繋ぐ2直線の角の二等分線になる。したがって図の様に、楕円と双曲線の直交を導ける。
このような楕円の束と双曲線の束のように、交差しない曲線の集合2つが、互いの要素に直交するような集合は、orthogonal netと呼ばれる。 楕円と双曲線のorthogonal netをもとにした楕円座標系(英語版)と呼ばれる座標系がある。
共焦点放物線
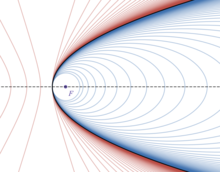 放物線は、一方の焦点を無限遠点に置いた、楕円または双曲線の特殊な場合とみることができる。
放物線は、一方の焦点を無限遠点に置いた、楕円または双曲線の特殊な場合とみることができる。
放物線は単一の焦点を持つ。これは、一方の焦点を固定して、もう一方の焦点を無限遠に移動させた場合の楕円または放物線と見なせる。楕円と双曲線の直交の性質を放物線に適用すれば、 ある放物線に直交する放物線は反対方向を向いた放物線になる。
焦点を原点、軸をx軸とした放物線は、次の式を満たす点の軌跡である。

媒介変数pについて、|p|はsemi-latus rectum(焦点を通る軸の垂線と放物線の交点を端とする線分長の半分)である。放物線は、 0 < pならば右側に開き、0 > pならば左に開く。 は頂点となる。
は頂点となる。
 共焦点放物線の束。
共焦点放物線の束。
放物線の定義式より、x軸上にない任意の点 について、焦点と軸をそれぞれ原点、x軸とする放物線は、右に開いたものと左に開いたものが一つずつ存在する。また、これらは直交する。
について、焦点と軸をそれぞれ原点、x軸とする放物線は、右に開いたものと左に開いたものが一つずつ存在する。また、これらは直交する。
共焦点な楕円と双曲線によって、楕円座標系が作られるのと同様に、共焦点放物線の束は放物座標系(英語版)の基底となる。
等角写像 によって共焦点放物線のnetは、座標軸に平行な直線の像と、複素平面の右半分と見なせる(外部リンク参照)。
によって共焦点放物線のnetは、座標軸に平行な直線の像と、複素平面の右半分と見なせる(外部リンク参照)。
同心円
円は二つの焦点を一致させた楕円である。一方、焦点を一致させた双曲線は、その点を通る2直線に退化する。
したがって共焦点な楕円と双曲線によってもたらされたorthogonal netは、同心円とその中心を通る直線になる。これは極座標系の基底となる。
焦点を反対方向に無限遠まで離すと楕円は長軸に平行な2直線に退化し、双曲線は長軸に垂直な2直線に退化する。したがって、直交する網は共焦点円錐曲線の束であるとみなせる。このようにして特に直交座標系を作ることができる。
グレイヴスの定理
 共焦点楕円の構築
共焦点楕円の構築
1850年、アイルランドの司祭チャールズ・グレイヴス(英語版)は、糸を用いた共焦点楕円の作成方法を発表した[10]。
- 周長よりも長い糸を楕円Eにまきつける。ある点に糸を掛けて、糸が張るような点の集合はEと共焦点な楕円となる。
フェリックス・クラインの書籍で示された証明は楕円積分を用いる。Otto Staudeは同様の方法を楕円体へ拡張した(クラインの書籍を見よ)。
楕円Eが線分F1F2に退化するときは、糸で楕円を描く特殊な場合になる。
二次曲面
 共焦点二次曲面
共焦点二次曲面

 (赤),
(赤), (青),
(青),  (紫)
(紫)

 の値と曲面の関係
の値と曲面の関係
2つの二次曲面が共焦点であるとは、軸を共有し、平面との交面が共焦点楕円になっている状態を指す。円錐曲線の場合に類推して、非退化な共焦点二次曲面の束は3軸楕円体、一葉双曲面 と二葉双曲面、楕円放物面、双曲放物面、双方向に開いた楕円放物面の2種類がある。
3軸の長さの半分を (
( )とする3軸楕円体は共焦点二次曲面の束を決定する。変数
)とする3軸楕円体は共焦点二次曲面の束を決定する。変数 で作られたそれぞれの二次曲面は、次の式を満たす点の集合となる。
で作られたそれぞれの二次曲面は、次の式を満たす点の集合となる。

 ならば楕円体、
ならば楕円体、 ならば一葉双曲面、
ならば一葉双曲面、 ならば二葉双曲面となり、
ならば二葉双曲面となり、  ならば解は存在しない。
ならば解は存在しない。
焦点曲線
 焦点円錐曲線(黒い楕円、放物線)
焦点円錐曲線(黒い楕円、放物線)



 (楕円体、赤)、
(楕円体、赤)、  (一葉双曲面、青)、
(一葉双曲面、青)、  (一葉双曲面、青),
(一葉双曲面、青),  (ニ葉双曲面、紫)下部は極限の場合。
(ニ葉双曲面、紫)下部は極限の場合。
極限:
 が
が に下から近づくと、楕円体は次の式で示されるx-y平面の楕円に退化する(図左上の赤い部分)。
に下から近づくと、楕円体は次の式で示されるx-y平面の楕円に退化する(図左上の赤い部分)。

 が
が に上から近づくと、一葉双曲面はx-y平面の楕円
に上から近づくと、一葉双曲面はx-y平面の楕円 の外側の部分に退化する(図左下、青い部分)。
の外側の部分に退化する(図左下、青い部分)。
どちらの極限の場合も 上に点を持つ。
上に点を持つ。
極限: 
同様に  が上下から
が上下から  に近づくと、それぞれの双曲面の極限の面(図右下、青と紫)は、共通の双曲線
に近づくと、それぞれの双曲面の極限の面(図右下、青と紫)は、共通の双曲線

を持つ。
焦点曲線
 の焦点は
の焦点は の頂点である。逆もまた然り。したがって、
の頂点である。逆もまた然り。したがって、 と
と は焦点円錐曲線(英語版)の組である。
は焦点円錐曲線(英語版)の組である。
逆に、共焦点二次曲面の束の任意の二次曲面はピンと糸の方法によって構築できる。この際、焦点円錐曲線 は無数の焦点の役割を果たし、束の焦点曲線(focal curves)と呼ばれる[11][12][13]。
は無数の焦点の役割を果たし、束の焦点曲線(focal curves)と呼ばれる[11][12][13]。
直交系
共焦点楕円、双曲線から類推して、
- 任意の点
 (ただし
(ただし  )は3種類の共焦点二次曲面のいずれかひとつ上に存在する。
)は3種類の共焦点二次曲面のいずれかひとつ上に存在する。
 を通る3つの二次曲面は垂直に交わる(外部リンクを参照)。
を通る3つの二次曲面は垂直に交わる(外部リンクを参照)。

 の例
の例
・点を通る3つの二次曲面が一意に存在する証明 で点
で点  について、関数
について、関数 を定める。この関数は3つの直交する漸近線
を定める。この関数は3つの直交する漸近線 を持ち、区間
を持ち、区間 の中で、連続で単調増加な関数である。垂直な漸近線付近での振る舞いと
の中で、連続で単調増加な関数である。垂直な漸近線付近での振る舞いと から次のことが分かる。
から次のことが分かる。 は3つの根
は3つの根 (
( )を持つ。
)を持つ。
・面の直交の証明
 の束を用いて、共焦点二次曲面は
の束を用いて、共焦点二次曲面は と書ける。交差する2つの二次曲面
と書ける。交差する2つの二次曲面 について、共通の点
について、共通の点 をとる。
をとる。


この方程式より、共通の点における勾配のスカラー積を得る。

よって題意は示された。
 共焦点双曲面
共焦点双曲面 との交線に曲率線を持つ楕円体。
との交線に曲率線を持つ楕円体。
応用
デュパンの定理(英語版)より、任意の2つの二次曲面の交線は曲率線となる[14]。楕円座標系(英語版)から類推して、これは楕円体座標系(英語版)の基底となる。
物理学において、共焦点楕円体は帯電した楕円体の等位面(英語版)として現れる[15][16]。
アイヴォリーの定理
 アイボリーの定理
アイボリーの定理
アイヴォリーの定理[7](Ivory's theorem)またはアイヴォリーの補題は、スコットランドの数学者ジェームズ・アイヴォリーに因んだ、直交する曲線が成す四角形(net-rectangle)の対角線に関する定理である。
- それぞれ2つの共焦点楕円、双曲線の成す任意のnet-rectangleについて、2つの対角線の長さは等しい。
 を、焦点が
を、焦点が である次の式で表される楕円とする。
である次の式で表される楕円とする。

また、 を次の式で表される楕円と共焦点な双曲線とする。
を次の式で表される楕円と共焦点な双曲線とする。

 と
と  の4交点を計算する。
の4交点を計算する。

 としても一般性を失わない(cを変えると原点中心に相似拡大される)。4交点の中から第一象限にある物を選ぶ。
としても一般性を失わない(cを変えると原点中心に相似拡大される)。4交点の中から第一象限にある物を選ぶ。
4つの曲線が焦点を共有するように、 を二つの共焦点楕円、
を二つの共焦点楕円、 を二つの共焦点双曲線として、net-rectangle の頂点と対角線の長さを次のように得る。
を二つの共焦点双曲線として、net-rectangle の頂点と対角線の長さを次のように得る。
![{\displaystyle {\begin{aligned}P_{11}&=\left(a_{1}u_{1},\;{\sqrt {(a_{1}^{2}-1)(1-u_{1}^{2})}}\right),&P_{22}&=\left(a_{2}u_{2},\;{\sqrt {(a_{2}^{2}-1)(1-u_{2}^{2})}}\right),\\[5mu]P_{12}&=\left(a_{1}u_{2},\;{\sqrt {(a_{1}^{2}-1)(1-u_{2}^{2})}}\right),&P_{21}&=\left(a_{2}u_{1},\;{\sqrt {(a_{2}^{2}-1)(1-u_{1}^{2})}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd5dee278f31e26ceaf9f323bce7bbdc764480b9)
![{\displaystyle {\begin{aligned}|P_{11}P_{22}|^{2}&=(a_{2}u_{2}-a_{1}u_{1})^{2}+\left({\sqrt {(a_{2}^{2}-1)(1-u_{2}^{2})}}-{\sqrt {(a_{1}^{2}-1)(1-u_{1}^{2})}}\right)^{2}\\[5mu]&=a_{1}^{2}+a_{2}^{2}+u_{1}^{2}+u_{2}^{2}-2\left(1+a_{1}a_{2}u_{1}u_{2}+{\sqrt {(a_{1}^{2}-1)(a_{2}^{2}-1)(1-u_{1}^{2})(1-u_{2}^{2})}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/115d7ba18ca8d9155df57ee3dfca0f524a61403e)
最後の辺において、 としても値は変化しない。つまり
としても値は変化しない。つまり  の赤黒を入れ替えても値は変化しないから、
の赤黒を入れ替えても値は変化しないから、  を得る。
を得る。
共焦点放物線については、より簡単な計算で証明できる。
アイヴォリーは3次元への一般化を示した (s. Blaschke, p. 111)。
- 三次元において、共焦点二次曲面からなる直方体の対角線の長さは等しい。
関連項目
出典
- ^ 西内貞吉、柏木秀利『最新解析幾何学』成象堂、1925年、278頁。NDLJP:942895。
- ^ Eugène Rouché,Charles de Comberousse 著、小倉金之助 訳『初等幾何學 第2卷 空間之部』山海堂書店、1915年、521頁。doi:10.11501/1082037。
- ^ ジョン・ケージー 著、山下安太郎, 高橋三蔵 訳『幾何学続編』有朋堂、1909年。doi:10.11501/828521。
- ^ 森本清吾『解析幾何学』高岡本店、1934年、127頁。NDLJP:1233324。
- ^ サーモン 著、小倉金之助 訳『解析幾何学 : 円錐曲線』山海堂、1914年、314頁。doi:10.11501/952208。
- ^ 日本數學會『岩波數學辭典』岩波書店、1954年。https://www.google.co.jp/books/edition/%E5%B2%A9%E6%B3%A2%E6%95%B8%E5%AD%B8%E8%BE%AD%E5%85%B8/LP05AAAAMAAJ。
- ^ a b 『新訂版 数学用語 英和辞典: 和英索引付き』近代科学社、2020年12月2日。ISBN 978-4-7649-0624-2。https://www.google.co.jp/books/edition/%E6%96%B0%E8%A8%82%E7%89%88_%E6%95%B0%E5%AD%A6%E7%94%A8%E8%AA%9E_%E8%8B%B1%E5%92%8C%E8%BE%9E%E5%85%B8/SHMNEAAAQBAJ。
- ^ 竹内端三『函数概論』共立出版、1946年、60頁。NDLJP:1063358。
- ^ Felix Klein: Vorlesungen über Höhere Geometrie, Sringer-Verlag, Berlin, 1926, S.32.
- ^ Staude, O.: Ueber Fadenconstructionen des Ellipsoides. Math. Ann. 20, 147–184 (1882)
- ^ Staude, O.: Ueber neue Focaleigenschaften der Flächen 2. Grades. Math. Ann. 27, 253–271 (1886).
- ^ Staude, O.: Die algebraischen Grundlagen der Focaleigenschaften der Flächen 2. Ordnung Math. Ann. 50, 398 – 428 (1898)
- ^ 窪田 忠彦『高等数学叢書 第7 微分幾何学』岩波書店、1940年、175頁。NDLJP:1172588。
- ^ D. Fuchs, S. Tabachnikov: Ein Schaubild der Mathematik. Springer-Verlag, Berlin/Heidelberg 2011, ISBN 978-3-642-12959-9, p. 480.
- ^ 竹内時男『応用函数論階梯』有隣堂出版、1948年、60頁。NDLJP:1063359。
- Blaschke, Wilhelm「VI. Konfokale Quadriken [Confocal Quadrics]」『Analytische Geometrie [Analytic Geometry]』Springer、Basel、1954年、108–132頁。https://archive.org/details/analytischegeome0000wilh/page/108。
- Glaeser, Georg; Stachel, Hellmuth; Odehnal, Boris (2016). “2. Euclidean Plane”. The Universe of Conics. Springer. pp. 11–60. doi:10.1007/978-3-662-45450-3_2. ISBN 978-3-662-45449-7 See also "10. Other Geometries", doi:10.1007/978-3-662-45450-3_10.
- Hilbert, David; Cohn-Vossen, Stephan (1952), “§1.4 The Thread Construction of the Ellipsoid, and Confocal Quadrics”, Geometry and the Imagination, Chelsea, pp. 19–25, https://archive.org/details/geometryimaginat0000dhil/page/19
- Odehnal, Boris; Stachel, Hellmuth; Glaeser, Georg (2020). “7. Confocal Quadrics”. The Universe of Quadrics. Springer. pp. 279–325. doi:10.1007/978-3-662-61053-4_7. ISBN 978-3-662-61052-7
- Ernesto Pascal: Repertorium der höheren Mathematik. Teubner, Leipzig/Berlin 1910, p. 257.
- A. Robson: An Introduction to Analytical Geometry Vo. I, Cambridge, University Press, 1940, p. 157.
- Sommerville, Duncan MacLaren Young「XII. Foci and Focal Properties」『Analytical Geometry of Three Dimensions』Cambridge University Press、1934年、224–250頁。https://archive.org/details/analyticalgeomet0000somm/page/224/。
外部リンク













































































![{\displaystyle {\begin{aligned}P_{11}&=\left(a_{1}u_{1},\;{\sqrt {(a_{1}^{2}-1)(1-u_{1}^{2})}}\right),&P_{22}&=\left(a_{2}u_{2},\;{\sqrt {(a_{2}^{2}-1)(1-u_{2}^{2})}}\right),\\[5mu]P_{12}&=\left(a_{1}u_{2},\;{\sqrt {(a_{1}^{2}-1)(1-u_{2}^{2})}}\right),&P_{21}&=\left(a_{2}u_{1},\;{\sqrt {(a_{2}^{2}-1)(1-u_{1}^{2})}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd5dee278f31e26ceaf9f323bce7bbdc764480b9)
![{\displaystyle {\begin{aligned}|P_{11}P_{22}|^{2}&=(a_{2}u_{2}-a_{1}u_{1})^{2}+\left({\sqrt {(a_{2}^{2}-1)(1-u_{2}^{2})}}-{\sqrt {(a_{1}^{2}-1)(1-u_{1}^{2})}}\right)^{2}\\[5mu]&=a_{1}^{2}+a_{2}^{2}+u_{1}^{2}+u_{2}^{2}-2\left(1+a_{1}a_{2}u_{1}u_{2}+{\sqrt {(a_{1}^{2}-1)(a_{2}^{2}-1)(1-u_{1}^{2})(1-u_{2}^{2})}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/115d7ba18ca8d9155df57ee3dfca0f524a61403e)


