|
インボリュート歯車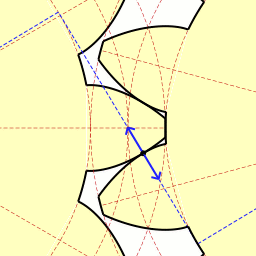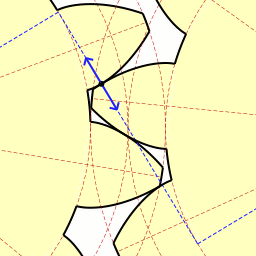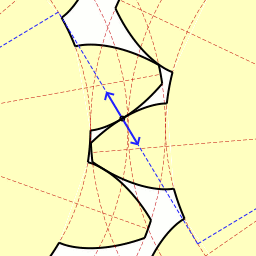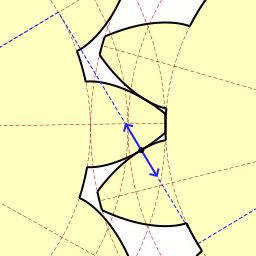 インボリュート歯車は、歯車、特に平歯車および斜歯(はすば)歯車において、歯の軸と直交する断面の形状をインボリュート曲線としたもので、いくつかの良い特性があることから、近年では他の曲線の歯車に比べ機械製品で最も多く使われる。レオンハルト・オイラーの発案による[1] 。 設計上の各部の名称 歯形となるインボリュート曲線の元となる円を基礎円と呼ぶ。2枚の歯車のそれぞれの基礎円(右図 base circle 1 および 2)の両方に接する4本の線のうち、交差する2本の一方を作用線(同 line of action)と呼ぶ。双方の歯はそれぞれインボリュート曲線(同 s1 および s2)であり、その接する点は回転が進んでも必ず作用線上になる。そして2つのインボリュート曲線の共通接線(同 T)と作用線は直交する。この作用線と両基礎円の中心(同 O1 および O2)を結ぶ線との交点をピッチ点 (同 P) と呼び、各基礎円の中心から半径がピッチ点までの円をピッチ円(同 pitch circle 1 および 2)と呼ぶ。両ピッチ円の共通接線と作用線の成す角を圧力角(同 alpha)と呼ぶ。 回転比の設計2枚の歯車のピッチ円の直径をそれぞれ d1、d2、基礎円の直径を dg1、dg2、中心間距離を a とすると、 cos(alpha) = dg1/d1 = dg2/d2 = (dg1+dg2)/(d1+d2) = (dg1+dg2)/a が成立する。つまり圧力角は歯車の軸間距離が変わると変化するが、回転にともなって変化することはない。  基礎円周上での各歯のインボリュート曲線の出発点の間隔を、基礎円ピッチと呼ぶ。これがかみ合う2枚の歯車で共通であることで、かみ合いが連続して生じ円滑に回転が伝達される。基礎円ピッチは円周長を歯の枚数で除した値であり、これは右図の te と等しくなる。この te を法線ピッチ(normal pitch)と呼ぶ。2枚の歯車の歯の枚数をそれぞれ z1、z2 とすると、 a1a2=a2a3=... = pi dg1/z1 = pi dg2 / z2 = te となる。歯数の比とピッチ円直径の比は等しくなるようにすると、回転数(角速度)の比 rは r = d1/d2 = dg1/dg2 = z1/z2 となる。つまり歯車の軸間距離 a とは無関係になり、基礎円あるいはピッチ円の直径の比で決まることになる。 かみ合い率法線ピッチを短くして歯数を増やすと、同時にかみあう歯の数が増える。これにより回転の伝達が円滑になり、また歯にかかる力が小さくなる。一組の歯の接触点の軌跡を接触弧と呼び、ピッチ円周上の歯のピッチである円ピッチで接触弧の長さを除した値をかみ合い率と呼ぶ。インボリュート歯車においては接触点は作用線という直線上を動くため、作用線上での接触している点の移動距離を法線ピッチで除した値になる。 実際に接触が開始、終了する点の位置は、歯先円の直径によって決まる。歯先円が作用線と交わる点が接触の開始および終了点であり、この間の長さをかみ合い長さと呼ぶ。これを法線ピッチで除した値がかみ合い率である。かみ合い率が 1 であれば、法線ピッチとかみ合い長さが同じということであり、ある歯が接触を終了すると同時に次の歯が接触を始める。2 であれば接触を始めた歯がピッチ点に達した時に次の歯が接触を始め、最初の歯が接触を終了する時に次の歯がピッチ点に達しさらに次の歯が接触を始める。かみ合い率が 2 以上になるとかみ合いの開始、終了に伴うトルクの変化や騒音の発生が非常に小さくなる。 歯面の摩擦歯がかみ合って回転を伝える際には、転がり接触をするのが理想であるが、インボリュート歯車では少ないながらも接触する歯面の間に滑りが生じる。滑りの際の摩擦力は、ピッチ点の手前では回転を妨げるが、ピッチ点の後ではむしろ回転の伝達を助ける。この滑る距離は、双方のピッチ円半径、歯数の比および圧力角によって変わる。またピッチ円から外周側(歯末)と内周側(歯元)でも異なる。圧力角が小さくなると滑りが大きくなり、ピッチ点の手前では歯元の方が滑りが大きい。 歯車の動力伝達の際の効率は、この滑りの量と、かみ合い率でほぼ決定される。かみ合い率が高いことは接触点が多く摩擦面が多いことになるが、両方の歯車でのかみ合い率の値を近くすることで効率はよくなる。 実際の設計圧力角を大きくすることで伝達可能なトルクを大きくすることができ、小さくすることでバックラッシを小さくし、伝達をより円滑にし、また工作精度を下げることができる[2]が、実際には 20° とするものが多い[3]。
斜歯のインボリュート歯車は、作用線が二つの基礎円の交差しない共通接線になり[5][6]、また滑りも大きいため[7][8]、使われることは少ない。 脚注
参考文献
|