Tangente alla circonferenza

In geometria euclidea si chiama tangente ad circonferenza ${\displaystyle \Gamma }$ una retta ${\displaystyle t}$ che tocca ${\displaystyle \Gamma }$ in un solo punto. È possibile dimostrare che preso un punto ${\displaystyle A}$ non esistono tangenti se ${\displaystyle A}$ è interno a ${\displaystyle \Gamma }$, vi è esattamente una tangente se ${\displaystyle A}$ è un punto di ${\displaystyle \Gamma }$ e vi sono esattamente due tangenti distinte se ${\displaystyle A}$ è esterno a ${\displaystyle \Gamma }$.

Costruzione tangenti da un punto esterno

Dato un punto ${\displaystyle P}$ esterno alla circonferenza ${\displaystyle \Gamma }$ è possibile costruire le tangenti a tale circonferenza per ${\displaystyle P}$ (e quindi dimostrare l'esistenza di tali rette tangenti).

Metodo di Euclide

Euclide propone una costruzione di tali tangenti negli Elementi (Libro III - Proposizione 17).

Dal centro ${\displaystyle O}$ della circonferenza ${\displaystyle \Gamma }$ si tracci il segmento ${\displaystyle {\overline {OA}}}$ e si disegni la circonferenza ${\displaystyle \Gamma '}$ di centro ${\displaystyle O}$ e raggio ${\displaystyle {\overline {OA}}}$.

Sia ${\displaystyle B}$ uno dei due punti di intersezione tra ${\displaystyle \Gamma }$ e ${\displaystyle {\overline {OA}}}$ (scegliamo ad esempio quello tra ${\displaystyle O}$ ed ${\displaystyle A}$).

Da tale punto ${\displaystyle B}$ si tracci la perpendicolare a ${\displaystyle {\overline {OA}}}$ e sia ${\displaystyle D}$ uno dei due punti di intersezione di tale perpendicolare con la circonferenza ${\displaystyle \Gamma '}$.

Si tracci ${\displaystyle {\overline {OD}}}$ e si indichi con ${\displaystyle E}$ il punto di intersezione tra ${\displaystyle {\overline {OD}}}$ e ${\displaystyle \Gamma }$.

La retta ${\displaystyle {\overline {EA}}}$ è una delle due tangenti a ${\displaystyle \Gamma }$ per il punto esterno ${\displaystyle A}$.

Elementi di Euclide - Libro III - Proposizione 17 (costruzione delle tangenti ad una circonferenza da un punto esterno ad essa)

Infatti, ${\displaystyle {\overline {OA}}={\overline {OD}}}$ poiché entrambi raggi di ${\displaystyle \Gamma '}$ ed ${\displaystyle {\overline {OB}}={\overline {OE}}}$ poiché entrambi raggi di ${\displaystyle \Gamma }$.

I triangoli ${\displaystyle EOA}$ e ${\displaystyle BOD}$ sono congruenti poiché hanno due lati e l'angolo compreso tra questi congruenti.

Quindi, in particolare l'angolo ${\displaystyle OEA=OBD}$ è retto.

Per la proposizione degli Elementi 3.16, una retta che formi un angolo retto con un diametro (in questo caso con ${\displaystyle {\overline {OE}}}$) è tangente alla circonferenza. Da cui la tangenza di ${\displaystyle {\overline {EA}}}$ a ${\displaystyle \Gamma }$.

L'altra tangente si costruisce scegliendo l'altro dei due punti di intersezione della perpendicolare a ${\displaystyle {\overline {OA}}}$ con la circonferenza ${\displaystyle \Gamma '}$.

Metodo alternativo

Si congiunga P con il centro ${\displaystyle O}$ della circonferenza ${\displaystyle \Gamma }$ e si tracci ${\displaystyle M}$ il punto medio del segmento ${\displaystyle {\overline {PO}}}$.

Si disegni la circonferenza di centro M e raggio ${\displaystyle {\overline {MP}}}$ e si indichino con ${\displaystyle T_{1}}$ e ${\displaystyle T_{2}}$ i punti di intersezione di tale circonferenza con ${\displaystyle \Gamma }$.

Le rette ${\displaystyle {\overline {PT_{1}}}}$ e ${\displaystyle {\overline {PT_{2}}}}$ sono le tangenti alla circonferenza ${\displaystyle \Gamma }$ condotte dal punto 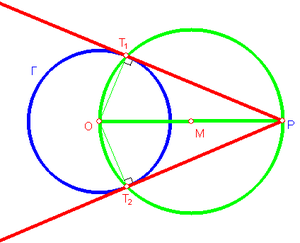${\displaystyle P}$.

Costruzione delle tangenti ad una circonferenza da un punto esterno ad essa

Infatti, i due triangoli ${\displaystyle OT_{1}P}$ e ${\displaystyle OT_{2}P}$ sono rettangoli in ${\displaystyle T_{1}}$ e ${\displaystyle T_{2}}$ rispettivamente poiché inscritti in semicirconferenze; quindi ${\displaystyle {\overline {PT_{1}}}}$ e ${\displaystyle {\overline {PT_{2}}}}$ sono le tangenti alla circonferenza ${\displaystyle \Gamma }$ condotte da ${\displaystyle P}$ poiché perpendicolare ai raggi ${\displaystyle OT_{1}}$ ${\displaystyle OT_{2}}$ rispettivamente.

Calcoli e grafica al P.C.

Elaborati in Visual Basic

Tangente nella geometria cartesiana

In geometria cartesiana il coefficiente angolare della tangente si trova calcolando la derivata totale dell'equazione della circonferenza rispetto ad ${\displaystyle x}$ o ${\displaystyle y}$, applicata nel punto interessato sulla circonferenza.

Collegamenti esterni

• (EN) Eric W. Weisstein, Tangente alla circonferenza, su MathWorld, Wolfram Research.