Risonanza Schumann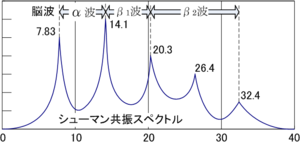

Riproduzione animata non in scala della risonanza di Schumann.

La risonanza Schumann è un gruppo di picchi di risonanza avvertibili nella porzione di spettro elettromagnetico nelle frequenze estremamente basse (ELF), presenti nella atmosfera terrestre. Si tratta di risonanze elettromagnetiche globali, eccitate dalle scariche elettriche dei fulmini, nella cavità formata tra la superficie terrestre e la ionosfera. Questo fenomeno prende il nome dal fisico tedesco Winfried Otto Schumann, che nel 1952 ne scrisse una previsione matematica.

Storia

I primi avvisi dell'esistenza di una ionosfera, capace di intrappolare le onde elettromagnetiche, fu fatta da Oliver Heaviside e Kennelly nel 1902[1][2]. Ci vollero altri venti anni prima che Edward Appleton e Barnett nel 1925[3], fossero in grado di provare sperimentalmente l'esistenza della ionosfera. Tuttavia, anche prima di questo, le prime osservazioni documentate delle risonanze elettromagnetiche globali furono fatte da Nikola Tesla nel 1905[4][5] e formarono la base del suo schema per la trasmissione energetica senza fili.[6] Anche se alcuni dei più importanti strumenti matematici per affrontare le guide d'onda sferiche furono sviluppati da Watson nel 1918[7], fu Winfried Otto Schumann che studiò per primo gli aspetti teorici della risonanza globale del sistema di guida d'onda tra terra e ionosfera. Tra il 1952 e il 1954 Schumann, assieme a Köning, tentò di misurare le frequenze risonanti[8][9][10][11]. Tuttavia non fu possibile fino alle misure fatte da Balser e Wagner nel 1960-1963[12][13][14][15][16], in cui furono disponibili tecniche di analisi adeguate all'estrazione dell'informazione della risonanza dal rumore di fondo. Da allora c'è stato un sempre più grande interesse nelle risonanze di Schumann in un'ampia varietà di campi.

Descrizione

La risonanza di Schumann avviene perché lo spazio atmosferico tra la superficie della Terra e la ionosfera conduttiva, agisce come una guida d'onda di dimensioni limitate, facendola comportare come una cavità di risonanza per le onde elettromagnetiche nella banda ELF (con lunghezza d'onda di svariati kilometri). La cavità è naturalmente eccitata dall'energia delle scariche dei fulmini. Le risonanze di Schumann sono osservabili nello spettro di potenza del rumore elettromagnetico naturale di fondo, come picchi separati nelle frequenze estremamente basse (ELF) attorno alla fondamentale di 7,83 Hz e alle seguenti armoniche 14,3 - 20,8 - 27,3 - 33,8 Hz.

Spettro tipico delle oscillazioni elettromagnetiche di frequenza ultrabassa con risonanze di Schumann. Il picco caratteristico alla frequenza di 50 Hz è dovuto alle fluttuazioni della frequenza industriale euro-asiatica. L'aumento della caratteristica nella regione della frequenza zero è causato da processi che scorrono lentamente nella magnetosfera terrestre.

La frequenza fondamentale delle risonanze di Schumann è un'onda stazionaria nella cavità Terra-ionosfera con una lunghezza d'onda uguale alla circonferenza della Terra. Questa frequenza fondamentale più bassa (e di maggiore intensità) della risonanza di Schumann è pari a circa 7,83 Hz, tuttavia può variare a causa di svariati fattori, come le perturbazioni della ionosfera indotte dal Sole, che comprimono la parete superiore della cavità. Le frequenze superiori sono divise da intervalli di circa 6,5 Hz, caratteristica che viene attribuita alla geometria sferica dell'atmosfera. L'ottavo ipertono si colloca a circa 60 Hz.

Le risonanze di Schumann vengono utilizzate per tracciare l'attività globale dei fulmini. A causa della connessione tra l'attività dei fulmini e il clima terrestre, queste possono anche essere usate per monitorare le variazioni della temperatura globale e del vapore acqueo presente nell'atmosfera. Con le risonanze di Schumann potrebbero essere rilevati e studiati anche i fulmini extraterrestri. La risonanza di Schumann è stata usata per la ricerca e il controllo della bassa ionosfera sulla Terra e fu suggerita per l'esplorazione dei parametri della bassa ionosfera sui corpi celesti. Possono anche essere usate per tracciare disturbi geomagnetici e ionosferici. Recentemente, le risonanze di Schumann vengono sfruttate per monitorare eventi luminosi transitori – sprite, getti, elfi, e altri fulmini dell'alta atmosfera. Un altro campo di interesse nell'uso della risonanza di Schumann è relativo alla previsione a breve termine di terremoti. La risonanza di Schumann è andata oltre ai limiti della fisica, invadendo la medicina, interessando artisti e musicisti, e guadagnando interesse in frange come la psicobiologia.

Teoria di base

Le scariche dei fulmini sono considerate la prima sorgente naturale delle risonanze di Schumann. I canali dei fulmini si comportano come un'enorme antenna che irradia energia elettromagnetica come segnali impulsivi a frequenze sotto i 100 kHz[17]. Questi segnali sono molto deboli, ma la guida d'onda Terra-ionosfera si comporta come un risonatore alle frequenze ELF e amplifica i segnali spettrali dei fulmini alle frequenze di risonanza[17].

In una cavità ideale, la frequenza di risonanza del modo ennesimo è determinata dal raggio terrestre e dalla velocità della luce [8].

La guida d'onda Terra-ionosfera reale non è una cavità elettromagnetica perfetta. Perdite dovute alla conduttività elettrica finita della ionosfera fanno risonare il sistema a frequenze più basse di quelle attese nel caso ideale, e i picchi osservati sono larghi. Inoltre ci sono una serie di asimmetrie orizzontali – transizione giorno-notte, cambiamenti latitudinali nel campo magnetico terrestre, disturbi improvvisi nella ionosfera, assorbimento nella calotta polare, ecc. che complicano lo spettro di potenza della risonanza di Schumann.

Misure

Oggi le risonanze di Schumann sono registrate da molte stazioni attorno al mondo. I sensori elettromagnetici usati per misurarle consistono in due antenne orizzontali per ricevere il campo magnetico nelle direzioni nord-sud ed est-ovest e un'antenna verticale per osservare il campo elettrico verticale. Siccome le frequenze di risonanza di Schumann sono estremamente basse, antenne pratiche dovrebbero misurare centinaia di chilometri. Inoltre, il campo elettrico di risonanza di Schumann è molto più piccolo del campo elettrico statico nell'atmosfera e il campo magnetico di risonanza di Schumann è inferiore di diversi ordini di grandezza rispetto a quello terrestre[18]. Quindi servono ricevitori speciali per misurare le risonanze di Schumann. La componente elettrica viene di solito misurata con un'antenna sferica, suggerita da Ogawa et al. nel 1966[19], collegata a un amplificatore ad alta impedenza. Il campo magnetico viene misurato con spire di induzione consistenti in decine di migliaia di avvolgimenti attorno a materiali con una altissima permeabilità magnetica.

Applicazioni

Attività globale dei fulmini

Inizialmente gli studi di Schumann sulla risonanza furono utilizzati per monitorare l'attività globale dei fulmini seguendo i cambiamenti nell'intensità dei campi di risonanza di Schumann. In un qualsiasi momento nel mondo ci sono circa 2 000 tempeste di fulmini[20]. Producendo circa 50 scariche al secondo[21], queste tempeste creano il segnale di risonanza di Schumann di fondo.

Determinare la distribuzione spaziale dei fulmini dalle registrazioni della risonanza di Schumann è un problema complesso: per poter stimare correttamente l'intensità dei fulmini da tali rilevazioni è necessario tener conto della distanza delle sorgenti dei fulmini. Il metodo comune è fare assunzioni preliminari sulla distribuzione spaziale dei fulmini, basandosi sulle proprietà conosciute della climatologia dei fulmini. Un metodo alternativo è mettere un ricevitore al polo nord o al polo sud, che rimarrebbe approssimativamente equidistante dai centri principali delle tempeste di fulmini durante il giorno[22].

Variazioni diurne

Le caratteristiche meglio documentate e dibattute del fenomeno della risonanza di Schumann sono le variazioni diurne dello spettro di potenza di fondo della risonanza di Schumann.

Una caratteristica che le registrazioni diurne della risonanza di Schumann riflettono sono le proprietà conosciute dell'attività globale dei fulmini. Il campo elettrico verticale, il quale è egualmente sensibile in tutte le direzioni e quindi misura i fulmini nel mondo, mostra tre massimi dominanti, associati con tre "hot spot" dell'attività planetaria dei fulmini: 9 picchi UT (Tempo universale), collegati alla incrementata attività elettrica del Sud-est asiatico; 14 picchi UT associati con il picco nell'attività dai fulmini in Africa; e i 20 picchi UT risultati nell'incremento dell'attività elettrica nel Sudamerica. Il tempo e l'ampiezza dei picchi varia durante l'anno, riflettendo i cambiamenti stagionali nell'attività elettrica.

Classifica dei "camini"

In generale il picco africano è il più forte, riflettendo il maggior contributo del "camino" africano all'attività globale dei fulmini. La posizione degli altri due picchi – asiatico e americano – è soggetta a vigorose dispute tra gli scienziati che studiano la risonanza di Schumann. Osservazioni condotte in Europa mostrano un contributo maggiore dall'Asia, rispetto al Sudamerica. Questo contraddice i dati climatologici e quelli ottenuti tramite satelliti ottici sui fulmini, che mostrano che il centro dei temporali sudamericano è più forte di quello asiatico[21]. La ragione di tale disparità non è chiara, ma potrebbe essere in relazione con la frequenza di 60 Hz dell'elettricità usata nel Nord America (60 Hz è una delle risonanze di Schumann). Williams e Sátori[23] suggeriscono che, per ottenere una classifica "corretta" dei camini asiatici e americani, è necessario rimuovere l'influenza data dalle variazioni giorno/notte sulla conduttività della ionosfera (l'influenza dell'asimmetria tra il giorno e la notte) dalle registrazioni della risonanza di Schumann.

D'altra parte, queste registrazioni "corrette" presentate nel lavoro di Sátori et al.[24] mostrano che anche dopo la rimozione dell'influenza dell'asimmetria tra il giorno e la notte dai tracciati della risonanza di Schumann, il contributo asiatico rimane maggiore di quello americano. Risultati simili sono stati ottenuti da Pechony et al.[25], che hanno calcolato i campi di risonanza di Schumann da dati sui fulmini presi dai satelliti. Si era assunto che la distribuzione dei fulmini nelle mappe satellitari fosse una buona rappresentazione delle fonti d'eccitazione, anche se le osservazioni satellitari misurano prevalentemente i fulmini fra nube e nube, piuttosto che quelli fra nubi e terra, che sono i principali eccitatori delle risonanze. Entrambe le simulazioni – quelle che trascuravano l'asimmetria giorno-notte e quelle che tenevano conto di tale asimmetria – mostravano i camini asiatici e americani nello stesso ordine. A oggi, il motivo delle posizioni "invertite" dei camini di Asia e America nei tracciati della risonanza di Schumann rimane poco chiaro, e l'argomento richiede un'ulteriore, più mirata ricerca.

Influenza della asimmetria tra giorno e notte

Nella letteratura iniziale le variazioni diurne osservate nella potenza della risonanza di Schumann furono spiegate con la variazione della geometria del sistema sorgente-ricevitore (fulmine-osservatore)[12]. Fu concluso che nessuna particolare variazione sistematica della ionosfera (che serve da limite superiore per la guida d'onda) era necessaria a spiegare queste variazioni[26]. Studi teorici successivi supportavano le prime stime della piccola influenza data dall'asimmetria giorno-notte della ionosfera (la differenza tra la conduttività diurna e notturna della ionosfera) sulle variazioni osservate nelle intensità dei campi di risonanza di Schumann[27].

L'interesse nell'influenza dell'asimmetria giorno-notte nella conduttività della ionosfera sulle risonanze di Schumann riprese forza negli anni novanta, dopo la pubblicazione di un lavoro di Sentman e Fraser[28]. Essi svilupparono una tecnica per separare i contributi globali e locali alle variazioni osservate nel campo di potenza utilizzando i tracciati ottenuti simultaneamente da due stazioni. Sentman e Fraser interpretarono i contributi locali come variazioni nell'altezza della ionosfera. Il loro lavoro convinse molti scienziati dell'importanza della asimmetria giorno-notte ionosferica e ispirarono numerosi studi sperimentali. Tuttavia recentemente è stato mostrato che i risultati ottenuti da Sentman e Fraser possono essere simulati con un modello uniforme (senza tenere conto della variazione giorno-notte nella ionosfera) e quindi non possono essere interpretati in termini di variazione di altezza nella ionosfera[29].

I tracciati dell'ampiezza della risonanza di Schumann mostrano variazioni diurne e stagionali significative, che in genere coincidono nel tempo con i tempi della transizione giorno-notte (il terminatore solare, la linea sulla quale la luce solare risulta tangente alla crosta terrestre). Questa corrispondenza temporale sembra supportare il suggerimento di una significativa influenza dell'asimmetria ionosferica sulle ampiezze della risonanza di Shumann. Ci sono tracciati che mostrano l'accuratezza di un orologio nei cambiamenti di ampiezza diurni[24]. D'altra parte ci sono molti giorni in cui le ampiezze della risonanza di Schumann non aumentano all'alba o non diminuiscono al tramonto. Ci sono studi che mostrano che il comportamento generico dei tracciati di ampiezza della risonanza di Schumann possono essere ricreati dalla migrazione diurna e stagionale delle tempeste di fulmini, senza invocare variazioni ionosferiche[25][27]. Due studi teorici indipendenti hanno mostrato che le variazioni nella potenza nella risonanza di Schumann relativi alla transizione giorno-notte sono molto più piccoli di quelli associati ai picchi nell'attività globale dei fulmini, e che quindi tale attività globale gioca un ruolo molto più importante nella variazione nella potenza di tale risonanza[25][30].

L'importanza relativa dell'asimmetria giorno-notte nei tracciati dell'ampiezza della risonanza di Schumann è ancora discussa. Il successo nel monitoraggio dell'attività elettrica globale con le risonanze di Schumann si affida alla corretta interpretazione dei dati sperimentali. È quindi vitale capire e interpretare correttamente le caratteristiche maggiori delle variazioni nella potenza del campo della risonanza di Schumann.

Il "problema inverso"

Uno dei problemi interessanti negli studi sulla risonanza di Schumann è la determinazione delle caratteristiche delle sorgenti di fulmini (il "problema inverso"). Trovare temporalmente ogni singola scarica è impossibile, ma ci sono intensi eventi transitori nelle ELF, anche chiamati ‘‘Q burst'’. I Q-burst sono azionati da scariche elettriche intense, associate a un grande trasferimento di carica e spesso a un'alta corrente di picco[19]. I Q-burst possono superare l'ampiezza del segnale di fondo di un fattore di 10 e appaiono a intervalli di circa 10 secondi[31], il che permette di considerarli eventi isolati e di determinare il luogo del fulmine che li ha generati. La posizione della sorgente viene determinata con tecniche sia multi-stazione sia a stazione singola. Quelle multistazione sono più accurate, ma richiedono laboratori più complessi e costosi.

Ricerca sugli eventi luminosi transitori

Si crede ora che molti dei transitori nella risonanza di Schumann (Q burst) sono legati a eventi luminosi transitori (TLE). Nel 1995 Bocippio et al.[32] suggerì che gli sprite, i più comuni TLE, sono prodotti da fulmini positivi nuvola-terra che avvengono nella regione stratiforme di un sistema di tempesta, e vengono accompagnati da Q burst nelle bande di risonanza di Schumann. Osservazioni recenti[32][33] rivelano che le occorrenze di sprite e Q burst sono molto correlate e i dati sulla risonanza di Schumann possono essere usati per stimare la quantità di sprite che avvengono globalmente[34].

Ricerche sui cambiamenti climatici

Il mutamento climatico globale è soggetto da intensi dibattiti e preoccupazioni. Uno degli aspetti importanti nel capire tale mutamento è lo sviluppo di strumenti e tecniche che permetteranno un monitoraggio continuo e a lungo termine dei processi che interessano il clima globale. Le risonanze di Schumann sono uno dei pochissimi strumenti che possono fornire tali informazioni globali prontamente ed economicamente.

Temperatura globale

Williams [1992][35] ha suggerito che la temperatura globale potrebbe essere monitorata con le risonanze di Schumann. Il collegamento tra la risonanza di Schumann e la temperatura è la frequenza di scariche elettriche, che aumenta non linearmente con la temperatura[35]. La non linearità della relazione tra fulmini e temperatura fornisce un amplificatore naturale dei cambiamenti della temperatura e rende la risonanza di Schumann un "termometro" sensibile. Inoltre, le particelle di ghiaccio che si crede partecipino nei processi di elettrificazione che risultano in una scarica elettrica[36] hanno un ruolo importante nelle risposte degli effetti radioattivi che influenzano la temperatura atmosferica. Le risonanze di Schumann potrebbero quindi aiutarci a capire questi effetti di retroazione.

Vapore acqueo nella troposfera superiore

Il vapore acqueo troposferico è un elemento chiave nel clima terrestre, che ha effetti diretti come un gas serra, così come un effetto indiretto attraverso l'interazione con le nuvole, gli aerosol e la chimica troposferica. Il vapore acqueo nella troposfera superiore (Upper Troposferic Water Vapor, UTWV) ha un impatto molto più grande sull'effetto serra rispetto al vapore acqueo nella bassa atmosfera[37], ma se questo impatto sia una retroazione positiva o negativa è ancora incerto[38]. La sfida principale nel rispondere a questa domanda è la difficoltà nel monitorare il vapore acqueo nella troposfera superiore globalmente in lunghi periodi di tempo. Le tempeste di fulmini date da nuvole convettive profonde producono la maggior parte di scariche elettriche sulla Terra. In aggiunta, esse trasportano una grande quantità di vapore acqueo nell'alta troposfera, dominando di fatto le variazioni nella quantità globale di vapore acqueo nella troposfera superiore. Price [2000][39] ha suggerito che i cambiamenti nel vapore acqueo nella troposfera superiore possono essere derivati dai tracciati delle risonanze di Schumann.

Fulmini extraterrestri

L'esistenza delle risonanze di Schumann è condizionata primariamente da due fattori:

  1. la presenza di una sostanziale ionosfera con la conduttività elettrica che aumenta con l'altitudine da valori bassi vicino alla superficie (o uno strato ad alta conduttività, nel caso di pianeti gassosi);
  2. la sorgente dell'eccitazione delle onde elettromagnetiche nella gamma ELF. Nel sistema solare ci sono cinque candidati per la rilevazione della risonanza di Schumann: Venere, Marte, Giove, Saturno e la sua luna Titano.

Modellare le risonanze di Schumann sui pianeti e sulle lune del sistema solare è complicato dalla mancanza di conoscenza dei parametri della guida d'onda, e a oggi non vi è la possibilità di validare i risultati. Tuttavia i risultati teorici aiutano a stimare la possibilità di rilevare le risonanze di Schumann su di un pianeta.

La prova più forte per i fulmini su Venere viene dalle onde elettromagnetiche impulsive rilevate dai lander Venera 11 e 12. Le risonanze di Schumann su Venere sono state studiate da Nickolaenko e Rabinowicz [1982][40] e da Pechony e Price [2004][41]. Entrambi gli studi diedero risultati molto vicini, indicando che le risonanze di Schumann dovrebbero essere facilmente rilevabili su questo pianeta, sempre che un qualsiasi sensore sopravviva abbastanza a lungo nel duro ambiente venusiano.

Su Marte non è stata rilevata alcuna attività elettrica, ma la separazione delle cariche e i fulmini sono considerati possibili nelle tempeste di polvere marziane[42][43]. Le risonanze globali marziane sono state modellate da Sukhorukov [1991][44], da Pechony e Price [2004][41] e da Molina Cuberos ed al. [2006][45]. I risultati dei tre studi sono in qualche modo differenti, ma sembra che almeno i primi due modi di risonanza di Schumann dovrebbero essere rilevabili.

È stato a lungo suggerito che scariche elettriche avvengano su Titano[46], ma i recenti dati inviati dalla sonda Cassini-Huygens sembrano indicare che non c'è attività di fulmini sul più grande satellite di Saturno. A causa del recente interesse verso Titano, associato alla missione Cassini-Huygens, la sua ionosfera è forse la più completamente modellata oggi. Le risonanze di Schumann su Titano sono state studiate da Besser et al. [2002][47], da Morente et al. [2003][48], Molina-Cuberos et al. [2004][49], Nickolaenko et al. [2003][50] e da Pechony e Price [2004][41]. Sembra che solo il primo modo della risonanza di Schumann potrebbe essere rilevato su Titano.

Giove è l'unico pianeta dove l'attività dei fulmini è ben stabilita. L'esistenza dell'attività elettrica su questo pianeta è stata prevista da Bar-Nun [1975][51] ed è ora supportata dai dati della sonda Galileo, Voyager 1 e Voyager 2, Pioneer 10 e 11 e della Cassini-Huygens. Anche su Saturno ci si aspetta di trovare una intensa attività elettrica, ma le tre sonde che lo hanno visitato – la Pioneer 11 nel 1979, la Voyager 1 nel 1980 e la Voyager 2 nel 1982, non hanno fornito finora alcuna prova convincente. Anche la forte tempesta monitorata su Saturno dalla sonda Cassini non ha prodotto fulmini visibili. Poco si sa dei parametri elettrici dell'interno di Giove e Saturno. Anche la domanda su quale sarebbe il limite inferiore della guida d'onda è un problema non banale per i pianeti gassosi. Sembra che non ci siano lavori dedicati alla risonanza di Schumann su Saturno. C'è stato solo un singolo tentativo di modellare le risonanze di Schumann su Giove[52]. Se qualcuno trovasse il modo di appendere un sensore per la risonanza di Schumann nell'atmosfera di Giove, allora le risonanze di Schumann potrebbero essere facilmente rilevate.

Cultura di massa

Note

  1. ^ O. Heaviside, Telegraphy, Sect. 1, Theory., in Encyc. Brit.10th ed. London, vol. 9, 1902, pp. 213-218.
  2. ^ A.E. Kennelly, On the elevation of the electrically-conducting strata of the earth's atmosphere, in Electrical world and engineer, vol. 32, 1902, pp. 473-473.
  3. ^ Appleton, E. V., M. A. F. Barnett, On Some Direct Evidence for Downward Atmospheric Reflection of Electric Rays, in Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 109(752), 1925, pp. 621-641.
  4. ^ «In pratica un grande condensatore che Tesla riuscì a far vibrare con l'energia elettrica.» Cfr. Vittorio Baccelli, Nikola Tesla - un genio volutamente dimenticato, Edizioni della Mirandola, maggio 2007, p. 55.
  5. ^ Nickolaenko, Alexander, and Masashi Hayakawa: "Schumann Resonance for Tyros", Springer, 2014.
  6. ^ N. Tesla, The Transmission of Electrical Energy Without Wires As A Means Of Furthering World Peace, in Electrical World And Engineer, January 7, 1905, pp. 21-24.
  7. ^ Watson, G.N., The diffraction of electric waves by the Earth, in Proc. Roy. Soc. (London), Ser.A 95, 1918, pp. 83-99.
  8. ^ a b Schumann W. O., Über die strahlungslosen Eigenschwingungen einer leitenden Kugel, die von einer Luftschicht und einer Ionosphärenhülle umgeben ist, in Zeitschrift und Naturfirschung, 7a, 1952, pp. 149-154.
  9. ^ Schumann W. O., Über die Dämpfung der elektromagnetischen Eigenschwingnugen des Systems Erde – Luft – Ionosphäre, in Zeitschrift und Naturfirschung, 7a, 1952, pp. 250-252.
  10. ^ Schumann W. O., Über die Ausbreitung sehr Langer elektriseher Wellen um die Signale des Blitzes, in Nuovo Cimento, vol. 9, 1952, pp. 1116-1138.
  11. ^ Schumann W. O. and H. König, Über die Beobactung von Atmospherics bei geringsten Frequenzen, in Naturwiss, vol. 41, 1954, pp. 183-184.
  12. ^ a b Balser M. and C. Wagner, Measurement of the spectrum of radio noise from 50 to 100 c/s, in J.Res. NBS, 64D, 1960, pp. 415-418.
  13. ^ Balser M. and C. Wagner, Observations of earth-ionosphere cavity resonances, in Nature, vol. 188, 1960, pp. 638-641.
  14. ^ Balser M. and C. Wagner, Diurnal power variations of the earth-ionosphere cavity modes and their relationship to worldwide thunderstorm activity, in J.G.R, vol. 67, 1962, pp. 619-625.
  15. ^ Balser M. and C. Wagner, On frequency variations of the earth-ionosphere cavity modes, in J.G.R, vol. 67, 1962, pp. 4081-4083.
  16. ^ Balser M. and C. Wagner, Effect of a high-altitude nuclear detonation on the earth-ionosphere cavity, in J.G.R, vol. 68, 1963, pp. 4115-4118.
  17. ^ a b Volland, H., Atmospheric Electrodynamics, Springer-Verlag, Berlin, 1984.
  18. ^ Price, C., O. Pechony, E. Greenberg, Schumann resonances in lightning research, in Journal of Lightning Research, vol. 1, 2006, pp. 1-15.
  19. ^ a b Ogawa, T., Y. Tanka, T. Miura, and M. Yasuhara, Observations of natural ELF electromagnetic noises by using the ball antennas, in J. Geomagn. Geoelectr, vol. 18, 1966, pp. 443-454.
  20. ^ Heckman S. J., E. Williams,, Total global lightning inferred from Schumann resonance measurements, in J. G. R., 103(D24), 1998, pp. 31775-31779.
  21. ^ a b Christian H. J., R.J. Blakeslee, D.J. Boccippio, W.L. Boeck, D.E. Buechler, K.T. Driscoll, S.J. Goodman, J.M. Hall, W.J. Koshak, D.M. Mach, M.F. Stewart,, Global frequency and distribution of lightning as observed from space by the Optical Transient Detector, in J. G. R., 108(D1), 2003, p. 4005.
  22. ^ Nickolaenko, A.P., Modern aspects of Schumann resonance studies, in J.A.S.T.P., vol. 59, 1997, pp. 806-816.
  23. ^ Williams E. R., G. Sátori, Lightning, thermodynamic and hydrological comparison of the two tropical continental chimneys, in J.A.S.T.P., vol. 66, 2004, pp. 1213-1231.
  24. ^ a b Sátori G., M. Neska, E. Williams, J. Szendro"i, Signatures of the non-uniform Earth-ionosphere cavity in high time-resolution Schumann resonance records, in Radio Science, in print, 2007.
  25. ^ a b c Pechony, O., C. Price, A.P. Nickolaenko, Relative importance of the day-night asymmetry in Schumann resonance amplitude records, in Radio Science, in print, 2007.
  26. ^ Madden T., W. Thompson, Low-frequency electromagnetic oscillations of the Earth-ionosphere cavity, in Rev. Geophys., 3(2), 1965, p. 211.
  27. ^ a b title Resonances in the Earth-ionosphere cavity Nickolaenko A. P. and M. Hayakawa, Kluwer Academic Publishers, Dordrecht-Boston-London, 2002.
  28. ^ Sentman, D.D., B. J. Fraser, Simultaneous observations of Schumann Resonances in California and Australia - Evidence for intensity modulation by the local height of the D region, in Journal of geophysical research, 96(9), 1991.
  29. ^ Pechony, O., C. Price, Schumann Resonances: interpretation of local diurnal intensity modulations, in Radio Sci., 41, 42(2), 2006.
  30. ^ Yang H., V. P. Pasko, Three-dimensional finite difference time domain modeling of the diurnal and seasonal variations in Schumann resonance parameters, in Radio Science, vol. 41, 2007.
  31. ^ Shvets A.V., A technique for reconstruction of global lightning distance profile from background Schumann resonance signal, in J.A.S.T.P., vol. 63, 2001, pp. 1061-1074.
  32. ^ a b Boccippio, D. J., E. R. Williams, S. J. Heckman, W. A. Lyons, I. T. Baker, R. Boldi, Sprites, ELF transients, and positive ground strokes, in Science, vol. 269, 1995, pp. 1088-1091.
  33. ^ Price, C., E. Greenberg, Y. Yair, G. Sátori, J. Bór, H. Fukunishi, M. Sato, P. Israelevich, M. Moalem, A. Devir, Z. Levin, J.H. Joseph, I. Mayo, B. Ziv, A. Sternlieb, Ground-based detection of TLE-producing intense lightning during the MEIDEX mission on board the Space Shuttle Columbia, in G.R.L., vol. 31, 2004.
  34. ^ Hu, W., S. A. Cummer, W. A. Lyons, T. E. Nelson, Lightning charge moment changes for the initiation of sprites, in G.R.L., 29(8), 2002, p. 1279.
  35. ^ a b Williams, E.R., The Schumann resonance: a global tropical thermometer, in Science, vol. 256, 1992, pp. 1184-1186.
  36. ^ Williams, E.R., The tripole structure of thunderstorms, in J. G. R., vol. 94, 1989, pp. 13151-13167.
  37. ^ Hansen, J., A. Lacis, D. Rind, G. Russel, P. Stone, I. Fung, R. Ruedy, J., Lerner, Climate sensitivity: Analysis of feedback mechanisms, in Climate Processes and Climate Sensitivity, J.,E. Hansen and T. Takahashi, eds.. AGU Geophys. Monograph, vol. 29, 1984, pp. 130-163.
  38. ^ Rind, D., Just add water vapor, in Science, vol. 28, 1998, pp. 1152-1153.
  39. ^ Price, C., Evidence for a link between global lightning activity and upper tropospheric water vapor, in Letters to Nature, vol. 406, 2000, pp. 290-293.
  40. ^ Nickolaenko A. P., L. M. Rabinowicz, On the possibility of existence of global electromagnetic resonances on the planets of Solar system, in Space Res., vol. 20, 1982, pp. 82-89.
  41. ^ a b c Pechony, O., C. Price, Schumann resonance parameters calculated with a partially uniform knee model on Earth, Venus, Mars, and Titan, in Radio Sci., 39(5), 2004.
  42. ^ Eden, H. F. and B. Vonnegut, Electrical breakdown caused by dust motion in low-pressure atmospheres: consideration for Mars, in Science, vol. 180, 1973, p. 962.
  43. ^ Renno N. O., A. Wong, S. K. Atreya, I. de Pater, M. Roos-Serote, Electrical discharges and broadband radio emission by Matian dust devils and dust storms, in G. R. L., 30 (22), 2003, p. 2140.
  44. ^ Sukhorukov A. I., On the Schumann resonances on Mars, in Planet. Space Sci., 39(12), 1991, pp. 1673-1676.
  45. ^ Molina-Cuberos G. J., J. A. Morente, B. P. Besser, J. Porti, H. Lichtenegger, K. Schwingenschuh, A. Salinas, J. Margineda, Schumann resonances as a tool to study the lower ionosphere of Mars, in Radio Science, vol. 41, 2006.
  46. ^ Lammer H., T. Tokano, G. Fischer, W. Stumptner, G. J. Molina-Cuberos, K. Schwingenschuh, H. O. Rucher, Lightning activity of Titan: can Cassiny/Huygens detect it?, in Planet. Space Sci., vol. 49, 2001, pp. 561-574.
  47. ^ Besser, B. P., K. Schwingenschuh, I. Jernej, H. U. Eichelberger, H. I. M. Lichtenegger, M. Fulchignoni, G. J. Molina-Cuberos, J. A. Morente, J. A. Porti, A.Salinas, Schumann resonances as indicators for lighting on Titan, in Proceedings of the Second European Workshop on Exo/Astrobiology, Graz, Australia, 16-19 Sep., 2002.
  48. ^ Morente J. A., Molina-Cuberos G. J., Porti J. A., K. Schwingenschuh, B. P. Besser, A study of the propagation of electromagnetic waves in Titan’s atmosphere with the TLM numerical method, in Icarus, vol. 162, 2003, pp. 374-384.
  49. ^ Molina-Cuberos G. J., J. Porti, B. P. Besser, J. A. Morente, J. Margineda, H. I. M. Lichtenegger, A. Salinas, K. Schwingenschuh, H. U. Eichelberger, Schumann resonances and electromagnetic transparence in the atmosphere of Titan, in Advances in Space Research, vol. 33, 2004, pp. 2309-2313.
  50. ^ Nickolaenko A. P., B. P. Besser, K. Schwingenschuh, Model computations of Schumann resonance on Titan, in Planet. Space Sci., 51(13), 2003, pp. 853-862.
  51. ^ Bar-Nun A., Thunderstorms on Jupiter, in ICARUS, vol. 24, 1975, pp. 86-94.
  52. ^ Sentman D. D., Electrical conductivity of Jupiter's Shallow interior and the formation of a resonant planetary-ionosphere cavity, in ICARUS, vol. 88, 1990, pp. 73-86.

Bibliografia

  • Nickolaenko, Alexander, and Masashi Hayakawa. "Schumann Resonance for Tyros.", Springer, 2014.

Voci correlate

Altri progetti

Collegamenti esterni

Riferimenti generici

Siti web

  Portale Elettromagnetismo