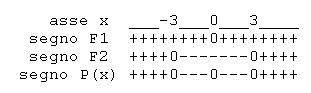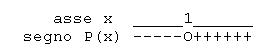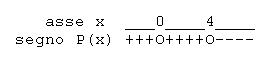Una disequazione si dice disequazione intera se, messa in forma normale, si presenta nella forma
 oppure
oppure  oppure
oppure  oppure
oppure 
dove  è un polinomio nella lettera x. In base al grado del polinomio la disequazione intera sarà di primo, secondo, terzo grado,...
è un polinomio nella lettera x. In base al grado del polinomio la disequazione intera sarà di primo, secondo, terzo grado,...
Esempi
 è una disequazione intera di primo grado.
è una disequazione intera di primo grado. è una disequazione intera di secondo grado.
è una disequazione intera di secondo grado. è una disequazione intera di terzo grado, ma non in forma normale.
è una disequazione intera di terzo grado, ma non in forma normale. è una disequazione fratta, in quanto l'incognita è presente anche a denominatore.
è una disequazione fratta, in quanto l'incognita è presente anche a denominatore.
Risoluzione disequazioni intere di primo grado
Fare riferimento alla voce Disequazione.
Risoluzione disequazioni intere di secondo grado
Fare riferimento alla voce disequazione di 2° grado.
Risoluzione disequazioni intere di grado superiore al secondo
Vi sono due metodi risolutivi.
Metodo della scomposizione in fattori e dello studio del segno del prodotto
La procedura prevede:
- mettere in forma normale la disequazione;
- fattorizzare il polinomio
 a primo membro in fattori di 1° e/o di 2º grado;
a primo membro in fattori di 1° e/o di 2º grado;
- studiare il segno di ciascun fattore (sempre per
 o per
o per  in relazione alla presenza dell'uguale nella disequazione);
in relazione alla presenza dell'uguale nella disequazione);
- rappresentare graficamente il segno di tutti i fattori e comporre il segno del prodotto;
- evidenziare quei valori per cui i fattori si annullano con un simbolo particolare (ad esempio O);
- guardando il verso della disequazione in forma normale, individuare sul grafico del segno di
 l'insieme delle soluzioni, cioè l'intervallo dell'asse reale che soddisfa la disequazione.
l'insieme delle soluzioni, cioè l'intervallo dell'asse reale che soddisfa la disequazione.
Esempio 1

La disequazione non è in forma normale quindi

Fattorizzazione di  .
.

Studio del segno dei fattori (sempre per  ):
):
 ;
; è una disequazione di 2° grado;
è una disequazione di 2° grado; sempre positiva in
sempre positiva in  .
.
Schema del segno di 
Soluzioni.
Si chiede che  sia negativo o nullo (guardare il verso della disequazione in forma normale). Le soluzioni della disequazione sono
sia negativo o nullo (guardare il verso della disequazione in forma normale). Le soluzioni della disequazione sono  .
.
Esempio 2

La disequazione non è in forma normale quindi

Fattorizzazione di  .
.
 .
.
Studio del segno dei fattori (sempre per  ).
).
 un quadrato è sempre positivo, nullo per x=0, mai negativo.
un quadrato è sempre positivo, nullo per x=0, mai negativo. è una disequazione di 2° grado.
è una disequazione di 2° grado. (EA)
(EA)  positiva per
positiva per  .
.
Schema del segno di 
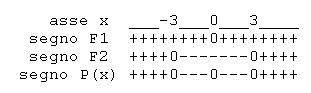
Soluzioni.
Si chiede che  sia positivo o nullo (guardare il verso della disequazione in forma normale). Le soluzioni della disequazione sono
sia positivo o nullo (guardare il verso della disequazione in forma normale). Le soluzioni della disequazione sono  .
.
Metodo veloce del segno di P(x)
La procedura risolutiva prevede:
- mettere in forma normale la disequazione;
- risolvere l'equazione associata (EA)
 e trovare le soluzioni della EA con la loro molteplicità;
e trovare le soluzioni della EA con la loro molteplicità;
- rappresentare graficamente il segno di
 partendo sempre da destra con il segno del coefficiente della
partendo sempre da destra con il segno del coefficiente della  di grado massimo;
di grado massimo;
- nello schema grafico cambiare il segno solo quando si incontra una radice (soluzione) di EA con molteplicità dispari;
- guardando il verso della disequazione in forma normale, individuare sul grafico del segno di
 l'insieme delle soluzioni, cioè l'intervallo dell'asse reale che soddisfa la disequazione.
l'insieme delle soluzioni, cioè l'intervallo dell'asse reale che soddisfa la disequazione.
Esempio 3

La disequazione non è in forma normale quindi:

Equazione associata (EA) 

Si tratta di una equazione binomia con un'unica soluzione  con molteplicità 1. Il coefficiente della
con molteplicità 1. Il coefficiente della  di grado massimo vale 1 (positivo) dunque:
di grado massimo vale 1 (positivo) dunque:
schema del segno di 
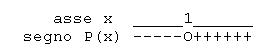
Soluzioni.
Si chiede che  sia negativo o nullo (guardare il verso della disequazione in forma normale). Le soluzioni della disequazione sono
sia negativo o nullo (guardare il verso della disequazione in forma normale). Le soluzioni della disequazione sono  .
.
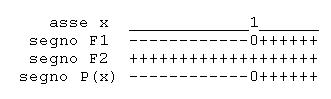
Esempio 4

La disequazione è in forma normale.
Equazione associata (EA)

Si tratta di una equazione generica che va risolta mediante scomposizione

Le cui soluzioni sono  con molteplcità 6 e
con molteplcità 6 e  con molteplcità 1. Il coefficiente della
con molteplcità 1. Il coefficiente della  di grado massimo vale -2 (negativo) dunque:
di grado massimo vale -2 (negativo) dunque:
schema del segno di 
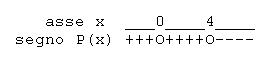
Attenzione: in  il segno non cambia perché ha molteplicità 6 (pari).
il segno non cambia perché ha molteplicità 6 (pari).
Soluzioni.
Si chiede che  sia negativo o nullo (guardare il verso della disequazione in forma normale). Le soluzioni della disequazione sono
sia negativo o nullo (guardare il verso della disequazione in forma normale). Le soluzioni della disequazione sono  .
.
Esempio 5

La disequazione è in forma normale.
Equazione associata (EA)

Si tratta di una equazione generica che va risolta mediante scomposizione

Le cui soluzioni sono  con molteplcità 2 e
con molteplcità 2 e  e
e  con molteplcità 1. Il coefficiente della
con molteplcità 1. Il coefficiente della  di grado massimo vale 1 (positivo) dunque:
di grado massimo vale 1 (positivo) dunque:
schema del segno di 

Attenzione: in  il segno non cambia perché ha molteplicità 2 (pari).
il segno non cambia perché ha molteplicità 2 (pari).
Soluzioni.
Si chiede che  sia positivo o nullo (guardare il verso della disequazione in forma normale). Le soluzioni della disequazione sono
sia positivo o nullo (guardare il verso della disequazione in forma normale). Le soluzioni della disequazione sono  .
.
Casi particolari
Potenze con esponente pari

Questa disequazione presenta a primo membro una potenza con esponente pari. Una potenza con esponente pari è sempre positiva o nulla, mai negativa. Quindi, anche se la disequazione non è in forma normale, sappiamo che non sarà mai verificata.

Potenze con esponente dispari

Questa disequazione presenta al primo membro una potenza con esponente dispari. Una potenza con esponente dispari segue il segno della base. Quindi, anche se la disequazione non è in forma normale, sappiamo sarà verificata quando

Disequazioni intere con polinomio già fattorizzato

Questa disequazione presenta a primo membro già un polinomio fattorizzato. In questo caso conviene usare il metodo del segno dei fattori
 è una potenza con esponente pari, dunque positiva sempre eccetto in
è una potenza con esponente pari, dunque positiva sempre eccetto in  dove vale 0;
dove vale 0; è una potenza con esponente dispari, dunque segue il segno della base
è una potenza con esponente dispari, dunque segue il segno della base  ;
; è una potenza con esponente pari, dunque sempre positiva o nulla per
è una potenza con esponente pari, dunque sempre positiva o nulla per  .
.
Schema del segno
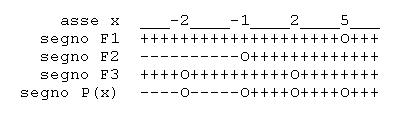
Soluzioni.
 deve essere negativo, quindi per
deve essere negativo, quindi per  .
.
Disequazioni di quarto grado riconducibili al secondo
Un caso particolare di disequazione di quarto grado è il seguente:
 (oppure
(oppure  ).
).
Questo tipo di disequazioni si risolve effettuando una divisione membro a membro per  , ossia:
, ossia:

e quindi, semplificando e raccogliendo i fattori comuni si ottiene:

poi si prosegue ponendo  e
e  come segue:
come segue:
 , da cui (elevando al quadrato entrambi i membri) si ottiene:
, da cui (elevando al quadrato entrambi i membri) si ottiene:
Sostituendo  e
e  nella disequazione precedente si ha una comune disequazione di secondo grado:
nella disequazione precedente si ha una comune disequazione di secondo grado:

Dopo aver risolto la disequazione di secondo grado operiamo la sostituzione inversa di  (è molto importante fare attenzione al dominio di risoluzione della disequazione di secondo grado).
(è molto importante fare attenzione al dominio di risoluzione della disequazione di secondo grado).
Se nella disequazione ottenuta non compare il termine di secondo grado:

allora si raccolgono i fattori comuni e si ottiene:

Bibliografia
- (IT) Dodero, Baroncini, Manfredi (1999): Lineamenti di Matematica 2 per il biennio delle scuole superiori, 2th edition, Ghisetti e Corvi Editori
Voci correlate
Collegamenti esterni