|
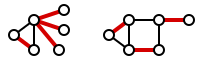
Copertura degli spigoliNella teoria dei grafi, una copertura degli spigoli di un grafo è un insieme di spigoli tale che ogni vertice del grafo è incidente ad almeno uno spigolo dell'insieme. Nell'informatica, il problema della copertura minima degli spigoli è il problema di trovare una copertura degli spigoli di dimensione minima. È un problema di ottimizzazione che appartiene alla classe dei problemi di copertura e può essere risolto in tempo polinomiale. DefinizioneFormalmente, la copertura degli spigoli di un grafo G è un insieme di spigoli C tale che ogni vertice in G è incidente con almeno uno spigolo in C. Si dice che l'insieme C copre i vertici di G. La figura seguente mostra esempi di coperture degli spigoli in due grafi. Una copertura minima degli spigoli è una copertura degli spigoli della dimensione più piccola possibile. Il numero delle coperture degli spigoli è la dimensione della copertura minima degli spigoli. La figura seguente mostra esempi di coperture minime degli spigoli. Si noti che la figura a destra non è soltanto una copertura sugli spigoli, ma anche un accoppiamento. In particolare, esso è un accoppiamento perfetto: un accoppiamento M in cui ciascun vertice è incidente con esattamente un vertice in M. Un accoppiamento perfetto è sempre una copertura minima degli spigoli. Esempi
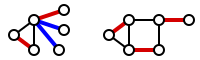
AlgoritmiUna copertura degli spigoli piccolissima può essere trovata nel tempo polinomiale trovando un accoppiamento massimo ed estendendolo "golosamente" (cioè mediante un "algoritmo goloso") così che tutti i vertici siano coperti.[1][2] Nella figura seguente, un accoppiamento massimo è segnato in rosso; gli spigoli supplementari che sono stati aggiunti per coprire i nodi non accoppiati sono segnati in blu. (La figura a destra mostra un grafo in cui un accoppiamento massimo è un accoppiamento perfetto; quindi copre già tutti i vertici e non sono stati necessari spigoli supplementari.) D'altro canto, il problema collegato di trovare una copertura dei vertici piccolissima è un problema NP-difficile.[1] Note
Bibliografia
Voci correlate
Collegamenti esterni
|