|
Théorie de la viabilitéLa théorie de la viabilité, proposée par Jean Pierre Aubin[1],[2] dans les années 1990, fournit un cadre formel pour étudier la compatibilité entre un système en évolution et des contraintes dans l'espace où le système évolue. 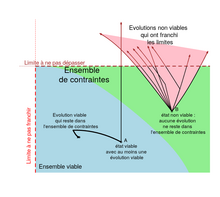 L'intérêt de cette théorie est de caractériser la propriété intrinsèque d'un système en évolution à pouvoir satisfaire des contraintes au cours du temps : une évolution est viable si elle reste dans l'ensemble de contraintes ; un état est viable s'il existe au moins une évolution viable à partir de cet état ; un ensemble est viable si tous ses états sont viables. Le plus grand des ensembles viables est appelé noyau de viabilité. Appliquée à des modèles dynamiques de problèmes réels, elle permet de déterminer la cohérence entre les contraintes qu'on souhaite respecter et les moyens (contrôles, régulations) qu'on se donne pour y parvenir. Les algorithmes associés à la théorie de la viabilité identifient l’ensemble des conditions (combinaison d’états et de contrôles) qui permettent au système de rester viable. Il est possible d'exploiter ces résultats pour proposer des stratégies d'actions viables, qui permettent de gouverner le système dynamique suivant des trajectoires satisfaisantes car elles resteront toujours dans l'ensemble de contraintes. Quand le noyau de viabilité est vide, aucun état n'est viable. Cela signifie que la dynamique (qui prend en compte les moyens d'actions et les incertitudes), et les contraintes qu'on souhaite respecter ne sont pas compatibles : il faut être moins exigeant sur les contraintes, ou réduire les incertitudes, ou se donner davantage de moyens d'actions. La théorie mathématique de la viabilité marque une rupture avec les approches des mathématiques de la décision basées sur la maximisation d'une utilité ou les approches « statiques » de la théorie de la décision. En effet, le choix des critères d'optimisation ou de la fonction objectif sont nécessairement subjectifs. L'approche de la viabilité permet de garantir le respect des contraintes en tout temps quels que soient les critères retenus par la suite pour calculer ou optimiser les trajectoires. Il n'est pas nécessaire, pour une analyse de viabilité, de choisir entre le court terme et le long terme, ni entre différents critères. Cette théorie est féconde pour formaliser les concepts liés à la durabilité : robustesse (comme capacité de rester dans l'ensemble de contraintes malgré des perturbations), résilience (comme capacité à retourner dans l'ensemble de contraintes malgré des perturbations)[3],[4], transition (comme capacité à atteindre une cible en restant dans un ensemble de contraintes), développement durable[5]. La théorie de la viabilité trouve de nombreuses applications dans les domaines liés à l'environnement, sans s'y limiter[2]. La théorie est utilisée pour la modélisation des problèmes de gestion des ressources renouvelables[6],[7]. Les exemples de modélisations abondent dans des domaines divers : élevage, pêcherie, forêts, eau, climat[8], agro-écologie, agroalimentaire etc. Certaines applications ont débouché sur des expérimentations dans le monde réel, en particulier pour le pilotage d'un petit sous-marin et pour fabriquer du camembert. Le noyau de viabilitéL'un des concepts majeurs de la théorie est le noyau de viabilité. Ce sous-ensemble de l'ensemble des contraintes rassemble tous les états viables pour la dynamique considérée. DéfinitionSoit un système dynamique et un ensemble de contraintes dans l'espace d'état. Le noyau de viabilité de relativement à est l'ensemble des états de à partir desquels il existe au moins une évolution gouvernée par qui reste dans indéfiniment. CorollaireA partir d'un état de l'ensemble des contraintes qui se trouve hors du noyau de viabilité, toutes les évolutions quittent l'ensemble de contraintes en temps fini. Si on souhaite que le système reste indéfiniment dans l'ensemble de contraintes dans le futur, il faut trouver un moyen de lui faire rejoindre le noyau de viabilité en temps fini. Exemple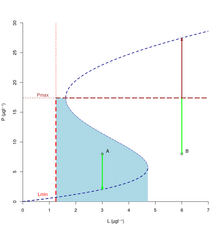 Paramètres : b=1,95 an-1 ; q=1,9 ; m=19,44 µg l-1 ; r=72,22 µg l-1 an-1; Lmin=1,25 µg l-1 ; Pmax=17,39 µg l-1 Notes : i) dans cet exemple, une trajectoire unique est issue de chaque état ii) ce noyau de viabilité est un noyau d'invariance (à l'intérieur du noyau, toutes les trajectoires gouvernées par la dynamique sont viables) La figure 1 ci-contre montre un exemple de noyau de viabilité pour un problème d'eutrophisation : l'accumulation de nutriments (comme le phosphore ou l'azote) dans l'eau d'un lac peut amener un changement d'état qui s'accompagne de prolifération d'algues, de dégradation de la qualité de l'eau et de la biodiversité, éventuellement de bloom bactérien. L'étude de la viabilité dans ce cas consiste à déterminer s'il est possible de concilier la pratique d'une activité qui apporte des nutriments et la conservation du lac dans un état souhaitable oligotrophe. Ici on souhaite que les apports soient supérieurs à un seuil (zone à droite de la verticale en pointillé rouge), pour tenir compte des besoins de l'activité agricole ; Et que la concentration du phosphore total soit inférieure à un seuil (zone sous la droite horizontale en pointillé marron) pour conserver le lac oligotrophe. Ces états souhaitables constituent l'ensemble de contraintes . On modélise l'évolution au cours du temps de la concentration du phosphore total dans le lac , en fonction des apports de phosphore , par une pseudo-sigmoïde [9] : 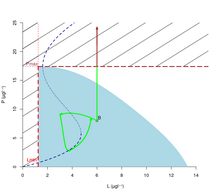 même paramètres que pour la figure 1, borne du contrôle Quand les apports de phosphore sont constants, suivant l'état de départ, l'état du lac évolue vers un équilibre eutrophe (la ligne haute de la courbe des équilibres) ou vers un équilibre oligotrophe (la ligne basse de la courbe des équilibres). La zone bleue de la Figure 1 rassemble les états qui évoluent naturellement vers les équilibres oligotrophes : c'est le noyau de viabilité de K pour la dynamique (1) avec constant. Le point B n'est pas dans le noyau de viabilité, le lac dans l'état B va évoluer hors de l'ensemble de contraintes et rejoindre un équilibre eutrophe.
Le point B de la figure 1, qui n'était pas viable en l'absence de contrôle, est maintenant dans le noyau de viabilité pour la dynamique contrôlée (1)(2). Le bassin de captureLa théorie de la viabilité s'intéresse aussi à la capacité d'un système dynamique de capturer une cible en temps fini (c'est-à-dire que les évolutions atteignent la cible) : c'est le bassin de capture. DéfinitionSoit un système dynamique , un ensemble de contraintes dans l'espace d'état et un sous-ensemble de (la cible). Le bassin de capture de (viable dans ) pour est l'ensemble des états de à partir desquels il existe au moins une évolution gouvernée par qui reste dans jusqu'à ce qu'elle atteigne la cible en temps fini. La résilience comme appartenance au bassin de capture du noyau de viabilitéSi est le noyau de viabilité de l'ensemble de contraintes pour le système , le bassin de capture de dans l'ensemble toute entier va regrouper tous les états (dans ou en-dehors) qui peuvent rejoindre le noyau de viabilité en temps fini. Si un état est dans le bassin de capture, soit il est déjà viable, soit il y a au moins une évolution à partir de cet état qui rejoint le noyau de viabilité en un temps fini. Il y a donc au moins une évolution qui part de cet état qui sera viable indéfiniment à partir de ce moment ; Donc dans le bassin de capture, si le système n'est pas viable, il pourra le devenir en temps fini. Les frontières des bassins de capture en temps inférieur à , en faisant varier , sont les courbes de niveau (isochrones) du temps minimum pour devenir viable. Elles peuvent donc servir de base à des indicateurs de résilience. Inversement, à partir d'un état qui n'est pas dans le bassin de capture du noyau de viabilité, aucune évolution ne peut rejoindre le noyau de viabilité en temps fini : le système ne sera jamais dans un état viable. Au mieux le système pourra temporairement rejoindre des états dans l’ensemble de contraintes, mais il quittera nécessairement cet ensemble en temps fini. Exemple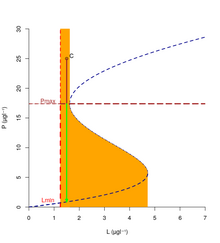 La figure 3 ci-contre montre le bassin de capture du noyau de viabilité de la figure 1 pour la dynamique (1) et l'espace tout entier. Les états en orange sont dans le noyau ou dans le bassin de capture : ce sont des états viables, ou des états à partir desquels il est possible de rejoindre un état viable en temps fini. Partout ailleurs (dans les zones blanches), il est impossible de rejoindre un état viable : au bout d'un temps fini (voir nul), le système quittera l'ensemble des contraintes (et dans cet exemple sans possibilité d'action, il ne pourra jamais y retourner). Dans le cas de la dynamique contrôlée (1)(2), le bassin de capture est l'espace tout entier : il est toujours possible de rejoindre le noyau de viabilité en temps fini (mais qui peut être très long). Gestion des incertitudesDans son exposé de la théorie de la viabilité [2], Aubin privilégie la vision d'un avenir incertain non probabilisé, comme un jeu contre la nature (en). C'est une vision ensembliste des incertitudes : les perturbations (appelées tyches) sont modélisées par des vecteurs appartenant à un ensemble. Quand la dynamique comprend des tyches, on souhaite que la viabilité soit garantie contre toutes les valeurs possibles des tyches : les évolutions doivent être viables pour toutes les valeurs que peuvent prendre les tyches. C'est la propriété de viabilité garantie. Les contraintes de viabilité ne doivent pas être violées, même en présence d'incertitudes. Les évolutions viables le sont donc dans le pire des cas, qui n'est en général pas connu à l'avance, pour des incertitudes ensemblistes (on ne sait pas, sans calcul, pour une évolution à partir d'un état donné, quelles combinaisons de contrôles et de valeurs des incertitudes amènent au pire des cas dans le futur). La théorie de la viabilité peut donc être vue comme un cadre d'implémentation du principe de précaution. Plusieurs définitions de "viabilité stochastique (en)" (au sens de bien décrite par une loi de probabilité) ont aussi été proposées, d'une part comme des solutions d'équations différentielles stochastiques viables pour presque toutes les réalisations de l'ensemble de contraintes [10] ; d'autre part, pour les systèmes à temps discret, comme probabilité pour une évolution de rester dans l'ensemble de contraintes (par exemple calculée sur la base de la proportion des réalisations qui restent dans l'ensemble de contraintes). Le noyau de viabilité stochastique peut aussi être défini pour des niveaux de confiance donnés [11]. Références
Liens externes |


![{\displaystyle K=[Lmin,+\infty [\times [0,Pmax].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7f9f775c21c5be7de120f8bb183e4bc208cd9c8)




![{\displaystyle K=[Lmin,+\infty [\times [0,Pmax]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604cd4c9005f13c3e6b9b8590da06bb0f11f37d7)




![{\displaystyle {\frac {dL}{dt}}=u\in [-u_{m},+u_{m}]\qquad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab598eb2e2de4598a0e6cc69642d9331a1fb3ce2)


