|
Squelettisation (informatique) La squelettisation est une classe d'algorithmes utilisée en analyse de forme, qui consiste à réduire une forme en un ensemble de courbes, appelées squelette, centrées dans la forme d'origine. La squelettisation est un outil d'analyse de forme non scalaire, qui conserve les propriétés topologiques de la forme d'origine ainsi que les propriétés géométriques, selon la méthode employée. Définitions et propriétésEn termes simples, la squelettisation consiste à amaigrir une forme jusqu'à obtenir un ensemble de courbes centrées. L'ensemble obtenu est alors appelé squelette ou « axe médian » (medial axis, en anglais). Il existe différentes définitions de la squelettisation. L'analogie du feu de prairieLa définition ci-dessous a été énoncée par Harry Blum et est connue sous le nom d'analogie du feu de prairie. Elle offre une vision intuitive de la squelettisation. 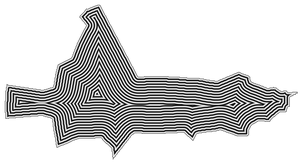
Définition formelleIl existe une définition formelle du squelette basée sur la notion de boule maximale. Le squelette d'une forme S, noté MA(S), est défini par l'ensemble des centres des boules maximales dans S: Squelette pondéréLe squelette pondéré ou la transformée de l'axe médian (medial axis transform, en anglais) d'une forme S, noté MAT(S), est l'ensemble des couples composés du centre des boules maximales de S et de leur rayon. Exosquelette et endosqueletteLes squelettes ne sont pas seulement des objets situés à l'intérieur des formes. Si nous reprenons, l'analogie du feu de prairie, le processus de squelettisation transforme non seulement l'intérieur de la forme, mais aussi l'extérieur. On appelle alors endosquelette la partie du squelette qui se situe à l'intérieur de la forme et exosquelette la partie du squelette qui se situe à l'extérieur de la forme. Il arrive souvent que la confusion soit faite entre squelette et endosquelette, car cette partie du squelette est celle qui est la plus étudiée en analyse de formes. De la même manière, dans cet article, nous considérons que les squelettes correspondent aux endosquelettes. Propriétés des squelettesLes squelettes possèdent différentes propriétés intéressantes :
D'autres propriétés sont spécifiques aux squelettes pondérés :
Une autre propriété des squelettes en général est considérée comme un défaut: la squelettisation est une transformation semi-continue. En effet, la moindre perturbation dans le contour ou au sein de la forme peut produire la création d'une branche importante dans le squelette. Méthodes de squelettisationIl existe actuellement une grande variété de méthodes permettant de construire des squelettes à partir de formes. Dans la plupart des publications scientifiques, les méthodes de squelettisation peuvent être classées selon quatre classes. Amincissement topologiqueL'amincissement topologique consiste à retirer au fur et à mesure les points du contour de la forme, tout en préservant ses caractéristiques topologiques. Les points squelettaux sont rajoutés au fur et à mesure lorsqu'il y a formation d'un coin (la courbe du contour devient discontinue) ou lorsque les points du contour se rejoignent. Extraction de la carte de distanceLa carte de distances d'une forme S consiste à associer à chaque point de S sa distance au point le plus proche du contour. Dans un cadre continu, les maxima locaux de la carte de distance correspondent exactement aux points du squelette de S. Simulation du front enflamméLes méthodes procédant par simulation du front enflammé se basent sur l'analogie du feu de prairie. Elles étudient l'évolution du front enflammé au cours du temps. Chaque formation de choc dans le front est ajouté au squelette. Calcul analytiqueLa recherche du squelette est assimilée à un problème géométrique. Les méthodes de cette classe utilisent des outils géométriques tels que les diagrammes de Voronoï ou la polygonisation du contour (dans le cas de la squelettisation dans les espaces discrets). Autres critères de classementLes méthodes de squelettisation peuvent être classées selon le type d'espace auquel elles s'appliquent. Certaines méthodes de squelettisation s'appliquent à des espaces continus. Ces méthodes sont en général exactes et précises. D'autres méthodes de squelettisation s'appliquent aux espaces discrets. Ces méthodes ne sont exactes que dans certains cas et nécessitent souvent une succession d'opérations pour affiner le squelette. Certaines méthodes de squelettisation s'appliquent à des formes sur un plan ou à des objets en trois dimensions et plus. ApplicationsLa squelettisation connaît beaucoup d'applications comme la reconnaissance de formes, la modélisation de solides pour la conception et la manipulation de formes, l'organisation de nuages de points, la recherche de chemins, les animations, etc. Elle est utilisée en médecine et en biologie depuis sa création, ainsi qu'en minéralogie. Des applications ont été trouvées dans l'indexation d'images dans les bases de données et en compression. Il existe sinon quelques applications en architecture et en urbanisme, dans le cadre d'analyse morphologique. Des chercheurs ont montré que, dans le processus de perception visuelle, notre sensibilité inconsciente est maximale au niveau du squelette. OriginesLa squelettisation est une méthode qui a été développée à l'origine dans les années soixante par Harry Blum, en vue de créer un nouveau descripteur de formes. Cette méthode a gagné l'intérêt de nombreux chercheurs. Actuellement, la squelettisation est une méthode très connue en analyse d'image. Il existe un grand nombre d'algorithmes proposant de transformer une forme en squelette. Bibliographie
|