Rondelle ressort

Représentation d'une rondelle de Belleville

Une rondelle ressort (ou rondelle élastique ou rondelle « Belleville ») est une rondelle qui assure une fonction ressort.

Ce type de ressort est fréquemment utilisé lorsque l'on souhaite une faible flexibilité sous forte charge. On le trouve couramment dans le commerce sous la désignation de « rondelle Belleville » ainsi nommée d'après son inventeur Julien Belleville[1].

Outre leur faible coût, ces rondelles ont l'avantage de pouvoir être associées de diverses manières, ce qui permet non seulement d'obtenir la raideur souhaitée pour l'ensemble, mais encore de créer des systèmes à raideur variable. Les formules donnant la résistance et la déformation de ces rondelles sont très complexes et sans intérêt pratique puisque généralement ces produits sont achetés dans le commerce. Toutefois, certaines rondelles spéciales, possédant des caractéristiques particulières, peuvent être fabriquées à la demande.

Condition de déformation

Paramétrage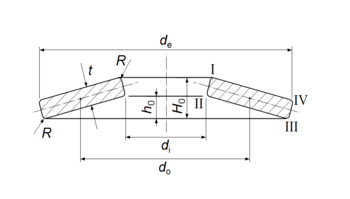

Paramétrage d'une rondelle ressort

Les principaux paramètres d'une rondelle ressort sont : son diamètre intérieur d_i, son diamètre extérieur d_e, son épaisseur t et sa hauteur à vide H₀. Dans ces conditions, sa flèche maximale sous charge vaut ${\displaystyle h_{0}\simeq H_{0}-t}$

Condition de résistance

Les rondelles ressort sont généralement calculées pour pouvoir être aplaties complètement sans se déformer plastiquement. Il existe donc une charge P, dite charge d'aplatissement, au-delà de laquelle la rondelle ne se déforme pratiquement plus. Elle peut de fait supporter des charges très élevées sans risque de rupture, à la manière d'une rondelle plate ordinaire.

On notera cependant que ces rondelles présentent, lorsqu'elles sont serrées, une circonférence intérieure travaillant en compression, et une extérieure en traction. Cette dernière est donc très sensible à l'effet d'entaille : tout défaut (fissures, oxydation…) servira d'amorce à une rupture qui se propagera de la circonférence extérieure vers l'intérieur. Comme cette surface extérieure est également la plus exposée, on évite d'employer ce montage dans des milieux sévères ou dans des applications exigeant une grande fiabilité.

Cas linéaire

Les rondelles les plus courantes ont une déformation presque linéaire, de sorte que leur raideur peut être exprimée par :

${\displaystyle k={\frac {P}{h_{0}}}}$

Formules de Almen et László

Courbe de la charge (en newtons) en fonction de la flèche imposée (en mm), calculée avec la formule de Almen et László pour différentes valeurs de h₀/t

Cependant, il est possible de fabriquer des rondelles ayant des propriétés élastiques très différentes, comme le montrent les courbes charge-flèche ci-contre en fonction du rapport h₀/t.

La force générée par la rondelle et sa raideur, ainsi que les contraintes aux arêtes peuvent être estimées par les formules ci-après[2]. Elles furent établies par J. O. Almen et A. László en 1936, alors employés de General Motors[3][4]. E et ν représentent ici le module de Young et le coefficient de Poisson respectivement.

Étant donnés :

${\displaystyle \alpha ={\frac {d_{e}}{d_{i}}}\quad ,\quad \beta ={\frac {h_{0}}{t}}}$

${\displaystyle C_{1}={\frac {1}{\pi }}{\frac {\left({\frac {\alpha -1}{\alpha }}\right)^{2}}{{\frac {\alpha +1}{\alpha -1}}-{\frac {2}{\ln \alpha }}}}}$

${\displaystyle C_{2}={\frac {1}{\pi }}{\frac {6}{\ln \alpha }}\left({\frac {\alpha -1}{\ln \alpha }}-1\right)}$

${\displaystyle C_{3}={\frac {3}{\pi }}{\frac {\alpha -1}{\ln \alpha }}}$

La force F générée à une flèche ${\displaystyle \delta }$ est donnée par la formule suivante ：

${\displaystyle F={\frac {4E}{1-\nu ^{2}}}{\frac {t^{3}}{C_{1}d_{e}^{2}}}\delta \left[\left(\beta -{\frac {\delta }{t}}\right)\left(\beta -{\frac {\delta }{2t}}\right)+1\right]}$

La raideur k de la rondelle par ：

${\displaystyle k={\frac {dF}{d\delta }}={\frac {4E}{1-\nu ^{2}}}{\frac {t^{3}}{C_{1}d_{e}^{2}}}\left[\beta ^{2}-3\beta {\frac {\delta }{t}}+{\frac {3}{2}}\left({\frac {\delta }{t}}\right)^{2}+1\right]}$

Les contraintes aux arêtes par ：

${\displaystyle \sigma _{\mathrm {I} }={\frac {4E}{1-\nu ^{2}}}{\frac {t}{C_{1}d_{e}^{2}}}\delta \left[-C_{2}\left(\beta -{\frac {\delta }{2t}}\right)-C_{3}\right]}$

${\displaystyle \sigma _{\mathrm {II} }={\frac {4E}{1-\nu ^{2}}}{\frac {t}{C_{1}d_{e}^{2}}}\delta \left[-C_{2}\left(\beta -{\frac {\delta }{2t}}\right)+C_{3}\right]}$

${\displaystyle \sigma _{\mathrm {III} }={\frac {4E}{1-\nu ^{2}}}{\frac {t}{\alpha C_{1}d_{e}^{2}}}\delta \left[(2C_{3}-C_{2})\left(\beta -{\frac {\delta }{2t}}\right)+C_{3}\right]}$

${\displaystyle \sigma _{\mathrm {IV} }={\frac {4E}{1-\nu ^{2}}}{\frac {t}{\alpha C_{1}d_{e}^{2}}}\delta \left[(2C_{3}-C_{2})\left(\beta -{\frac {\delta }{2t}}\right)-C_{3}\right]}$

Déformation de la rondelle dans le modèle de Almen et Laszlo

Et finalement le diamètre d_o du centre de rotation de la section de la rondelle (voir schéma ci-contre) ：

${\displaystyle d_{o}={\frac {d_{e}-d_{i}}{\ln \alpha }}}$

${\displaystyle \ln }$ représentant ici le logarithme népérien.

Les hypothèses utilisées dans l'établissement de ces formules sont :

• la section de la rondelle ne se déforme pas à l'écrasement, elle tourne autour d'un centre de rotation neutre dont le périmètre ne change pas ;
• l'angle de rotation φ est suffisamment petit pour négliger les termes d'ordres supérieurs ;
• la charge est uniformément repartie sur le périmètre de la rondelle, garantissant une déformation axi-symétrique[5].

Association de rondelles

Les rondelles peuvent être empilées en parallèle, ou en « paquets ». Un paquet de n rondelles identiques n'a que la flèche maximale h₀ d'une rondelle unique, mais sa charge d'aplatissement est n P ; si k est la raideur, supposée constante, d'une rondelle unique, la raideur K de l'ensemble est donc :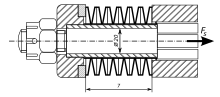

${\displaystyle K={\frac {n\,P}{h_{0}}}=n\,k}$

Exemple de montage en série

Si les rondelles sont empilées en série, ou en « opposition », la charge d'aplatissement est la même que pour une rondelle unique, mais cette fois les flèches s'ajoutent. Un empilement de n rondelles en série a donc pour raideur :

${\displaystyle K={\frac {P}{n\,h_{0}}}={\frac {k}{n}}}$

Diverses combinaisons permettent d'obtenir des ressorts aux caractéristiques presque linéaires s'ils sont réalisés avec le bon type de rondelles. Remarquons qu'il est facile d'ajuster la raideur d'un empilement contenant un nombre suffisamment important de rondelles. Par contre, la constante de raideur peut varier en fonction de la température.

Limiteur de couple constitué de deux rondelles de Belleville.

La figure ci-contre montre un limiteur de couple dans lequel l'élément élastique est constitué par deux rondelles Belleville.

D'autres dispositions sont plus subtiles. Si, par exemple, nous mettons en opposition un paquet de deux rondelles avec une rondelle unique, la flèche maximale sera 2h₀ et la charge d'aplatissement 2P, comme dans le cas précédent. Par contre, la courbe caractéristique sera une ligne brisée et non plus un segment de droite. En effet, il faut considérer deux phases distinctes lors de la compression du système :

• lorsque la charge varie de 0 à P les trois rondelles se déforment linéairement et en même temps, mais pas de la même façon : le paquet de deux rondelles se déforme deux fois moins que la rondelle unique. Lorsque la charge atteint P, la flèche vaut 1,5 h₀ car la rondelle seule se trouve complètement aplatie tandis que le paquet de deux n'est qu'à mi-course. Pendant cette phase la raideur est :

${\displaystyle K_{1}={\frac {P}{1,5\,h_{0}}}={\frac {2}{3}}k}$

• lorsque la charge varie de P à 2 P la rondelle unique est complètement aplatie et n'intervient plus, la flèche augmente de 0,5 h₀ et la raideur est celle d'un paquet de deux rondelles, soit :

${\displaystyle K_{2}=2\,k}$

Une telle association donne un ressort d'abord relativement flexible, puis très raide. On peut évidemment inventer de nombreuses autres combinaisons !

Notes et références

• (ja) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en japonais intitulé « 皿ばね » (voir la liste des auteurs).

1. (en) « Disc Springs : A Definition and Description - Belleville Springs », sur Belleville Springs (consulté le 1^er septembre 2020).
2. « Ressorts de Belleville (à disques) » (consulté le 21 septembre 2016)
3. SCHNORR 2003, p. 5.
4. (en) J. O. Almen et A. Laszlo, « The Uniform-Section Disk Spring », ASME, vol. 58,‎ 1936, p. 305-314 (lire en ligne [PDF])
5. 日本ばね学会（編） 2008, p. 272.

Articles connexes

• Ressort

Voir aussi