Problème de l'aiguille de Kakeya

Aiguille montrée en rotation à l'intérieur d'une deltoïde (qui est donc un ensemble de Kakeya). À chaque étape de sa rotation, l'aiguille est en contact avec la courbe en trois points : les deux extrémités (en bleu) et un point de tangence (en noir). Le milieu de l'aiguille (en rouge) décrit un cercle de diamètre égal à la demi-longueur de l'aiguille.

En mathématiques, et plus particulièrement en géométrie, le problème de l'aiguille de Kakeya demande l'aire minimale d'une région D du plan, telle qu'on puisse y faire tourner une aiguille (ou plus rigoureusement un segment unité) d'un tour complet ; une telle région est appelée un ensemble de Kakeya[n. 1]. Abram Besicovitch a démontré qu'il existe des ensembles de Kakeya de mesure (non nulle) aussi petite que l'on veut.

Plus généralement, un ensemble de Besicovitch est un ensemble de points d'un espace euclidien qui contient un segment de droite de longueur 1 dans chaque direction. De nombreux résultats et conjectures intéressantes concernent ces ensembles ; ainsi, Besicovitch a montré qu'il en existe de mesure nulle ; ce résultat a amené la formulation d'une conjecture plus précise, appelée conjecture de Kakeya, sur la taille minimale des ensembles de Kakeya en dimension quelconque, mais elle n'est démontrée pour l'instant que pour des espaces de petite dimension ; des généralisations de cette conjecture (en particulier aux corps finis) ont connu récemment d'importants développements.

Le problème de l'aiguille de Kakeya

Le problème de l'aiguille de Kakeya demande l'aire minimale d'une région D du plan, telle qu'on puisse y faire tourner (continûment) une aiguille (ou plus rigoureusement un segment unité) d'un tour complet[n. 2]. Cette question fut d'abord proposée, pour des régions convexes, par Sōichi Kakeya[1].

Il semble avoir suggéré que la région D d'aire minimale, sans la restriction sur la convexité, serait une deltoïde. Le problème initial (demandant que D soit convexe) fut résolu par Gyula Pál (en)[2], montrant que la solution dans ce cas est un triangle équilatéral d'aire ${\displaystyle 1/{\sqrt {3}}}$ (et donc de côté ${\displaystyle 2/{\sqrt {3}}}$ et de hauteur 1).

Ensembles de Besicovitch

Une méthode de construction d'un ensemble de Besicovitch de mesure petite par "éclatement". On montre ici deux découpages et réarrangements des pièces d'un triangle (correspondant à la description du texte pour n=1 et n=3) pour obtenir un ensemble d'aire plus petite.

Besicovitch[3] montra que l'aire d'une région D, permettant de tourner une aiguille d'un tour complet, peut être rendue aussi petite que l'on veut. Ceci développait un de ses travaux antérieurs, concernant les ensembles (à présent appelés ensembles de Besicovitch) contenant un segment unité dans chaque direction ; Besicovitch avait montré dès 1919 qu'un tel ensemble pouvait être de mesure arbitrairement petite. Il est d'ailleurs possible que le problème ait déjà été étudié auparavant.

La méthode de construction d'ensembles de Besicovitch décrite ci-dessous et illustrée sur la figure de gauche utilise des « arbres de Perron », ainsi nommés d'après O. Perron qui les utilisa pour simplifier la construction originale de Besicovitch[4] : partant d'un triangle de hauteur 1, on le divise en 2 et on translate les pièces pour que leurs bases se recouvrent partiellement. La figure ainsi obtenue contient des segments unités de mêmes directions que ceux du triangle initial passant par le sommet servant au découpage, et son aire a diminué.

Plus généralement, divisant le triangle en 2^n pièces (de bases égales), on les regroupe 2 par 2, puis 4 par 4, et ainsi de suite ; la figure ainsi obtenue ressemble à un arbre, et peut être rendue d'aire aussi petite que l'on veut. Partant d'un triangle équilatéral, et combinant trois de ces arbres (correspondants aux trois sommets du triangle), on obtient un ensemble de Besicovitch d'aire arbitrairement petite. Une adaptation de la même idée à des parallélogrammes[5] permet même d'obtenir des suites d'ensembles emboîtés ${\displaystyle K_{0}\supseteq K_{1}\supseteq K_{2}\cdots }$, dont l'intersection est par conséquent un ensemble de Besicovitch de mesure nulle.

Il existe d'autres méthodes de construction d'ensembles de Besicovitch de mesure nulle. Par exemple, Kahane[6] a utilisé des ensembles de Cantor pour construire un tel ensemble dans le plan.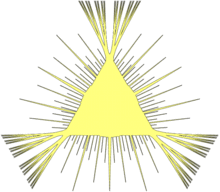

Une solution au problème de l'aiguille, construite à partir d'arbres de Perron.

Ensembles solutions du problème de l'aiguille

Utilisant une technique due à Pál (les jonctions de Pál, des ensembles de mesure arbitrairement petite permettant de déplacer continûment un segment unité entre deux lignes parallèles fixées), et partant d'un ensemble de Besicovitch formé d'arbres de Perron, on peut construire un ensemble de Kakeya (c'est-à-dire un ensemble permettant une rotation complète de l'aiguille) de mesure également aussi petite que l'on veut[7].

En 1941, H. J. Van Alphen[8] montra qu'on peut même construire des ensembles de Kakeya à l'intérieur d'un cercle de rayon ${\displaystyle 2+\epsilon }$ (où ${\displaystyle \epsilon >0}$ est arbitrairement petit).

Des ensembles de Kakeya simplement connexes d'aire plus petite que celle de la deltoïde furent trouvés en 1965. Melvin Bloom et I. J. Schoenberg construisirent indépendamment des ensembles d'aire tendant vers ${\displaystyle (5-2{\sqrt {2}})\pi /24}$ (le nombre de Bloom-Schoenberg) ; Schoenberg conjectura que cette aire ne pouvait pas être améliorée pour des ensembles simplement connexes.

Cependant, en 1971, F. Cunningham[9] montra que, pour tout ${\displaystyle \epsilon >0}$, il existe un ensemble de Kakeya simplement connexe d'aire inférieure à ${\displaystyle \epsilon }$ et contenu dans un cercle de rayon 1, ce qui est clairement le meilleur résultat possible (puisque toute rotation de l'aiguille ne peut se faire que dans un ensemble d'aire, et donc de mesure, strictement positive).

La conjecture de Kakeya

Énoncé

La question de la « taille » minimale des ensembles de Besicovitch en dimension supérieure fut alors posée, donnant naissance à un ensemble de conjectures connues comme les conjectures de Kakeya, et qui ont stimulé en partie la naissance de la théorie géométrique de la mesure. En particulier, l'existence d'ensembles de Besicovitch de mesure nulle amène naturellement à se demander s'ils pourraient également être de mesure de Hausdorff (de dimension s) nulle pour s (non nécessairement entier) strictement plus petit que la dimension de l'espace euclidien considéré. Cette question amène à la conjecture suivante :

Conjecture de Kakeya (pour les ensembles) : Soit B un ensemble de Besicovitch dans R^n (c'est-à-dire que B contient un segment unité dans chaque direction). La dimension de Hausdorff et la dimension de Minkowski de B sont alors égales à n.

Ce résultat est vrai pour n = 2 (et trivialement pour n=1), mais on ne connait que des résultats partiels en dimensions supérieures.

La fonction maximale de Kakeya

Une approche moderne de ces conjectures est d'étudier des fonctions maximales (en) particulières, construites comme suit : notant S^n-1 ⊂ R^n la sphère unité, on définit ${\displaystyle T_{e}^{\delta }(a)}$ comme étant le cylindre de longueur 1 et de rayon ${\displaystyle \delta >0}$, centré au point a ∈ R^n, et d'axe parallèle au vecteur unitaire e ∈ S^n-1. Pour une fonction localement intégrable f, on définit la fonction maximale de Kakeya de f comme étant

${\displaystyle f_{*}^{\delta }(e)=\sup _{a\in \mathbb {R} ^{n}}{\frac {1}{m(T_{e}^{\delta }(a))}}\int _{T_{e}^{\delta }(a)}|f(y)|dm(y)}$,

où m est la mesure de Lebesgue de dimension n (on remarquera que ${\displaystyle f_{*}^{\delta }}$ est une fonction définie sur les vecteurs e de la sphère S^n-1).

La conjecture suivante implique alors la conjecture de Kakeya pour les ensembles de Besicovitch :

Conjecture de Kakeya pour les fonctions maximales : Pour tout ${\displaystyle \epsilon >0}$, il existe une constante ${\displaystyle C_{\epsilon }>0}$ telle que pour toute fonction f et tout ${\displaystyle \delta >0}$, ${\displaystyle \|f_{*}^{\delta }\|_{L^{n}(\mathbf {S} ^{n-1})}\leqslant C_{\epsilon }\delta ^{-\epsilon }\|f\|_{L^{n}(\mathbf {R} ^{n})}.}$ (les normes utilisées sont celles définies dans l'article Espace Lp).

Résultats

On a démontré les résultats suivants :

• La conjecture de Kakeya est vraie pour n = 1 (trivialement) et pour n = 2 (Davies, 1971)[10].

• Dans un espace de dimension n, Wolff[11] a montré que la dimension d'un ensemble de Kakeya est au moins ${\displaystyle {\tfrac {1}{2}}}$(n+2).

• En 2002, Katz et Tao[12] ont amélioré la borne de Wolff, obtenant ${\displaystyle (2-{\sqrt {2}})(n-4)+3}$, (c'est une amélioration pour n>4).

• En 2000, Jean Bourgain obtint une relation entre le problème de Kakeya et l'arithmétique combinatoire (en)[13],[14] mettant en jeu l'analyse harmonique et la théorie additive des nombres.

Applications à l'analyse

De façon surprenante, ces conjectures ont été reliées à de nombreuses questions dans d'autres domaines, en particulier en analyse harmonique. Ainsi, en 1971, Charles Fefferman[15] utilisa une construction d'ensemble de Besicovitch pour montrer qu'en dimension supérieure à 1, des intégrales de Fourier tronquées sur des boules centrées à l'origine, de rayon tendant vers l'infini, ne convergent pas forcément en norme L^p si p ≠ 2 (contrairement à la dimension 1, où la convergence a toujours lieu).

Généralisations du problème de Kakeya

Ensembles contenant des cercles ou des sphères

Parmi les problèmes analogues au problème de Besicovitch, on a étudié des ensembles contenant des formes plus générales que des segments de droites, par exemple des cercles.

• En 1997 et 1999, Wolff a démontré[16],[17] que des sous-ensembles de R^n contenant des n-sphères de tout rayon doivent être de dimension de Hausdorff n ; sa démonstration utilise le calcul de bornes d'une fonction maximale circulaire, analogue à la fonction maximale de Kakeya.

• Une conjecture affirmant l'existence d'ensembles de mesure nulle contenant une sphère autour de chacun de leurs points fut réfutée par des résultats de Elias Stein[18] montrant que ces ensembles sont de mesure positive si n ≥ 3, et Marstrand[19], montrant le même résultat dans le cas n = 2.

Ensembles contenant des disques ou des boules

Une autre généralisation de la conjecture de Kakeya est de considérer des ensembles contenant des portions de sous-espaces de dimension k. Définissons un (n,k) -ensemble de Besicovitch K comme étant un compact de R^n de mesure nulle et contenant un translaté de tous les disques unités de dimension k (autrement dit, si B désigne la boule unité centrée en 0, pour tout sous-espace affine P de dimension k, il existe x ∈ R^n tel que ${\displaystyle (P\cap B)+x\subseteq K}$). Ainsi, les ensembles de Besicovitch définis précédemment sont les(n,1)-ensembles de Besicovitch. On a alors la

Conjecture des (n,k)-Besicovitch : il n'existe pas de (n,k)-ensembles de Besicovitch pour k>1.

En 1979, Marstrand[20] montra qu'il n'existait pas de (3,2)-ensembles de Besicovitch. Vers la même époque, Falconer[21] montra plus généralement qu'il n'existait pas de (n,k)ensembles de Besicovitch pour 2k>n. La meilleure borne actuelle est due à Bourgain[22], montrant qu'il n'existe pas de tels ensembles si 2^k-1+k>n.

Ensembles de Kakeya sur des corps finis

En 1999, Wolff proposa une conjecture analogue pour les corps finis, dans l'espoir que les techniques permettant de la résoudre pourraient se transposer au cas euclidien :

Conjecture de Kakeya pour les corps finis : Soit F un corps fini, et soit K ⊆ F^n un ensemble de Besicovitch, c'est-à-dire que pour chaque vecteur y ∈ F^n, il existe x ∈F^n tel que K contient une droite {x+ty: t ∈ F}. Alors l'ensemble K est de taille au moins c_n|F|^n, où c_n>0 est une constante ne dépendant que de n.

Zeev Dvir (en) démontra cette conjecture en 2009[23] (avec c_n = 1/n!), en utilisant ce que Terence Tao appela un "argument superbement simple"[24], de la manière suivante : Dvir observa que tout polynôme à n variables de degré inférieur à |F| s'annulant sur un ensemble de Besicovitch doit être identiquement nul. Or les polynômes à n variables de degré inférieur à |F| forment un espace vectoriel de dimension ${\displaystyle {|\mathbf {F} |+n-1 \choose n}\geq {\frac {|\mathbf {F} |^{n}}{n!}}}$.

Il y a par conséquent au moins un polynôme non trivial s'annulant sur un ensemble donné ayant moins de points que ce nombre ; combinant ces deux observations, on voit que les ensembles de Besicovitch doivent avoir au moins |F|^n/n! points. Il n'est pas clair que cette technique puisse être adaptée pour démontrer la conjecture de Kakeya dans le cas euclidien, mais cette démonstration en renforce du moins la vraisemblance, en montrant l'impossibilité de contre-exemples essentiellement construits de manière algébrique[24]. Dvir a écrit un article de synthèse sur les progrès réalisés dans le cas des corps finis (jusqu'en 2009), et leur relation à la notion d'extracteur de hasard (en)[25].

Notes et références

Notes

1. Certains auteurs anglo-saxons nomment les ensembles de Besicovitch des Kakeya sets ; les ensembles de Kakeya sont alors désignés par l'expression Kakeya needle sets (ensemble d'aiguilles de Kakeya)
2. On voit aisément qu'il suffit de pouvoir faire tourner l'aiguille d'un demi-tour, et de répéter ce déplacement ; c'est pourquoi certains auteurs définissent les ensembles de Kakeya en demandant qu'on puisse ramener l'aiguille à sa position initiale après un demi-tour, définition légèrement plus contraignante que celle utilisée ici.

Références

1. (en) Sōichi Kakeya, Some problems on maximum and minimum regarding ovals, dans Tohoku science reports (1917)
2. (da) Gyula Pál, Ueber ein elementares variationsproblem, dans Kgl. Danske Vid. Selsk. Math.-Fys. Medd. (1920)
3. A.S. Besicovitch, Sur deux questions d'intégrabilité des fonctions, dans J. Soc. Phys. Math. (1919) ; (en) On Kakeya's problem and a similar one, dansMathematische Zeitschrift (1928)
4. (de) O. Perron, « Über eine Satz von Besicovitch », Mathematische Zeitschrift, vol. 28,‎ 1928, p. 383–386 (DOI 10.1007/BF01181172)
   (en) K. J. Falconer, The Geometry of Fractal Sets, Cambridge University Press, 1985, 96–99 p.
5. Voir l'article Ensemble de Besicovitch pour une description précise de cette construction
6. (en) Jean-Pierre Kahane, « Trois notes sur les ensembles parfaits linéaires », Enseignement Math., vol. 15,‎ 1969, p. 185–192
7. (en) Markus Furtner, The Kakeya Problem
8. (nl) H. J. Alphen, « Uitbreiding van een stelling von Besicovitch », Mathematica Zutphen B, vol. 10,‎ 1942, p. 144–157
9. (en) F. Cunningham, « The Kakeya problem for simply connected and for star-shaped sets », American Mathematical Monthly, vol. 78, n^o 2,‎ 1971, p. 114–129 (lire en ligne)
10. (en) Roy Davies, « Some remarks on the Kakeya problem », Proc. Cambridge Philos. Soc., vol. 69,‎ 1971, p. 417–421 (DOI 10.1017/S0305004100046867)
11. (en) Thomas Wolff, « An improved bound for Kakeya type maximal functions », Rev. Mat. Iberoamericana, vol. 11,‎ 1995, p. 651–674 (lire en ligne)
12. (en) Nets Hawk Katz et Terence Tao, « New bounds for Kakeya problems », J. Anal. Math., vol. 87,‎ 2002, p. 231–263 (DOI 10.1007/BF02868476)
13. (en) Jean Bourgain, Harmonic analysis and combinatorics: How much may they contribute to each other ?, dans Mathematics: Frontiers and Perspectives, IMU/Amer. Math. Soc., 2000, pp. 13–32.
14. (en) Terence Tao, « From Rotating Needles to Stability of Waves: Emerging Connections between Combinatorics, Analysis and PDE », Notices of the AMS, vol. 48, n^o 3,‎ mars 2001, p. 297–303 (lire en ligne)
15. (en) Charles Fefferman, « The multiplier problem for the ball », Annals of Mathematics, vol. 94, n^o 2,‎ 1971, p. 330–336 (DOI 10.2307/1970864, JSTOR 1970864)
16. (en) Thomas Wolff, « A Kakeya-type problem for circles », American Journal of Mathematics, vol. 119,‎ 1997, p. 985–1026 (DOI 10.1353/ajm.1997.0034)
17. (en) Thomas Wolff et Lawrence Kolasa, « On some variants of the Kakeya problem », Pacific Journal of Mathematics, vol. 190,‎ 1999, p. 111–154 (lire en ligne)
18. (en) Elias Stein, « Maximal functions: Spherical means », Proc. Natl. Acad. Sci. USA, vol. 73, n^o 7,‎ 1976, p. 2174–2175 (PMID 16592329, PMCID 430482, DOI 10.1073/pnas.73.7.2174)
19. (en) J. M. Marstrand, « Packing circles in the plane », Proc. London. Math. Soc., vol. 55,‎ 1987, p. 37–58 (DOI 10.1112/plms/s3-55.1.37)
20. (en) J. M. Marstrand, « Packing Planes in R^3 », Mathematika, vol. 26,‎ 1979, p. 180–183 (DOI 10.1112/S0025579300009748)
21. (en) K. J. Falconer, « Continuity properties of k-plane integrals and Besicovitch sets », Math. Proc. Cambridge Philos. Soc., vol. 87,‎ 1980, p. 221–226 (DOI 10.1017/S0305004100056681)
22. (en) Jean Bourgain, « Besicovitch type maximal operators and applications to Fourier analysis », Geom. Funct. Anal., vol. 1,‎ 1997, p. 147–187 (DOI 10.1007/BF01896376)
23. (en) Zeev Dvir, « On the size of Kakeya sets in finite fields », Journal of the American Mathematical Society, vol. 22, n^o 4,‎ 2009, p. 1093–1097 (lire en ligne)
24. (en) Terence Tao, « Dvir’s proof of the finite field Kakeya conjecture », What's New, 24 mars 2008 (consulté le 8 avril 2008)
25. (en) Zeev Dvir, From Randomness Extraction to Rotating Needles, dans Electronic Colloquium on Computational Complexity (2009)

Voir aussi

• Ensemble de Besicovitch

Références

• (en) Abram Besicovitch, « The Kakeya Problem », American Mathematical Monthly, vol. 70, n^o 7,‎ 1963, p. 697–706 (DOI 10.2307/2312249, JSTOR 2312249)
• (en) F. Cunningham, « The Kakeya problem for simply connected and for star-shaped sets », American Mathematical Monthly, vol. 78, n^o 2,‎ 1971, p. 114–129 (lire en ligne)
• (en) Zeev Dvir, « On the size of Kakeya sets in finite fields », Journal of the American Mathematical Society, vol. 22, n^o 4,‎ 2009, p. 1093–1097 (DOI 10.1090/S0894-0347-08-00607-3, MR 2525780, arXiv 0803.2336)
• (en) K. J. Falconer, The Geometry of Fractal Sets, Cambridge University Press, 1985
• (en) Soichi Kakeya, « Some problems on maximum and minimum regarding ovals », Tohoku science reports, vol. 6,‎ 1917, p. 71–88
• (en) Nets Hawk Katz, Izabella Łaba et Terence Tao, « An improved bound on the Minkowski dimension of Besicovitch sets in R^3 », Ann. Of Math., vol. 152, n^o 2,‎ 2000, p. 383–446 (lire en ligne)
• (en) Thomas Wolff, Prospects in Mathematics, AMS, 1999, « Recent work connected with the Kakeya problem »
• (en) Thomas Wolff, Lectures in Harmonic Analysis, AMS, 2003

Liens externes

• Kakeya at University of British Columbia
• Besicovitch at UCLA
• Kakeya needle problem at mathworld

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Kakeya set » (voir la liste des auteurs).