Polynôme de Macdonald

En mathématiques, les polynômes de Macdonald P_λ(x; t,q) sont une famille de polynômes symétriques orthogonaux à plusieurs variables, introduite par Ian G. Macdonald en 1987. Il en a ensuite introduit une généralisation non symétrique en 1995. Macdonald associait à l'origine ses polynômes à des poids λ de systèmes de racines finis et utilisait une seule variable t, mais il s'est rendu compte plus tard qu'il était plus naturel de les associer à des systèmes de racines affines plutôt qu'à des systèmes de racines finis, ce qui permet de remplacer la variable t par plusieurs variables différentes t =(t₁,..., t_k), une pour chacune des k orbites de racines dans le système de racines affines. Les polynômes de Macdonald sont des polynômes à n variables x =(x₁,..., x_n), où n est le rang du système de racines affines. Ils généralisent de nombreuses autres familles de polynômes orthogonaux, telles que les polynômes de Jack, les polynômes de Hall-Littlewood et les polynômes d'Askey-Wilson, qui eux-mêmes incluent la plupart des polynômes orthogonaux à une variable nommés comme cas particuliers. Les polynômes de Koornwinder sont des polynômes de Macdonald pour certains systèmes de racines non réduits. Ils ont des relations profondes avec les algèbres de Hecke affines et les schémas de Hilbert, qui ont été utilisés pour prouver plusieurs conjectures faites par Macdonald à leur sujet.

Définition

Fixons d'abord quelques notations.

• R est un système de racines fini dans un espace vectoriel réel V.
• R^+ est un ensemble de racines positives, auquel correspond une chambre de Weyl positive.
• W est le groupe de Weyl de R.
• Q est le réseau des racines de R (le réseau engendré par les racines).
• P est le réseau des poids de R (il contient Q).
• Un ordre sur les poids : ${\displaystyle \mu \leq \lambda }$ si et seulement si ${\displaystyle \lambda -\mu }$ est une combinaison linéaire de racines simples à coefficients entiers positifs.
• P^+ est l'ensemble des poids dominants : ce sont les éléments de P dans la chambre de Weyl positive.
• ρ est le vecteur de Weyl, i.e. la demi-somme des racines positives ; c'est un élément particulier de P^+ à l'intérieur de la chambre de Weyl positive.
• F est un corps de caractéristique 0, généralement le corps des nombres rationnels.
• A = F(P) est l'algèbre de groupe de P, muni d'une base d'éléments notée e^λ pour λ ∈ P.
• Si ${\displaystyle f=e^{\lambda }}$, alors ${\displaystyle {\overline {f}}}$ signifie ${\displaystyle e^{-\lambda }}$, et cette notation est étendue par linéarité à toute l'algèbre de groupe.
• ${\displaystyle m_{\mu }=\sum _{\lambda \in W\mu }e^{\lambda }}$ est une somme sur une orbite ; ces éléments forment une base de la sous-algèbre A^W des éléments fixés par W.
• ${\displaystyle (a;q)_{\infty }=\prod _{r\geq 0}(1-aq^{r})}$ est le q-symbole de Pochhammer infini.
• ${\displaystyle \Delta =\prod _{\alpha \in R}{(e^{\alpha };q)_{\infty } \over (te^{\alpha };q)_{\infty }}.}$
• ${\displaystyle \langle f,g\rangle =({\text{terme constant de }}f{\overline {g}}\Delta )/|W|}$ est le produit scalaire de deux éléments de A, du moins lorsque t est une puissance entière positive de q.

Définition par orthogonalisation de Gram-Schmidt

Les polynômes de Macdonald ${\displaystyle P_{\lambda }}$ pour ${\displaystyle \lambda \in P^{+}}$ sont caractérisés par les deux conditions suivantes :

• ${\displaystyle P_{\lambda }=\sum _{\mu \leq \lambda }u_{\lambda \mu }m_{\mu }}$ où ${\displaystyle u_{\lambda \mu }}$ est une fonction rationnelle de q et t avec ${\displaystyle u_{\lambda \lambda }=1}$ ;
• ${\displaystyle P_{\lambda }}$ et ${\displaystyle P_{\mu }}$ sont orthogonaux si ${\displaystyle \lambda <\mu }$.

Caractérisation comme vecteurs propres d'un opérateur auto-adjoint

Soit ${\displaystyle \Lambda _{n,F}=\Lambda _{n}\otimes _{\mathbb {Z} }F}$ l'anneau gradué de polynômes symétriques avec ${\displaystyle n}$ indéterminée et coefficients sur ${\displaystyle F=\mathbb {Q} (q,t)}$ le corps des fonctions rationnelles en ${\displaystyle q}$ et ${\displaystyle t}$.

Pour $i$ entier naturel, soit ${\displaystyle T_{q,x_{i}}}$ l'opérateur de décalage défini par

${\displaystyle f(x_{1},\dots ,x_{n})\mapsto f(x_{1},\dots ,x_{i-1},qx_{i},x_{i+1},\dots ,x_{n})}$.

Macdonald commence en fait par définir[1] « ses » polynômes de Macdonald ${\displaystyle P_{\lambda }}$ sont des vecteurs propres convenablement normalisés de l'opérateur auto-adjoint ${\displaystyle D:\Lambda _{n,F}\to \Lambda _{n,F}}$

${\displaystyle D=\sum \limits _{i=1}^{n}\prod \limits _{i\neq j}{\frac {(tx_{i}-x_{j})}{(x_{i}-x_{j})}}T_{q,x_{i}}}$

avec pour valeurs propres, deux à deux distinctes, ${\displaystyle \sum \limits _{i=1}^{n}q^{\lambda _{i}}t^{n-i}}$. Il montre ensuite que les ${\displaystyle P_{\lambda }}$ sont caractérisés par les deux conditions du paragraphe précédent.

Commentaire sur la première définition

En d'autres termes, les polynômes de Macdonald sont obtenus en orthogonalisant la base évidente de A^W. L'existence de polynômes avec ces propriétés est facile à montrer (pour tout produit scalaire). Une propriété clé des polynômes de Macdonald est qu'ils sont orthogonaux : ${\displaystyle \langle P_{\lambda },P_{\mu }\rangle =0}$ si ${\displaystyle \lambda \neq \mu }$. Ce n'est pas une conséquence triviale de la définition car ${\displaystyle P^{+}}$ n'est pas totalement ordonné, et possède donc de nombreux éléments incomparables. Il faut ainsi vérifier que les polynômes correspondants sont toujours orthogonaux. L'orthogonalité peut être prouvée en montrant que les polynômes de Macdonald sont des vecteurs propres pour une algèbre d'opérateurs auto-adjoints qui commutent entre eux et qui ont des espaces propres de dimension un, et en utilisant le fait que les espaces propres pour différentes valeurs propres sont orthogonaux.

Dans le cas de systèmes de racines non simplement lacés (B, C, F, G), on peut faire dépendre le paramètre t de la longueur de la racine, ce qui donne lieu à une famille à trois paramètres de polynômes de Macdonald. On peut aussi étendre la définition au système de racines non réduit BC, auquel cas on obtient une famille à six paramètres (un t pour chaque orbite de racines, plus q) appelée polynômes de Koornwinder. Il est parfois préférable de considérer les polynômes de Macdonald comme dépendant d'un système de racines affine, éventuellement non réduit. Dans ce cas, il y a un paramètre t associé à chaque orbite de racines dans le système de racines affines, plus un paramètre q. Le nombre d'orbites de racines peut varier de 1 à 5.

Exemples

• Si q = t, les polynômes de Macdonald deviennent les caractères de Weyl des représentations du groupe compact associé au système de racines, ou les fonctions de Schur dans le cas des systèmes de racines de type A.
• Si q = 0, les polynômes de Macdonald deviennent les fonctions sphériques zonales (renormalisées) pour un groupe p-adique semi-simple, ou les polynômes de Hall-Littlewood lorsque le système de racines est de type A.
• Si t = 1, les polynômes de Macdonald deviennent les sommes sur les orbites de W, qui sont les fonctions symétriques des monômes lorsque le système racine est de type A.
• Si on pose t = q^α et que q tend vers 1, les polynômes de Macdonald deviennent des polynômes de Jack lorsque le système de racines est de type A, et des polynômes de Heckman–Opdam pour les systèmes de racines plus généraux.
• Pour le système de racines affines A₁, les polynômes de Macdonald sont les polynômes de Rogers.
• Pour le système de racines affine non réduit de rang 1 de type (C
  ₁, C₁), les polynômes de Macdonald sont les polynômes d'Askey–Wilson, qui à leur tour incluent comme cas particuliers la plupart des familles nommées de polynômes orthogonaux à 1 variable.
• Pour le système racinaire affine non réduit de type (C
  _n, C_n), les polynômes de Macdonald sont les polynômes de Koornwinder.

La conjecture du terme constant de Macdonald

Si t = q ^k pour un entier positif k, alors la norme des polynômes de Macdonald est donnée par

${\displaystyle \langle P_{\lambda },P_{\lambda }\rangle =\prod _{\alpha \in R,\alpha >0}\prod _{0<i<k}{1-q^{(\lambda +k\rho ,2\alpha /(\alpha ,\alpha ))+i} \over 1-q^{(\lambda +k\rho ,2\alpha /(\alpha ,\alpha ))-i}}.}$

Cela a été conjecturé par Macdonald (1982) comme une généralisation de la conjecture de Dyson, et démontré pour tous les systèmes de racines (réduits) par Cherednik (1995) en utilisant les propriétés des algèbres de Hecke doublement affines (DAHA). La conjecture avait auparavant été prouvée par plusieurs auteurs au cas par cas pour tous les systèmes de racines, sauf ceux de type E_n.

Il existe deux autres conjectures qui, avec la conjecture de la norme, sont collectivement appelées les conjectures de Macdonald dans ce contexte : en plus de la formule de la norme, Macdonald a conjecturé une formule pour la valeur de P_λ au point t^ρ, et une symétrie

${\displaystyle {\frac {P_{\lambda }(\dots ,q^{\mu _{i}}t^{\rho _{i}},\dots )}{P_{\lambda }(t^{\rho })}}={\frac {P_{\mu }(\dots ,q^{\lambda _{i}}t^{\rho _{i}},\dots )}{P_{\mu }(t^{\rho })}}.}$

À nouveau, ces conjectures ont été démontrées pour les systèmes de racines réduits généraux par Cherednik (1995) en utilisant les algèbres de algèbres de Hecke doublement affines ; la démonstration a été étendue au cas BC peu de temps après par des travaux de van Diejen, Noumi et Sahi.

La conjecture de positivité de Macdonald

Dans le cas des systèmes de racines de type ${\displaystyle A_{n-1}}$, les polynômes de Macdonald sont simplement des polynômes symétriques à n variables avec des coefficients qui sont des fonctions rationnelles de q et t. Une version légèrement modifiée ${\displaystyle {\widetilde {H}}_{\mu }}$ des polynômes de Macdonald (voir la formule combinatoire ci-dessous) forment une base orthogonale de l'espace des fonctions symétriques sur ${\displaystyle \mathbb {Q} (q,t)}$, et peut donc être exprimé en termes de fonctions de Schur ${\displaystyle s_{\lambda }}$. Les coefficients K_λμ(q, t) de ces relations sont appelés les coefficients de Kostka-Macdonald ou coefficients qt-Kostka. Macdonald a conjecturé que les coefficients de Kostka-Macdonald sont des polynômes en q et t dont les coefficients sont des entiers naturels. Ces conjectures sont maintenant démontrées ; l'étape la plus difficile, la dernière, a été de prouver la positivité, ce qui a été fait par Mark Haiman (2001), en prouvant la « conjecture n! »[2].

C'est toujours un problème ouvert central en combinatoire algébrique de trouver une formule combinatoire pour les coefficients qt-Kostka.

La conjecture n!

La conjecture n! d'Adriano Garsia et Mark Haiman stipule que pour chaque partition μ de n l'espace

${\displaystyle D_{\mu }=C[\partial x,\partial y]\,\Delta _{\mu }}$

engendrée par toutes les composées de dérivées partielles de

${\displaystyle \Delta _{\mu }=\det(x_{i}^{p_{j}}y_{i}^{q_{j}})_{1\leq i,j,\leq n}}$

est de dimension n!, où (p_j, q_j) parcourt les n éléments du diagramme de la partition μ, considérée comme un sous-ensemble des couples d'entiers naturels. Par exemple, si μ est la partition 3 = 2 + 1 sur n = 3 alors les couples (p_j, q_j) possibles sont (0, 0), (0, 1), (1, 0), et l'espace D _μ est engendré par

${\displaystyle \Delta _{\mu }=x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}}$

${\displaystyle y_{2}-y_{3}}$

${\displaystyle y_{3}-y_{1}}$

${\displaystyle x_{3}-x_{2}}$

${\displaystyle x_{1}-x_{3}}$

${\displaystyle 1}$

qui est de dimension 6 = 3!.

La démonstration de Haiman de la conjecture de positivité de Macdonald et de la conjecture n! consistait à montrer que le schéma de Hilbert isospectral (en) de n points dans le plan était de Cohen-Macaulay (et même Gorenstein). Des résultats antérieurs de Haiman et Garsia avaient déjà montré que cela impliquait la conjecture n! et que la conjecture n! impliquait que les coefficients de Kostka-Macdonald sont des multiplicités de caractères gradués pour les modules D_μ. Cela entraîne immédiatement la conjecture de positivité de Macdonald car les multiplicités de caractères sont nécessairement des entiers naturels.

Ian Grojnowski et Mark Haiman ont trouvé une autre démonstration de la conjecture de positivité de Macdonald en prouvant une conjecture de positivité pour les polynômes LLT.

Formule combinatoire pour les polynômes de Macdonald

En 2005, J. Haglund, M. Haiman et N. Loehr[3] ont donné la première preuve d'une interprétation combinatoire des polynômes de Macdonald. En 1988, I. G. Macdonald[4] a donné la seconde preuve d'une interprétation combinatoire des polynômes de Macdonald (équations (4.11) et (5.13)). La formule de Macdonald est différente de celle de Haglund, Haiman et Loehr, avec beaucoup moins de termes (cette formule est également prouvée dans l'ouvrage fondateur de Macdonald[5], dans le chapitre VI (7.13)). Bien que très utiles pour le calcul et intéressantes en soi, ces formules combinatoires n'impliquent pas immédiatement la positivité des coefficients de Kostka-Macdonald ${\displaystyle K_{\lambda \mu }(q,t),}$ car elles donnent la décomposition des polynômes de Macdonald dans la base des fonctions symétriques monomiales et pas celle des fonctions de Schur.

Écrites en termes de polynômes de Macdonald transformés ${\displaystyle {\widetilde {H}}_{\mu }}$ plutôt que les plus habituels ${\displaystyle P_{\lambda }}$, elles sont

${\displaystyle {\widetilde {H}}_{\mu }(x;q,t)=\sum _{\sigma \,:\,\mu \to \mathbb {Z} _{+}}q^{\mathrm {inv} (\sigma )}t^{\mathrm {maj} (\sigma )}x^{\sigma }}$

où σ est un remplissage du diagramme de Young de forme μ, inv et maj sont certaines statistiques combinatoires (fonctions) définies sur le remplissage σ. Cette formule est une expression des polynômes de Macdonald en une infinité de variables. Pour obtenir les polynômes en n variables, il suffit de restreindre la formule aux remplissages qui n'utilisent que les entiers 1, 2,..., n. Le terme x^σ doit être interprété comme ${\displaystyle x_{1}^{\sigma _{1}}x_{2}^{\sigma _{2}}\cdots }$ où σ_i est le nombre de cases dans le remplissage de μ qui ont le contenu i.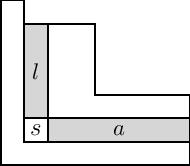

La figure représente le bras et la jambe d'une case d'un diagramme de Young. Le bras est le nombre de cases à sa droite et la jambe est le nombre de cases au-dessus.

Les polynômes de Macdonald modifiés ${\displaystyle {\widetilde {H}}_{\mu }(x;q,t)}$ dans la formule ci-dessus sont reliés aux polynômes de Macdonald classiques ${\displaystyle P_{\lambda }}$ via une suite de transformations. Premièrement, la forme intégrale des polynômes de Macdonald, notée ${\displaystyle J_{\lambda }(x;q,t)}$, est une renormalisation de ${\displaystyle P_{\lambda }(x;q,t)}$ qui efface les dénominateurs des coefficients :

${\displaystyle J_{\lambda }(x;q,t)=\prod _{s\in D(\lambda )}(1-q^{a(s)}t^{1+l(s)})\cdot P_{\lambda }(x;q,t)}$

où ${\displaystyle D(\lambda )}$ est l'ensemble des cases du diagramme de Young de ${\displaystyle \lambda }$, et ${\displaystyle a(s)}$ et ${\displaystyle l(s)}$ désignent le bras et la jambe du carré ${\displaystyle s}$, comme indiqué sur la figure. Remarque : la figure ci-contre utilise la notation française pour le tableau, qui est inversée verticalement par rapport à la notation anglaise utilisée sur la page Wikipédia pour les diagrammes de Young. La notation française est plus couramment utilisée dans l'étude des polynômes de Macdonald.

Les polynômes de Macdonald modifiés ${\displaystyle {\widetilde {H}}_{\mu }(x;q,t)}$ peut alors être défini en termes des ${\displaystyle J_{\mu }}$. On a en effet

${\displaystyle {\widetilde {H}}_{\mu }(x;q,t)=t^{-n(\mu )}J_{\mu }\left[{\frac {X}{1-t^{-1}}};q,t^{-1}\right]}$

où

${\displaystyle n(\mu )=\sum _{i}\mu _{i}\cdot (i-1).}$

Les crochets ci-dessus indiquent une substitution pléthystique (en).

Cette formule peut être utilisée pour démontrer la formule de Knop et Sahi sur les polynômes de Jack.

Polynômes de Macdonald non symétriques

En 1995, Macdonald a introduit un analogue non symétrique des polynômes de Macdonald symétriques, et les polynômes de Macdonald symétriques peuvent facilement être retrouvés à partir de la version non symétrique. Dans sa définition originale, il caractérise les polynômes de Macdonald non symétriques comme une famille unique de polynômes orthogonaux pour un certain produit scalaire et qui satisfont à une propriété de triangularité lorsqu'ils sont développés dans la base des monômes.

En 2007, Haglund, Haiman et Loehr ont donné une formule combinatoire pour les polynômes de Macdonald non symétriques.

Les polynômes de Macdonald non symétriques se spécialisent en caractères de Demazure en prenant q = t = 0, et en polynômes clés lorsque q = t = ∞.

Formules combinatoires basées sur le processus d'exclusion

En 2018, S. Corteel, O. Mandelshtam et L. Williams ont utilisé le processus d'exclusion pour donner une caractérisation combinatoire directe des polynômes de Macdonald, à la fois les symétriques et les non symétriques[6]. Leurs résultats diffèrent des travaux antérieurs de Haglund en partie parce qu'ils donnent directement une formule pour les polynômes de Macdonald plutôt qu'une transformation de ceux-ci. Les autrices développent le concept d'une file d'attente multiligne, qui est une matrice contenant des boules ou des cellules vides, ainsi qu'une application entre les boules et leurs voisines et un mécanisme d'étiquetage combinatoire. Le polynôme de Macdonald non symétrique s'écrit alors :

${\displaystyle E_{\lambda }({\textbf {x}};q,t)=\sum _{Q}\mathrm {wt} (Q)}$

où la somme porte sur toutes les files d'attente multilignes ${\displaystyle L\times n}$ de type ${\displaystyle \lambda }$ et ${\displaystyle \mathrm {wt} }$ est une fonction de pondération qui associe des polynômes spécifiques à ces files d'attente. Le polynôme de Macdonald symétrique, lui, est :

${\displaystyle P_{\lambda }({\textbf {x}};q,t)=\sum _{\mu }E_{\mu }(x_{1},...,x_{n};q,t)=\sum _{\mu }\sum _{Q}\mathrm {wt} (Q)}$

où la somme extérieure porte sur toutes les compositions distinctes ${\displaystyle \mu }$ qui sont des permutations de la partition ${\displaystyle \lambda }$, et la somme intérieure est la même que ci-dessus.

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Macdonald polynomials » (voir la liste des auteurs).

1. (en) I. G. Macdonald, « A new class of symmetric functions », Séminaire lotharingien de combinatoire, Universität Wien, Fakultät für Mathematik, vol. 20,‎ 1988, p. 143-145 (ISSN 1286-4889, lire en ligne).
2. Mark Haiman, « Hilbert schemes, polygraphs, and the Macdonald positivity conjecture », Journal of the American Mathematical Society, vol. 14, n^o 4,‎ 2001, p. 941–1006 (DOI 10.1090/S0894-0347-01-00373-3 , Bibcode 2000math.....10246H, arXiv math.AG/0010246, S2CID 9253880).
3. J. Haglund, M. Haiman et N. Loehr, « A combinatorial formula for Macdonald polynomials », Journal of the American Mathematical Society, vol. 18, n^o 3,‎ 2005, p. 735-761 (ISSN 0894-0347, DOI 10.1090/S0894-0347-05-00485-6 , MR 2138143)
4. Macdonald, I. G. A new class of symmetric functions. Publ. I.R.M.A. Strasbourg, 1988, 372/S–20 Actes 20^e Séminaire Lotharingien, p. 131–171. eudml.org
5. Macdonald, I. G. Symmetric functions and Hall polynomials. Second edition. Oxford Mathematical Monographs. Oxford Science Publications. The Clarendon Press, Oxford University Press, New York, 1995. x+475 pp. (ISBN 0-19-853489-2), lien Math Reviews.
6. Sylvie Corteel, Olya Mandelshtam et Lauren Williams, « From multiline queues to Macdonald polynomials via the exclusion process », American Journal of Mathematics, vol. 144,‎ 2022, p. 395-436 (arXiv 1811.01024)

Bibliographie

• Ivan Cherednik, « Double Affine Hecke Algebras and Macdonald's Conjectures », Annals of Mathematics, second Series, vol. 141, n^o 1,‎ 1995, p. 191-216 (ISSN 0003-486X, DOI 10.2307/2118632, JSTOR 2118632)
• Adriano Garsia et Jeffrey B. Remmel, « Breakthroughs in the theory of Macdonald polynomials », PNAS, vol. 102, n^o 11,‎ 15 mars 2005, p. 3891-3894 (PMID 15753285, PMCID 554818, DOI 10.1073/pnas.0409705102 , Bibcode 2005PNAS..102.3891G)
• Mark Haiman Combinatorics, symmetric functions, and Hilbert schemes Current Developments in Mathematics 2002, no. 1 (2002), 39-111.
• Haiman, Mark Notes on Macdonald polynomials and the geometry of Hilbert schemes. Symmetric functions 2001 : surveys of developments and perspectives, 1-64, NATO Sci. Ser. II Math. Phys. Chem., 74, Kluwer Acad. Publ., Dordrecht, 2002, lien Math Reviews.
• Mark Haiman, « Hilbert schemes, polygraphs, and the Macdonald positivity conjecture », J. Amer. Math. Soc., vol. 14, n^o 4,‎ 2001, p. 941-1006 (DOI 10.1090/S0894-0347-01-00373-3, arXiv math.AG/0010246, S2CID 9253880)
• A. A. Kirillov, « Lectures on affine Hecke algebras and Macdonald's conjectures », Bull. Amer. Math. Soc., vol. 34, n^o 3,‎ 1997, p. 251-292 (DOI 10.1090/S0273-0979-97-00727-1 , lire en ligne)
• I. G. Macdonald, « Some conjectures for root systems », SIAM Journal on Mathematical Analysis, vol. 13, n^o 6,‎ 1982, p. 988-1007 (ISSN 0036-1410, DOI 10.1137/0513070, MR 674768)
• I. G. Macdonald, Symmetric functions and Hall polynomials, New York, The Clarendon Press, Oxford University Press, coll. « Oxford Mathematical Monographs », 1995, 2^e éd., x+475 (ISBN 0-19-853489-2, MR 1354144)
• I. G. Macdonald, Symmetric functions and orthogonal polynomials : Dean Jacqueline B. Lewis Memorial Lectures presented at Rutgers University, New Brunswick, NJ, vol. 12, Providence, RI, American Mathematical Society, coll. « University Lecture Series », 1998, xvi+53 (ISBN 0-8218-0770-6, MR 1488699)
• Macdonald, I. G. Affine Hecke algebras and orthogonal polynomials. Séminaire Bourbaki 797 (1995).
• I. G. Macdonald, « Orthogonal polynomials associated with root systems », Séminaire Lotharingien de Combinatoire, vol. 45,‎ 2000-2001, Art. B45a (MR 1817334, arXiv math.QA/0011046)
• I. G. Macdonald, Affine Hecke algebras and orthogonal polynomials, vol. 157, Cambridge, Cambridge University Press, coll. « Cambridge Tracts in Mathematics », 2003, x+175 (ISBN 978-0-521-82472-9, MR 1976581)

Liens externes

• La page de Mike Zabrocki sur les polynômes de Macdonald.
• Certains des articles de Haiman sur les polynômes de Macdonald.