|
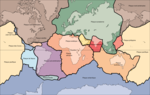
Point triple (géodynamique)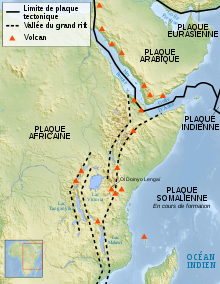 Un point triple (ou parfois, par analogie avec le terme anglais, jonction triple[1]) désigne, en tectonique des plaques, une région où trois plaques tectoniques se rejoignent[2]. Une jonction quadruple est théoriquement possible, mais ne peut exister que transitoirement[3]. Pour l'analyse théorique, au voisinage d'un point triple (ou jonction triple), la limite entre deux plaques tectoniques peut être de trois formes : une dorsale, une fosse ou une faille transformante. Sur les nombreuses combinaisons possibles, seules quelques-unes sont stables sans condition (c'est-à-dire que la configuration n'évoluera pas pendant des durées géologiques) ; et de nombreuses configurations imposent des conditions géométriques sur les frontières ou sur les déplacements des plaques. L'étude de ces stabilités et des contraintes qu'elles imposent sur les directions des frontières permet de mieux caractériser le mouvement relatif des plaques, ou de prédire l'évolution de points triples instables au fil des temps géologiques. Géométriquement, l'effacement d'une frontière entre deux plaques supprimant deux points triples, il y a donc (approximativement) deux fois plus de points triples qu'il n'y a de plaques prises en compte dans le modèle. La croûte terrestre présentant une vingtaine de plaques significatives, on peut donc y recenser une quarantaine de points triples significatifs ; mais les micro-plaques en introduisent en réalité beaucoup plus. Étude de la stabilité des points triples • Au nord, la Jonction triple de Mendocino est de type TFF. • Au sud, la Jonction triple de Rivera est de type RTF. HistoriqueLe premier article scientifique sur le concept de point triple en tectonique des plaques a été publié en 1969 par William Jason Morgan, Dan Peter McKenzie, et Tanya Atwater[4]. Le terme a été initialement employé pour décrire l'intersection de trois dorsales, ou frontières de divergence. Selon la théorie, lors de la rupture d'un continent, trois limites divergentes se forment, partant d'un point central (la triple jonction). Ces trois limites forment idéalement un angle de 120° à leur point de rencontre. Une de ces frontières de plaque divergentes finit par avorter (aulacogène), et les deux autres continuent à se séparer pour former un océan. Ainsi, l'ouverture de l'océan Atlantique sud a débuté au sud des continents sud-américain et africain, à partir d'un point triple situé dans l'actuel golfe de Guinée, d'où elle s'est poursuivie vers l'ouest. Le fossé de la Bénoué et le rift d'Afrique centrale, orientés vers le NE, constituent le bras avorté de cette jonction[5]. Par la suite, le terme « point triple » en est venu à désigner d'une manière générale tout point de rencontre entre trois plaques tectoniques. Hypothèses simplificatricesLes propriétés des triples jonctions se décrivent plus facilement en se limitant à un point de vue purement cinématique, en supposant que les plaques sont rigides et se déplacent à la surface de la Terre. Aucune connaissance de l'intérieur de la Terre ou des détails géologiques de la croûte terrestre n'est alors nécessaire. Une autre simplification utile vient de ce que la cinématique des triples jonctions sur une Terre plate est essentiellement la même que celle de la surface d'une sphère. En supposant que les plaques sont rigides et que la Terre est sphérique, on peut appliquer le théorème de Leonhard Euler sur le mouvement d'une surface rigide sur une sphère. Sur une sphère, les mouvements de la plaque sont décrits comme des rotations relatives autour des pôles d'Euler (voir tectonique des plaques). Le mouvement relatif en chaque point le long d'une limite de la plaque peut être calculé à partir de cette rotation. L’hypothèse de rigidité s’applique très bien dans le cas de la croûte océanique, et les convergences ou divergences de croûtes continentales cessent rapidement à l'échelle de temps géologique. Par ailleurs, le rayon de la terre à l’équateur et aux pôles ne varie que d’un facteur de 300 environ, si bien que la terre se rapproche très bien d’une sphère. McKenzie et Morgan ont commencé l'analyse de la stabilité des jonctions triples[6] à l'aide de ces hypothèses, en prenant comme hypothèse supplémentaire que les pôles d'Euler décrivant les mouvements des plaques étaient tels qu'ils se rapprochaient du mouvement rectiligne sur une surface plane. Cette simplification s'applique lorsque les pôles d'Euler sont distants de la triple jonction concernée, ce qui permet de réduire l’évaluation de la stabilité d'un point triple à la détermination des limites et des mouvements relatifs des plaques en interaction. Ainsi, l'analyse des jonctions triples peut généralement se faire en la modélisant sur une surface plane, par des mouvements définis par des vecteurs. Cette simplification peut être appliquée à la plupart des triples jonctions actuelles, du moment que les hypothèses s'appliquent suffisamment bien à la situation réelle de la Terre. On peut décrire les triples jonctions et évaluer leur stabilité sans utiliser les détails géologiques, mais simplement en définissant les propriétés des dorsales, des fosses et des failles transformantes concernées, en faisant des hypothèses simplificatrices et en appliquant des calculs de vitesse simples. La zone autour d'une triple jonction est suffisamment petite (par rapport à la taille de la sphère) et (généralement) suffisamment éloignée du pôle de rotation pour que le mouvement relatif entre deux plaques puisse être supposé constant le long de leur bordure commune. Sur le plus long terme, il n'est pas possible (sauf cas particulier) que les pôles eulériens d'un système de trois plaques restent fixes au cours du mouvement, si bien que les directions des vitesses aux points triples vont en réalité varier continuement[7] à de très grandes échelles de temps géologiques. L'approximation est cependant suffisante pour caractériser le fonctionnement typique à moyen terme des différents points triples. Représentation de l'espace des vitessesNB : Dans ce qui suit, il convient de bien distinguer entre l'espace géographique des trois plaques A, B, C et de leurs frontières (AB), (BC) et (CA) ayant un point commun P, et l'espace de représentation des vitesses avec le triangle et la vitesse de déplacement du point triple représentée par . Pour cette représentation géométrique[8] on suppose que toutes les vitesses sont constantes, tant celles des plaques que celle du point triple. Si trois plaques A, B et C sont en déplacement les unes par rapport aux autres, on peut représenter ces déplacements relatifs par un triangle tel que représente le déplacement de B vu d'un point de A, et de même pour et . Sur ce même graphique, qui forme l'espace de représentation des vitesses, on peut représenter de même le déplacement d'un point P se déplaçant par rapport à l'une ou l'autre plaque, en reportant sa vitesse de déplacement par rapport à la plaque A. De la composition des vitesses relatives, il vient immédiatement que représentera sa vitesse de déplacement par rapport à B, et de même pour C. Supposons à présent que le déplacement des trois plaques est stable, et que le point P est le point triple de rencontre de ces trois plaques, défini dynamiquement comme le point de rencontre à un instant donné de la frontière commune (AB) de A et B, (BC) de B et C, et (CA) de C et A. Localement, ces trois frontières sont trois demi-droites issues du point P. Vu de la plaque A, le point P doit évidemment rester en permanence sur la frontière (AB), mais peut se déplacer le long de cette frontière, vers la droite ou la gauche au fil du temps, en fonction de l'évolution relative de la plaque C. Ceci étant posé, la nature (R, T ou F) de chaque frontière va imposer une condition sur les positions possibles pour ce point . Trois types de frontières En tectonique des plaques, les plaques ont des mouvements relatifs variés, ce qui génère entre elles trois types de frontières : convergentes, divergentes ou transformantes. Les limites des plaques restant actives sur le long terme, à l'échelle de temps géologique, sont des dorsales océaniques divergentes (R), les zones de subduction convergentes (T), et les failles transformantes (F). Les définitions utilisées pour modéliser les limites de type R, T et F sont les suivantes :
Cas d'une crête océanique (R) Dans le cas d'un rift océanique entre A et B, la configuration géologiquement stable est celle où le déplacement relatif est perpendiculaire à la frontière commune (AB) des deux plaques, et la vitesse de formation de la croûte océanique est la même de part et d'autre du rift. Vu de la plaque A, la vitesse du point P peut s'analyser suivant deux composantes, l'une parallèle à la frontière (AB) et l'autre parallèle au déplacement . Vu de la plaque A, pour que le point P reste en permanence sur la frontière (AB), sa composante de vitesse parallèle à la frontière peut être quelconque, mais dans la direction perpendiculaire la vitesse d'éloignement doit être la moitié de . Par conséquent, par rapport au triangle dans l'espace de représentation des vitesses, le point représentant la vitesse de déplacement du point triple devra se situer sur la médiatrice du segment . Cas d'une faille transformante (F) Dans le cas d'une faille transformante entre A et B, la configuration géologiquement stable est celle où le déplacement relatif est parallèle à la frontière commune (AB) des deux plaques, faute de quoi la frontière se transformerait à long terme en rift ou en zone de subduction. Pour que le point P reste en permanence sur la frontière (AB), sa composante de vitesse parallèle à la frontière et au vecteur peut être quelconque, mais dans l'autre direction, il doit nécessairement rester sur la frontière, et sa vitesse de déplacement est donc nécessairement nulle. Par conséquent, par rapport au triangle dans l'espace des vitesses, le point devra dans ce cas se situer sur la droite passant par et . De plus, on peut noter que dans ce cas, la direction de la frontière (AB) est donc la même que celle de . Noter cependant que dans ce cas, la position relative des deux plaques de part et d'autre de la frontière n'est pas directement déterminée, conduisant potentiellement à deux solutions dans l'espace géologique suivant que la faille transformante est lévogyre ou dextrogyre. Géologiquement, il n'y a que peu de limites de plaques qui correspondent à une faille transformante. L'exemple le plus important est la grande transformante entre la plaque nord américaine et la plaque du Pacifique, qui se traduit localement par la célèbre faille de San Andreas, en bordure de la croûte continentale de la plaque nord-américaine. En contexte océanique, des failles transformantes se trouvent sur la plaque caraïbe, et sur la plaque Scotia, au sud de la plaque sud-américaine. Cas d'une fosse de subduction (T) Dans le cas d'une zone de subduction convergente, la configuration géologiquement stable est celle faisant par exemple passer le plancher océanique de B sous la plaque A (qui peut être une croûte continentale ou océanique), la plaque B disparaissant progressivement, alors que A ne varie pas sensiblement dans sa frontière. Vu de la plaque A, pour que le point reste en permanence sur la frontière (AB), sa composante de vitesse parallèle à la frontière peut être quelconque, mais elle doit être nulle dans la direction perpendiculaire. Par conséquent, par rapport au triangle , le point représentatif de la vitesse devra se situer sur une droite passant par , et de même direction que la frontière (AB), quelle qu'elle soit. Noter que dans ce cas, la position de A et B est inversée entre le schéma géologique et le schéma des vitesses. Il y a géométriquement deux configurations possibles pour une subduction, suivant que par rapport au point triple la plaque recouvrante A progresse dans le sens des aiguilles d'une montre, ou dans le sens trigonométrique[7]. Géologiquement, une zone de subduction borde souvent un arc insulaire ou une croûte continentale, il est rare d'en trouver des exemples entre deux croûtes océaniques, et impossible d'en avoir une instance entre deux croûtes continentales (la zone est alors une zone statique d'orogénèse). Lorsque la zone de subduction s'enfonce sous de la croûte continentale, la frontière de la subduction est en pratique déterminée par la limite de la croûte continentale associée. Les quelques zones de subduction océanique (plaque caraïbe, plaque des Sandwich, mais surtout l'est de la plaque australienne) ne dessinent pas de point triple très significatif en leurs extrémités. Condition de stabilité sur le point tripleUne jonction stable est une jonction dont la géométrie se conserve dans le temps, au fur et à mesure du déplacement des plaques, c'est-à-dire que les différentes frontières conservent leur nature et leur orientation relative par rapport au point triple. Cela impose des restrictions sur les vitesses relatives et l’orientation des limites de la plaque. Une triple jonction instable, au contraire, se transformera pour devenir une autre forme de triple jonction (les jonctions RRF, entre deux rifts et une faille transformante, évolueront facilement en jonctions FFR, entre deux failles transformantes et un rift), changera de géométrie ou ne sera tout simplement pas réalisable (comme un point de rencontre entre trois failles transformantes). Chaque frontière impose sa propre condition sur la position du point dans l'espace de représentation des vitesses, sous forme d'une droite traduisant cette condition. Le point se situera donc à l'intersection de ces droites, quand elle existe ; et la configuration sera instable sinon. On voit immédiatement, par exemple, que :
McKenzie et Morgan ont déterminé qu'il existait théoriquement 16 types de triples jonctions possibles, bien que plusieurs d'entre eux sont spéculatifs et n'ont pas nécessairement été vus sur la Terre. McKenzie et Morgan ont avancé que 14 de ces configurations étaient stables, les configurations FFF et RRF étant en revanche instables. Cependant, York[9] a par la suite montré que la configuration RRF pouvait être stable dans certaines conditions. De son côté, Cronin[7] identifie 25 types de combinaisons, dont 19 peuvent être stables. Cette analyse théorique s'applique essentiellement aux points triples rencontrés dans la croûte océanique. Les limites de plaques dans la croûte continentale sont beaucoup plus diffuses et donnent généralement lieu à des phénomènes géologiques beaucoup plus complexes. Même dans ce cas, les hypothèses faites sur l'évolution des différents types de frontières ne sont qu'approximatives ; elles sont cependant suffisantes pour fournir une caractérisation au premier ordre de la dynamique de ces points[7]. Typologie de points triples Les jonctions peuvent être classées d’une part en fonction des types de limites de plaques rencontrées (dix types possibles : RRR, RRF, RRT, RFF, RFT, RTT, FFF, FFT, FTT, TTT) et, d’autre part, en fonction du sens de déplacement relatif des plaques concernées : une faille transformante peut être lévogyre ou sinistrogyre, et vue depuis le point triple une subduction peut être celle de la plaque de gauche ou de droite. Certaines configurations telles que RRR ne peuvent avoir qu'un seul ensemble de mouvements relatifs alors que les jonctions TTT peuvent être classées en TTT (a) et TTT (b). Ces différences de direction du mouvement affectent les critères de stabilité. La nature d'un point triple ne se déduit pas simplement du mouvement relatif des plaques qui le portent. Si les fosses de subduction sont généralement homogènes et bien marquées, les dorsales sont ponctuées de nombreuses failles de décrochement ; et les rares plaques globalement en décrochement ont leurs limites ponctuées de nombreuses anomalies de compression ou d'extension. D'autre part, si la limite des plaques reste relativement visible dans les croûtes océaniques, elle devient très brouillée dans les zones continentales. Triple divergence (RRR)  Dans le triangle des vitesses, la contrainte sur les trois côtés est que la vitesse représentative du point triple se trouve à l'intersection des trois médianes. Un tel point existe toujours, et l'intersection peut donc toujours être stable. On peut noter cependant que l'intersection ne se situe pas nécessairement à l'intérieur du triangle des vitesses, si l'un de ses angles est obtus. Une jonction RRR suivant ces définitions est toujours stable, et est donc très commune sur Terre, bien que sur le plan géologique, la divergence de l'une des dorsales sera généralement interrompue dans une direction, laissant la zone de rift en échec. Il existe de nombreux exemples de ce type, à la fois aujourd'hui et dans le passé géologique, tels que l'ouverture de l'Atlantique Sud avec des crêtes s'étendant au nord et au sud pour former la dorsale médio-atlantique et un aulacogène associé dans la région du delta du Niger en Afrique. L'autre raison pour laquelle les jonctions RRR sont courantes est que la divergence suivant trois fractures à 120 ° est le meilleur moyen de résorber les contraintes imposées lors du soulèvement de la surface d'une sphère. Sur la Terre, on pense que des stress similaires à ceux-ci sont causés par les points chauds du manteau, qui sont censés initier la division des continents. Les points triples de type RRR sont nombreux à la surface du globe :
La mer du Nord est située sur l'emplacement d'un point triple fossile du Jurassique, au large de l'Écosse, jonction de trois plaques continentales du Paléozoïque : Avalonia, Laurentia and Baltica[10],[11]. L'étude d'un point triple de ce type montre qu'il n'est pas rigoureusement stable à long terme, et évolue transitoirement en un point de type RRF[12]. Dans la mesure où une dorsale océanique n'est pas faite que de dorsales mais présente une alternance de crêtes et de failles transformantes, cette instabilité pourrait être une des explications à la création périodique de failles transformantes à partir d'un point triple RRR. Deux dorsales et une faille (RRF)  Un point triple de rencontre entre deux dorsales et une faille est généralement instable, et n'existe que transitoirement, par exemple au moment où le décrochement atteint une dorsale et consacre la séparation de deux nouvelles plaques. Il dégénère alors normalement en un point triple de type RFF, le point de raccordement se déplaçant sur une faille de décrochement de la dorsale primitive. Il peut également exister comme instabilité transitoire d'un point triple de type RRR, le point triple ouvrant transitoirement une faille transformante avant de reprendre sa forme RRR structurelle. Géométriquement, le triangle représentatif des vitesses des plaques pour un point de type RRF est en effet très contraint : la vitesse du point triple doit se situer pour deux des côtés à l'intersection de deux médiatrices (contrainte R), et être également situé sur le troisième côté (contrainte F). Cette condition ne peut théoriquement être réalisée de manière stable que si le triangle des vitesses est rectangle, et que les deux crêtes forment un angle droit, la faille décrochante équilibrant exactement les vitesses. Sur la base de mouvements à grande échelle des plaques, les triples jonctions attendues croisant deux dorsales et une faille transformante (RRF) sont la Jonction triple des Açores, à la jonction de la dorsale médio-atlantique, orienté nord-sud, et du rift de Terceira, orienté ouest-est, celle de la plaque Juan Fernández entre la transformante du Chili et la dorsale est-pacifique, et la triple jonction Aden-Owen-Carlsberg (en) (AOC) au sud de la plaque arabique, point de contact des plaques somalienne et indienne. Dans ces deux premiers cas, cependant, la jonction n'existe pas sous forme de point triple, mais forme une micro-plaque en expansion[13] La dernière se situe dans une zone fortement perturbée, et semble être actuellement une forme de transition entre une forme RFF primitive et une forme de type RRR[13]. La Jonction triple de Macquarie, au sud-est de l'Australie, était à sa formation une jonction de type RRF, la Dorsale sud-est indienne se prolongeant vers le sud par la Dorsale Pacifique-Antarctique, et une faille transformante est-ouest, la faille de Macquarie établissant la (future) limite entre la plaque Pacifique et la plaque antarctique. Ce point triple a été déstabilisé il y a une trentaine de millions d'années, à la suite d'un changement dans le déplacement relatif entre l’Antarctique et le Pacifique. Le point triple est à présent positionné sur une faille de décrochement est-ouest, ce qui en fait un point de type RFF. Deux dorsales et une fosse (RRT) Un point triple entre deux dorsales et une fosse pourrait géométriquement exister et être stable, mais est géologiquement très peu probable. Comparé à un point triple de type RRR, où les trois plaques divergent du point triple par trois dorsales, on peut réaliser géométriquement un point triple de type RRT en découpant dans l'espace géographique une des dorsales et son prolongement sur l'autre plaque, et en imposant aux deux lèvres ainsi formées un mouvement supplémentaire de convergence inversant celui de la dorsale, ce qui soude de facto la frontière des deux plaques primitivement séparées par cette dorsale et créé au contraire une fosse de subduction sur la troisième, dans le prolongement de l'ex-dorsale. Cette construction étant faite, on voit qu'on a bien réalisé un point triple de type RRT, mais la géométrie des vitesses impose donc que la plaque portant les deux dorsales forme un angle rentrant sur ce point triple. Deux failles et une dorsale (RFF)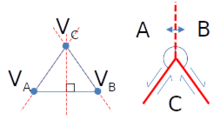     La géométrie d'un point triple RFF impose que dans le triangle représentatif des vitesses, celle du point triple doit être à la fois sur la médiatrice d'un des côtés (R) et sur les deux autres (F). Ceci peut être réalisé dans deux cas, conduisant à deux types possibles de points triples RFF :
Un exemple du premier type est la Jonction triple de Bouvet, probablement instable sur le long terme. Structurellement, ce point triple est celui où la dorsale atlantique vient rencontrer la plaque antarctique. Structurellement, les trois frontières sont des crêtes océaniques, formées d'alternances de failles d'expansion et de failles de décrochement. On s'attendrait donc à un point triple de type RRR dans une position stable. Cependant, les vitesses relatives des plaques sont à peu près symétriques par rapport à la plaque antarctique, permettant ici de terminer la dorsale médio-atlantique sur deux failles de décrochement formant un angle rentrant du côté de la plaque antarctique. L'équilibre des vitesses pour conserver un triangle isocèle étant difficile à assurer, c'est en pratique cette dernière condition qui peut se rencontrer dans la nature : une crête océanique qui vient se terminer à angle droit d'une faille de décrochement. Il y a peu d'exemples de ce type, dans la mesure où une faille de décrochement est une limite rare entre deux plaques. Un premier exemple est celui de la faille transformante de la bordure sud de la Plaque des Sandwich et de la plaque Scotia, qui rencontre une dorsale à la limite de ces deux plaques. C'est à présent le cas de la Jonction triple de Macquarie, primitivement de type RRF. Il semblerait que ça ait été primitivement le cas de la triple jonction Aden-Owen-Carlsberg (en) (AOC) au sud de la plaque arabique, point de contact des plaques somaliennes et indiennes, et point d'achèvement de la dorsale de Carlsberg qui parcourt l'océan Indien. Un exemple probable de point triple de ce type est constitué par la faille transformante séparant la plaque sud-américaine de la Plaque caraïbe et de la plaque des Andes du Nord, ces deux dernières étant séparées par une faille d'extension à angle droit de la transformante. Le point triple est situé sur la côte du Vénézuela, à l'ouest de Caracas, là où la côte sensiblement est-ouest (sur la faille transformante) prend une direction nord-sud (sur la faille d'extension). Un cas dégénéré important de la rencontre entre deux failles transformantes et une dorsale est celui de l'intersection entre un segment « actif » d'une dorsale océanique et la faille transformante qui la relie au segment suivant, laquelle est active vers le segment suivant et passive de l'autre côté. Une telle intersection n'est évidemment pas celle de trois plaques actives, puisque l'une des frontières est statique ; mais sa description mathématique relève directement du cas où le triangle des vitesses est dégénéré. Dans ce cas limite, la dégénérescence est double, puisque deux vitesses de déplacement sont identiques ; le « triangle » des vitesses se réduit alors à un simple segment. Faille, dorsale et fosse (RFT)   Un point triple associant faille transformante, dorsale et fosse océanique peut être de deux types, suivant que la plaque en subduction est celle bordée par la faille transformante ou par la dorsale.
La jonction triple au nord de la plaque Rivera a été historiquement du premier type. La plaque Rivera est un fragment nord se détachant de la plaque des Cocos, elle-même le reliquat sud de la plaque Farallon, qui a presque totalement disparu par subduction sous le continent américain au Jurassique. La limite entre l'ex-plaque Farallon et la plaque nord-américaine est la fin de la fosse de subduction d'Amérique centrale, et au-delà du point triple le contact entre la plaque nord-américaine et la plaque pacifique correspond à la faille de San Andreas, dans le prolongement de la fosse précédente. La frontière entre plaque des Cocos et la plaque Pacifique étant une divergence, le point triple est bien de type RFT, et la plaque en subduction (ici celle de Rivera) est bordée par la dorsale est-Pacifique. Cependant, la géologie de la zone est très perturbée par la rupture survenue d'avec la plaque des Cocos ; et il semble que le point triple soit en voie de transformation vers un classique RRR. Un autre exemple est peut-être la jonction triple de la Reine-Charlotte, au large du Canada, où l’extrémité nord de la plaque Explorer marque la fin de la zone de subduction de Cascadia. Deux fosses et une dorsale (RTT) On trouve ce type de triple jonction près de l’île Moresby, dans l’ouest de l’Amérique du Nord.
Dans leur mouvement de subduction sous les Andes, les prolongements des deux plaques de Nazca et de l'Antarctique continuent de diverger sous la plaque sud-américaine, mais l'écart croissant entre les plaques n'est plus compensé par l'apport de manteau refroidi par l'océan et formant de la croûte océanique froide. Par conséquent, sous la subduction d'une dorsale, l’asthénosphère va être en contact direct avec la croûte superficielle, en en modifiant le régime thermique[14]. Trois failles (FFF) Il s'agit d'une jonction de trois faille transformante. Bien que cette formule soit instable, on en trouve deux exemples en Anatolie, aux deux extrémités de la faille est-anatolienne, située dans l'est de la Turquie, qui forme la limite entre les plaques anatolienne et arabique : Deux failles et une fosse (FFT)La Jonction triple de Mendocino, à l’extrémité nord de la faille de San Andreas, Deux fosses et une faille (FTT)Il existe une de ces triple jonctions au large des côtes chiliennes: Trois fosses (TTT) Un point triple de rencontre entre trois fosses peut théoriquement correspondre à deux configurations : soit l'une des plaques est en position de subduction par rapport aux deux autres, soit chacune est en subduction par rapport à sa voisine (de droite ou de gauche). Cette dernière configuration est instable. Le type stable se rencontre au large du Japon, au niveau d'Osaka : la triple jonction de Boso est le lieu de rencontre des plaques du Pacifique à l'est, qui s'enfonce sous celle de la mer Phillippine au sud, les deux étant en subduction par rapport à celle d’Okhotsk au nord. Sur ce point triple, la fosse du Japon (au nord) se poursuit par la fosse d'Izu-Ogasawara (au sud) ; la convergence entre sud et nord étant en revanche peu marquée. Sur la terre ferme, le mont Fuji est situé à une triple jonction de convergence, où se rejoignent la Plaque de l'Amour (plaque eurasienne), la plaque d'Okhotsk (plaque nord-américaine) et la plaque marine des Philippines[15],[16]. Ces trois plaques forment respectivement la partie occidentale du Japon, la partie orientale du Japon et la péninsule d'Izu.
Références
AnnexesLiens externesArticles connexes |







![{\displaystyle \scriptstyle [AB]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62bd5fa0fc22264b6d844a31706ca0037a0903d0)