|
Ordre de mériteL'ordre de mérite (en anglais : merit order), ou préséance économique, est un moyen de classer les sources d'énergie à disposition pour la production d'électricité, selon l'ordre croissant du prix (qui peut refléter l'ordre de leurs coûts marginaux de production à court terme) et parfois de la pollution à cause des quotas d'émissions du CO2. Dans une gestion centralisée, le classement fait en sorte que ceux qui ont les coûts marginaux les plus bas sont les premiers à être mis en ligne pour répondre à la demande, et les usines avec les coûts marginaux les plus élevés sont les dernières à être appelées. Cette répartition de la production minimise le coût de production de l'électricité. Parfois, les unités de production doivent être démarrées sans tenir compte de l'ordre de mérite, en raison de la congestion du transport, de la fiabilité du système ou pour d'autres raisons[1]. Cette logique économique intègre le prix des quotas de CO2, ce qui privilégie les énergies à bas carbone. L'ordre d'appel économique correspondait à l'ordre croissant des émetteurs de CO2 jusqu'à ce que le prix du gaz augmente en Europe à la suite des sanctions européennes contre le gaz russe et fasse devenir le charbon plus avantageux économiquement que le gaz[2]. 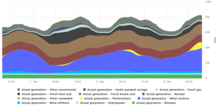 Formulation mathématique de baseCe qui suit repose sur les travaux suivants : Biggar et Hesamzadeh (2014) [3] et Kirschen (2010)[4]. Le problème de répartition économique peut être considéré comme la maximisation du bénéfices économique W d'un réseau électrique tout en respectant les contraintes du système. Pour un réseau à n bus (nœuds), supposons que Sk est le taux de génération, et Dk est le taux de consommation au bus k. Supposons, en outre, que Ck(Sk) est la fonction de coût de la production d'électricité (c'est-à-dire le taux auquel le générateur encourt des coûts lorsqu'il produit au taux Sk ), et Vk(Dk) est le taux auquel le la charge reçoit de la valeur ou des avantages (exprimés en unités monétaires) lorsqu'elle consomme au taux Dk. Le bien-être total est alors La tâche de répartition économique consiste à trouver la combinaison des taux de production et de consommation ( Sk, Dk ) qui maximise cette expression W sous réserve d'un certain nombre de contraintes : La première contrainte, qui est nécessaire pour interpréter les contraintes qui suivent, est que l'injection nette à chaque bus est égale à la production totale à ce bus moins la consommation totale : La contrainte d'équilibre de puissance impose que la somme des injections nettes sur tous les bus soit égale aux pertes de puissance dans les branches du réseau : Les pertes de puissance L dépendent des débits dans les branches et donc des injections nettes comme le montre l'équation ci-dessus. Cependant il ne peut pas dépendre des injections sur tous les bus car cela donnerait un système surdéterminé. Ainsi un bus est choisi comme bus Slack et est omis des variables de la fonction L. Le choix du bus Slack est entièrement arbitraire, ici le bus n est choisi. La deuxième contrainte concerne les contraintes de capacité sur le débit sur les lignes du réseau. Pour un système à m lignes, cette contrainte est modélisée comme suit : où Fl est le débit sur la branche l, et Flmax est la valeur maximale que ce débit est autorisé à prendre. Notez que l'injection nette au niveau du bus de mou n'est pas incluse dans cette équation pour les mêmes raisons que ci-dessus. où π et μ sont les multiplicateurs lagrangiens des contraintes. Les conditions d'optimalité sont alors : où la dernière condition est nécessaire pour gérer la contrainte d'inégalité sur la capacité de la ligne. La résolution de ces équations est difficile sur le plan informatique car elles sont non linéaires et impliquent implicitement la solution des équations de flux de puissance. L'analyse peut être simplifiée à l'aide d'un modèle linéarisé appelé flux de puissance CC. Il existe un cas particulier que l'on retrouve dans une grande partie de la littérature. C'est le cas où la demande est supposée parfaitement inélastique (c'est-à-dire insensible au prix). Cela revient à supposer que pour une très grande valeur de et demande inélastique . Sous cette hypothèse, le bien-être économique total est maximisé en choisissant . La tâche de répartition économique se réduit à : Sous réserve de la contrainte que et les autres contraintes énoncées ci-dessus. Répartition environnementaleDans la répartition environnementale, des considérations supplémentaires concernant la réduction de la pollution compliquent davantage le problème de répartition de l'énergie. Les contraintes de base du problème de répartition économique restent en place, mais le modèle est optimisé pour minimiser les émissions de polluants en plus de minimiser les coûts de carburant et la perte de puissance totale[2]. En raison de la complexité supplémentaire, un certain nombre d'algorithmes ont été utilisés pour optimiser ce problème de répartition environnemental/économique. Notamment, un algorithme d'abeilles modifié mettant en œuvre les principes de modélisation chaotique a été appliqué avec succès non seulement in silico, mais également sur un système de modèles physiques de générateurs[2]. D'autres méthodes utilisées pour résoudre le problème économique de répartition des émissions comprennent l'optimisation de l'essaim de particules (PSO) et les réseaux de neurones Une autre combinaison notable d'algorithmes est utilisée dans un outil d'émissions en temps réel appelé Localisational Emissions Estimation Methodology (LEEM) qui relie la consommation d'énergie électrique et les émissions de polluants qui en résultent[5]. Le LEEM estime les changements d'émissions associés aux changements incrémentiels de la demande d'électricité à partir des informations sur les prix marginaux localisés (LMP) des gestionnaires de réseau indépendants (ISO) et des données sur les émissions de l'Agence américaine de protection de l'environnement (EPA)[5]. LEEM a été développé à la Wayne State University dans le cadre d'un projet visant à optimiser les systèmes de transport d'eau à Detroit, MI à partir de 2010 et a depuis trouvé une application plus large en tant qu'outil de gestion du profil de charge qui peut aider à réduire les coûts de production et les émissions[6]. Notes et références
Voir aussiLiens externesBibliographie
Articles connexes
|





![{\displaystyle {\mathcal {L}}=\sum _{k=1}^{n}C_{k}(I_{k})+\pi \left[L(I_{1},I_{2},\dots ,I_{n-1})-\sum _{k=1}^{n}I_{k}\right]+\sum _{l=1}^{m}\mu _{l}\left[F_{l}^{max}-F_{l}(I_{1},I_{2},\dots ,I_{n-1})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a61b0798363b176fbb66560afbeedc767089654b)



![{\displaystyle \mu _{l}\cdot \left[F_{l}^{max}-F_{l}(I_{1},I_{2},\dots ,I_{n-1})\right]=0\quad \mu _{l}\geq 0\quad k=1,\dots ,n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7177da319002628918a4222112b2a626b3083d0)





