Modèle matriciel de population

Un modèle matriciel de population est un modèle mathématique permettant de décrire la dynamique d'une population structurée en classes. Cela signifie que, sous réserve que les individus de la population puissent être groupés en catégories au sein desquelles les probabilités de survie et les taux de reproduction sont les mêmes pour tout individu, ces modèles peuvent être utilisés pour prédire l'évolution du nombre d'individus présents dans chaque catégorie d'un pas de temps sur l'autre (typiquement, d'une année sur l'autre).

La forme générale des modèles matriciels de population est :

${\displaystyle \mathbf {n} (t+1)=\mathbf {A\,n} (t)}$

où n(t) est un vecteur dont les composantes correspondent au nombre d'individus dans les différentes classes du modèle, et A est une matrice à coefficients positifs. Un modèle matriciel de population peut donc être vu comme une extension du modèle de croissance géométrique de Malthus permettant de prendre en compte le fait que les individus d'une population ne sont pas tous identiques.

Un des principaux avantages de ces modèles est leur grande simplicité. Elle en fait des outils important pour l'écologie théorique mais aussi pour des domaines plus appliqués comme la biologie de la conservation ou la démographie humaine.

Historique

L'utilisation de modèles matriciels pour décrire des dynamiques de populations a été introduite plusieurs fois de façon indépendante : par Harro Bernardelli en 1941[1], par E. G. Lewis en 1942[2] et Patrick H. Leslie en 1945[3],[4]. Les travaux de Leslie étant les plus aboutis et ceux qui ont eu le plus d'influence, c'est lui qui est généralement crédité pour l'introduction des modèles matriciels de population en biologie.

Les modèles considérés par Leslie se limitaient à une structuration de la population en classes d'âge. En 1965, Leonard Lefkovitch introduisit une classification par stades développementaux[5]. Un modèle structuré en classes de taille fut introduite l'année suivante par Michael B. Usher[6]. D'autres structurations furent introduites par la suite, comme la structuration selon la position géographique utilisée dans les modèles de métapopulations. Aujourd'hui, même s'il est clair que les modèles matriciels de population peuvent être généralisés à toute structure discrète de population, les modèles en classes d'âge et en classes de taille restent les plus fréquents en pratique.

Expression mathématique du modèle

Forme générale

Préliminaire : le modèle de Malthus

Le modèle de croissance géométrique de Malthus s'écrit :

${\displaystyle n(t+1)=\lambda \,n(t)}$

où n(t) est le nombre d'individus au temps t et λ est le taux de croissance géométrique de la population, qui correspond à la contribution d'un individu présent dans la population au temps t à la constitution de la population au temps t + 1. Une récurrence immédiate permet d'obtenir une formule explicite pour la taille de la population :

${\displaystyle n(t)=\lambda ^{t}\,n(0)}$

Ainsi, on voit que la population suit une dynamique géométrique et croît (resp. décroît) lorsque λ > 1 (resp. λ < 1).

Une des limites de ce modèle est qu'il ne prend pas en compte une éventuelle structure de la population : son interprétation biologique repose sur le fait que tous les individus ont la même probabilité de survie d'un pas de temps sur l'autre et le même taux de reproduction, hypothèse peu satisfaisante dans beaucoup de cas. L'intérêt des modèles matriciels est de relâcher cette hypothèse.

Le modèle matriciel de population

Une façon simple de prendre en compte les différences entre les individus est de les grouper en classes au sein desquelles les caractéristiques démographiques sont homogènes. On généralise ensuite le modèle de Malthus en considérant la contribution d'un individu de classe j à la composition de la classe i au pas de temps suivant. En notant cette contribution a_ij, on peut écrire que la contribution totale de la classe j à la classe i sera a_ij n_j(t), où n_j(t) est l'effectif de la classe j au temps t (c'est-à-dire le nombre d'individus qui la composent). En sommant sur toutes les classes, on obtient l'effectif de la classe i au temps t + 1 :

${\displaystyle n_{i}(t+1)=\sum _{j}a_{ij}\,n_{j}(t)}$

d'où le système :

${\displaystyle {\begin{cases}n_{1}(t+1)&=a_{11}\,n_{1}(t)+\cdots +a_{1m}\,n_{m}(t)\\&\vdots \\n_{m}(t+1)&=a_{m1}\,n_{1}(t)+\cdots +a_{mm}\,n_{m}(t)\\\end{cases}}}$

Ce système peut être écrit sous forme matricielle :

${\displaystyle \mathbf {n} (t+1)=\mathbf {A\,n} (t)}$

Le vecteur n = (n_i) est appelé vecteur population est la matrice A = (a_ij) est appelée matrice de projection de la population. De cette expression, on déduit la formule explicite

${\displaystyle \mathbf {n} (t)=\mathbf {A} ^{t}\mathbf {n} (0)}$

Ainsi, en connaissant le vecteur population initial n(0), on peut déduire la taille de la population pour tout temps t ∈ ℕ en itérant un produit matriciel.

Lien avec les chaînes de Markov

L'expression précédente est la forme générale des modèles matriciels de population. On peut remarquer qu'à une transposée près, ce formalisme est identique à celui utilisé pour étudier les chaînes de Markov, x_t+1 = x_tP. La principale différence entre les matrices de projections de population et les matrices de transition des chaînes de Markov est que la somme des entrées des colonnes de A ne vaut pas 1. Ceci est dû au fait que les individus peuvent mourir (la somme peut donc être inférieure à 1) et se reproduire (la somme peut donc être supérieure à 1). Une autre différence est que, dans le cas des matrices de projection de population, on ne s'intéresse le plus souvent qu'à des matrices possédant des propriétés supplémentaires (primitivité) — par exemple, la présence d'un état absorbant (étudiée en chaîne de Markov) n'est pas pertinente d'un point de vue biologique.

Interprétation biologique

Interprétation des entrées de la matrice

Un individu peut contribuer à la composition de la population au pas de temps suivant de deux manières :

• en survivant
• en produisant de nouveaux individus

la contribution a_ij d'un individu de la classe j à la composition de la classe i correspond donc à la somme de deux termes :

${\displaystyle a_{ij}=s_{ij}+f_{ij}}$

où s_ij est la probabilité qu'un individu observé dans la classe j au temps t soit observé dans la classe i au temps t + 1, et f_ij est le nombre moyen d'individus de classe i produits par un individu de classe j (lorsque le modèle est female-based, il s'agit du nombre moyen de femelles produites). Ceci permet de décomposer la matrice A en

${\displaystyle \mathbf {A=S+F} }$

La matrice S est appelée matrice de survie et la matrice F est appelée matrice de fertilité. Cette décomposition est utilisée pour calculer de nombreux descripteurs (taux net de reproduction, temps de génération, espérance de vie...) de la population en construisant une chaîne de Markov modélisant les trajectoires des individus dans le cycle de vie au cours de leur vie à partir de S. Cela permet d'utiliser de nombreux résultats de la théorie des chaînes de Markov absorbantes.

Graphe du cycle de vie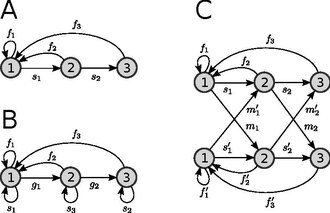

Figure 1 : exemples de cycles de vie fréquemment rencontrés dans l'étude des modèles matriciels de population : (A) classes d'âge; (B) classes de taille; (C) métapopulation (deux populations structurées en classes d'âge).

Cette section emploie certains mots issus de la théorie des graphes (« orienté », « pondéré », « sommet », « arc ») dont vous pourrez trouver (si besoin est) la définition précise dans le lexique de la théorie des graphes.

Les modèles matriciels de population peuvent être représentés de façon naturelle au moyen d'un graphe orienté et pondéré. Pour cela, on associe à chaque classe un sommet et à chaque transition un arc de la manière suivante : à une entrée a_ij non nulle de la matrice de projection de la population est associé un arc de poids a_ij allant du sommet j au sommet i. Un tel graphe est appelé graphe du cycle de vie.

Cette représentation présente plusieurs avantages. Par exemple, elle permet de formaliser la notion de cycle de vie, centrale en biologie. Enfin, certaines questions sont plus naturelles à traiter en raisonnant sur des graphes que sur des matrices – comme en témoigne le fait que la caractérisation de certaines propriétés importantes (irréductibilité, apériodicité – cf section sur le comportement asymptotique) est plus simple en termes de graphes qu'en termes de matrices, ou encore l'utilité de méthodes comme la réduction de graphe[7].

Modèles basés sur les femelles

Les modèles matriciels de population ne permettent pas de prendre en compte les interactions entre les individus (la contribution d'un individu de classe j à la composition de la classe i, a_ij, est constante et ne dépend pas du nombre d'individus dans les différentes classes du modèle). C'est cette hypothèse qui garantit la linéarité du modèle et empêche l'apparition d'un comportement chaotique.

Une conséquence de cela est qu'il est impossible de prendre en compte les interactions entre mâles et femelles avec ces modèles. Aussi, on se contente en général de n'étudier qu'un seul sexe. Dans la grande majorité des cas, il s'agit des femelles. Il y a deux raisons importantes à cela :

• Une raison théorique : les femelles pouvant être définies comme le sexe investissant le plus dans la production d'un nouvel individu donné, elles sont fréquemment en position de sexe limitant : toutes les femelles sont fécondées et c'est leur nombre et leur capacité à produire des individus viables qui limite le nombre de naissances (voir les notions de sexe rare et d'anisogamie en sélection sexuelle). Dans ces conditions ("toutes les femelles sont fécondées, quel que soit le nombre de mâles"), il est clair qu'il est plus intéressant de suivre le nombre de femelles que de mâles.
• Une raison pratique : il est souvent plus simple de déterminer le nombre de descendants d'une femelle que d'un mâle, ce qui rend les contributions des femelles plus faciles à obtenir en pratique.

Un modèle qui ne prend en compte que les femelles est fréquemment qualifié de modèle female-based. La majorité des modèles sont female-based, mais il existe également des modèles no-sex où tous les individus sont pris en compte, indépendamment de leur sexe (pertinent pour les espèces se reproduisant principalement de façon asexuée). Enfin, dans le cas où le sexe mâle serait limitant (par exemple, du fait d'une inversion des sexes) et/ou il serait plus facile de quantifier la descendance d'un mâle, un modèle ne prenant en compte que les mâles serait plus adapté.

Hypothèses et limites

Les modèles matriciels de population reposent sur deux hypothèses fortes qu'il est important d'avoir à l'esprit car elles sont cruciales pour assurer la validité des résultats obtenus :

1. Les interactions entre les individus n'ont pas d'impact spécifique sur la dynamique de la population.
2. Les traits démographiques des individus sont homogènes au sein des classes du modèle et constants au cours du temps.

La première hypothèse permet d'obtenir la linéarité du modèle (A(x n₁ + n₂) = x An₁ + An₂). La seconde justifie des techniques utilisées pour étudier les modèles matriciels, comme l'utilisation de chaînes de Markov.

Ces hypothèses conduisent à certaines conclusions absurdes (comportement asymptotique géométrique, obtention d'individus arbitrairement âgés dans des modèles en classes de taille...) et il est donc important que l'expérimentateur les ait bien à l'esprit à la fois au moment du choix d'un modèle matriciel comme outil de modélisation et au moment de l'interprétation des résultats obtenus.

Même s'il est clair qu'en pratique ces hypothèses ne sont jamais vérifiées exactement, les modèles matriciels restent utiles pour réaliser des prévisions à court terme et pour obtenir des informations sur l'état actuel d'une population.

Exemple : modèle en classes d'âge

Les modèles en classes d'âge, également appelés modèles de Leslie, font partie des modèles les plus fréquemment rencontrés : pour un certain nombre de taxons (notamment un grand nombre de mammifères), les probabilités de survie et les fertilités dépendent en effet principalement de l'âge des individus. Pour des raisons historiques d'une part et du fait du grand nombre de résultats qu'ils permettent d'obtenir d'autre part, ces modèles ont une place centrale dans l'étude des modèles matriciels de populations.

La forme d'un modèle en classes d'âge est contrainte par le fait qu'à chaque pas de temps, les individus n'ont que deux possibilités : survivre (et donc vieillir d'exactement un intervalle de projection), ou mourir (et donc disparaître du modèle). Il est impossible pour un individu de rajeunir, de ne pas vieillir ou de vieillir plus vite que les autres. Ainsi, les seules transitions de survie possibles sont celles allant d'une classe d'âge i à la classe d'âge i + 1. Le coefficient associé à cette transition, noté s_i, correspond à la proportion d'individus d'âge i survivant d'un pas de temps sur l'autre. De même, les nouveau-nés se trouvent forcément dans la première classe d'âge. Les transitions reproductives pointent donc toutes vers la classe 1. Les coefficients associées, notés f_i, correspondent au nombre moyen d'individus produits par un individu de classe i. La forme générale du modèle est donc :

${\displaystyle \mathbf {A} ={\begin{pmatrix}f_{1}&f_{2}&\cdots &f_{m-1}&f_{m}\\s_{1}&0&\cdots &0&0\\0&s_{2}&\cdots &0&0\\\vdots &\vdots &\ddots &\vdots &\vdots \\0&0&\cdots &s_{m-1}&0\end{pmatrix}}}$

La figure 1A est un exemple de graphe du cycle de vie associé à un modèle en trois classes d'âge.

Comme nous l'avons dit, un des intérêts de ce modèle est qu'il permet d'obtenir un grand nombre de formules explicites. Par exemple, le polynôme caractéristique de A permet de retrouver directement l'équation d'Euler-Lotka (en). En effet, ce polynôme est :

${\displaystyle P(X)=\mathrm {det} \left(X\mathbf {I} -\mathbf {A} \right)=X^{m}-\ell _{1}f_{1}X^{m-1}-\ell _{2}f_{2}X^{m-2}-\quad \ldots \quad -\ell _{m-1}f_{m-1}X-\ell _{m}f_{m}}$

où on a noté ℓ₁ = 1 et ℓ_i = s₁...s_i-1 la probabilité qu'un individu survive jusqu'à l'âge i (fonction de survie ou survivorship). Or λ, le taux de croissance asymptotique de la population, est une valeur propre de A (cf section sur le régime asymptotique) donc c'est une racine de P, i.e. P(λ) = 0. Comme λ>0, on peut diviser par λ pour obtenir :

${\displaystyle \sum _{i=1}^{m}\lambda ^{-i}\phi _{i}=1}$

où ϕ_i = ℓ_i f_i = s₁...s_i-1 f_i est appelée fertilité nette.

Remarque : il existe une variante du modèle de Leslie qui est d'usage relativement fréquent. En effet, il arrive qu'on choisisse de ne pas distinguer les individus de plus d'un certain âge. On groupe alors tous ces individus dans une même catégorie pour obtenir le modèle suivant :

${\displaystyle \mathbf {A} ={\begin{pmatrix}f_{1}&f_{2}&\cdots &f_{m-1}&f_{m}\\s_{1}&0&\cdots &0&0\\0&s_{2}&\cdots &0&0\\\vdots &\vdots &\ddots &\vdots &\vdots \\0&0&\cdots &s_{m-1}&s_{m}\end{pmatrix}}}$

Dans ce modèle, la classe m correspond donc à la classe "plus âgé que...", dans laquelle s'accumulent les individus. La plupart des résultats pour le modèle de Leslie classique peuvent être adaptés à ce modèle.

Exemple : modèle en classes de taille

Pour certains organismes (notamment des plantes ou des animaux à croissance indéterminée), les probabilités de survie et les fertilités dépendent essentiellement de la taille des individus. Il est alors naturel d'utiliser cette variable pour construire un modèle matriciel. La principale différence avec les modèles en classes d'âge est alors que les individus ne sont plus "portés" d'une classe du modèle à l'autre par le temps : il devient possible de rester plusieurs années consécutives dans la même classe. En revanche, comme la taille est corrélée à l'âge, on obtient des modèles donc la forme générale reste proche des modèles en classe de taille. Par exemple, on a typiquement des matrices de projection de la forme :

${\displaystyle \mathbf {A} ={\begin{pmatrix}s_{1}+f_{1}&f_{2}&\cdots &f_{m-1}&f_{m}\\g_{1}&s_{2}&\cdots &0&0\\0&g_{2}&\cdots &0&0\\\vdots &\vdots &\ddots &\vdots &\vdots \\0&0&\cdots &g_{m-1}&s_{m}\end{pmatrix}}}$

C'est ce type de modèle qui est représenté par la Figure 1B. Les g_i correspondent ici à des probabilités de croissance tandis que les s_i correspondent à des probabilités de rester dans la même classe d'une année sur l'autre. Bien sûr, il est possible de compliquer le modèle tout en conservant des classes de taille : on peut tout à fait inclure des possibilités de croissance rapide (transitions de la forme i → i + 2 voire i → i + 3, etc) ou de régression (i → i - 1 ; chez des plantes par exemple).

Analyse mathématique du modèle

Régime asymptotique

L'étude du régime asymptotique consiste à étudier le comportement de la population pour des temps très grands. Elle permet de donner une interprétation biologique des éléments propres de la matrice de projection.

Aspect mathématique

La grande majorité des matrices de projection sont primitives, car les cycles de vie utilisés en pratique sont généralement irréductibles (il existe un chemin reliant tout couple de sommets dans le graphe du cycle de vie) et apériodiques (le PGCD de la longueur des cycles du graphe du cycle de vie est égal à 1). Le théorème de Perron-Frobenius permet alors d'affirmer que :

• A admet une valeur propre réelle λ > 0, strictement supérieure en module à toutes les autres. λ est appelée la valeur propre dominante de A.
• Le sous-espace propre à droite associé à λ est de dimension 1. λ admet un vecteur propre à droite w dont les entrées sont strictement positives (w est choisi de telle sorte que la somme de ses entrées vaille 1).
• Le sous-espace propre à gauche associé à λ est de dimension 1. λ admet un vecteur propre à gauche v dont les entrées sont strictement positives (ici, on choisit v de manière que v⋅w = 1. Un autre choix courant est de le choisir tel que v₁ = 1)

Les résultats précédents permettent de montrer que, pour t assez grand,

${\displaystyle \mathbf {n} (t)\sim \mathbf {v\cdot n} (0)\,\lambda ^{t}\,\mathbf {w} }$

(c'est-à-dire ${\displaystyle \forall i,\,n_{i}(t)/{\big (}\mathbf {v\cdot n} (0)\,\lambda ^{t}\,w_{i}{\big )}\to _{t\to +\infty }1}$. Rappelons qu'on a ici choisi v tel que v⋅w = 1). Concrètement, cela signifie que le vecteur population, n, va venir s'aligner avec le vecteur w puis sera dilaté d'un facteur à chaque pas de temps, et ce indépendamment des conditions initiales, qui n'interviennent que dans le facteur v⋅n(0).

Taux de croissance, structure stable et valeurs reproductives

La formule précédente permet de donner une interprétation biologique des éléments propres :

• λ est le taux de croissance asymptotique de la population
• w est la structure stable, c'est-à-dire que w_i correspond à la proportion d'individus dans la classe i lorsque la structure de la population est à l'équilibre.
• v est le vecteur des valeurs reproductives, c'est-à-dire que v_i peut être vu comme le poids (relatif) qu'un individu de classe i a sur la dynamique de la population à long terme (plus v_i est élevé, plus les individus de la classe i seront pris en compte dans v⋅n(0)).

Régime transitoire

À moins que la population initiale ne soit déjà à sa structure stable (c'est-à-dire que n(0) et w ne soient colinéaires), le régime asymptotique est précédé par une période plus ou moins longue appelée régime transitoire durant laquelle la dynamique de la population peut sembler irrégulière. Comme dans le cas du régime asymptotique, le régime transitoire peut être étudié à l'aide des éléments propres de la matrice de projection ; néanmoins, il faut alors prendre en compte tous les éléments propres, et pas seulement les éléments dominants.

Les effets des différentes valeurs propres de A sur le régime transitoires sont additifs. On peut donc les considérer séparément :

• De façon générale, l'effet d'une valeur propre est d'autant plus marqué et prolongé que son module est grand.
• Les valeurs propres réelles positives ont un effet monotone.
• Les valeurs propres réelles négatives engendrent des oscillations de période 2.
• Les valeurs propres complexes engendrent des oscillations dont la période T est liée à leur argument, θ : T = 2 π / θ.

La convergence vers le régime asymptotique sera d'autant plus rapide que la valeur propre dominante est grande par rapport au module des autres valeurs propres. Ainsi, une façons simple de quantifier la vitesse de convergence est de considérer le taux d'amortissement (damping ratio) :

${\displaystyle \zeta ={\frac {\lambda }{|\lambda _{2}|}}}$

où λ₂ est la seconde valeur propre de plus grand module. ζ est donc strictement supérieur à 1. Plus la valeur de ζ est élevée, plus la convergence vers le régime asymptotique est rapide.

Sensibilité aux paramètres

Dans l'étude des modèles matriciels de population, le terme analyse de sensibilité est souvent utilisé de façon un peu incorrecte pour désigner des questions pouvant relever de analyse de sensibilité, de la propagation des incertitudes, ou du contrôle.

Les intérêts de ce genre d'étude sont multiples : par exemple, les mesures n'étant jamais parfaites en pratique, on peut se demander si les incertitudes sur certains paramètres du modèles influenceront plus ou moins les résultats obtenus (cela peut permettre d'identifier les paramètres pour lesquels une grande précision est nécessaire) ; un autre exemple est qu'on peut se demander comment une population va répondre à une perturbation extérieure (chasse, modification de l'habitat, changement climatique...). Une question de ce type peut être traitée en formulant une hypothèse sur la façon dont la perturbation va modifier les entrées de la matrice de projection, puis en étudiant la répercussion de ces modifications sur certains descripteurs biologiques. Il arrive aussi fréquemment qu'on s'intéresse au problème inverse associé, qui consiste à chercher la perturbation à effectuer pour obtenir un effet souhaité (faire augmenter / diminuer la taille d'une population, etc).

Sensibilités

L'idée la plus naturelle pour quantifier l'impact d'une incertitude / perturbation d'un paramètre θ sur un descripteur X est de considérer le rapport ΔX/Δθ. Plus précisément, on étudie la réponse à une perturbation infiniment petite d'un unique paramètre alors que les autres sont maintenus constants, ce qui revient à considérer la sensibilité de X à θ :

${\displaystyle s_{X}(\theta )={\frac {\partial X}{\partial \theta }}}$

Le taux de croissance λ étant probablement le descripteur le plus important d'une population, les sensibilités de λ aux entrées a_ij de la matrice de projection sont très utilisées en pratique — si bien qu'on utilise généralement le terme sensibilités sans plus de précision pour faire référence à ces sensibilités particulières. Celles-ci peuvent être exprimées en fonction des éléments propres dominants[8] :

${\displaystyle s_{\lambda }(a_{ij})={\frac {\partial \lambda }{\partial a_{ij}}}={\frac {v_{i}w_{j}}{\mathbf {vw} }}}$

où v et w sont les vecteurs propres dominants à gauche et à droite, respectivement (qu'ici on n'a pas forcément choisis tels que v⋅w = 1).

Élasticités

Il arrive fréquemment qu'il soit plus pertinent de considérer la réponse relative à une perturbation relative — autrement dit, Δ_%X/Δ_%θ plutôt que ΔX/Δθ. On peut y voir plusieurs avantages : d'une part, cela permet de faciliter la comparaison entre les valeurs obtenues, qui comme on va le voir sont ramenées à une même échelle ; d'autre part, il n'y a généralement pas d'incertitude sur les entrées de la matrice qui valent zéro (car cela traduit une absence de transition plutôt qu'une transition de taux nul. On pourrait parler de "zéros structurels"). Or les sensibilités à des entrées nulles de la matrice ne sont généralement pas nulles (et peuvent même être extrêmement élevées), ce qui n'est pas forcément pertinent selon la question qu'on se pose.

Cette idée de quantifier la réponse relative à une perturbation relative se traduit par l'utilisation des élasticités :

${\displaystyle e_{X}(\theta )={\frac {\theta }{X}}{\frac {\partial X}{\partial \theta }}}$

Comme pour les sensibilités, on utilise fréquemment le terme élasticités sans plus de précision pour désigner les élasticités du taux de croissance aux entrées de la matrice :

${\displaystyle e_{\lambda }(a_{ij})={\frac {a_{ij}}{\lambda }}{\frac {\partial \lambda }{\partial a_{ij}}}={\frac {v_{i}a_{ij}w_{j}}{\lambda \mathbf {vw} }}}$

avec les mêmes notations que précédemment.

Les élasticités possèdent plusieurs propriétés, dont la plus importante est qu'elles sont positives et que leur somme vaut 1, ce qui permet de les interpréter comme des "quantités normalisées" et facilite leur comparaison. Le fait qu'elles somment à 1 se déduit aisément de l'expression précédente, mais peut également être retrouvé à partir de la définition des élasticités et du théorème d'Euler pour les fonctions homogènes : il suffit de remarquer que λ est une fonction positivement homogène de degré 1 des a_ij (c'est-à-dire qu'en notant f : (a₁₁, a₁₂, ... , a_mm) ↦ λ, on a, pour tout c > 0, f(ca₁₁, ... , ca_mm) = cλ) pour obtenir le résultat immédiatement.

Autres descripteurs de la population

L'intérêt des modèles matriciels de population est qu'ils permettent de calculer un très grand nombre de descripteurs biologiques — dont le taux de croissance λ, la structure stable w, le vecteur des valeurs reproductives v, les sensibilités et les élasticités ne sont que des exemples. Parmi les autres descripteurs que permettent de calculer les modèles matriciels de population, citons[9] :

• La distribution des âges dans les classes du modèle.
• L'espérance de vie.
• Le taux net de reproduction.
• Le temps de génération.

Applications

Mise en œuvre

La simplicité des modèles matriciels de population ne doit pas faire perdre de vue que leur utilisation n'est pas triviale. Notamment, leur mise en œuvre nécessite de répondre à un certain nombre de questions.

Un modèle matriciel est-il pertinent ?

C'est la première question à se poser. Comme tous les modèles, les modèles matriciels de population

1. reposent sur certaines hypothèses (voir la section Hypothèses et limites)
2. ne permettent d'obtenir qu'un certain type de résultats

Ils ne sont donc pas adaptés à toutes les situations... C'est pourquoi l'expérimentateur doit commencer par se demander si la situation étudiée est compatible avec les hypothèses des modèles matriciels de populations ("Le choix d'un modèle en temps discret est-il naturel ?" ; "Une structure discrète de la population est-elle adaptée ?" ; "Un modèle déterministe est il adapté ?" ; "Le phénomène étudié risque-t-il d'être fréquence-dépendant / densité-dépendant ?", etc.) mais aussi si les descripteurs calculés à l'aide de modèles matriciels permettront de répondre à la question d'intérêt ("L'indicateur le plus adapté peut-il être calculé avec les modèles matriciels ?" ; "Un indicateur global est-il pertinent, ou est-ce que la variabilité entre individus risque d'être déterminante ?", etc.).

Faut-il baser le modèle sur les femelles ?

La majorité des modèles ne prennent en compte que les femelles, mais rien n'assure que ce choix soit toujours le plus pertinent (voir section Modèles basés sur les femelles).

Quel intervalle de projection choisir ?

Le choix de l'intervalle de projection est une étape importante qui ne devrait pas être négligée. Dans beaucoup de cas, un choix s'imposera en lien avec le cycle de vie de la population étudiée (typiquement, "un an"). Mais il faut veiller à ce qu'un qui semble évident soit bien pertinent. Notamment :

• L'échelle de temps du phénomène qu'on souhaite étudier est elle compatible avec l'intervalle de projection choisi ? Si l'intervalle de projection est trop court, on risque d'obtenir des résultats aberrants. S'il est trop long, on manquera de précision.
• Si l'intervalle de projection est choisi inférieur à un an car la population étudiée a plusieurs périodes de reproduction par an, toutes les périodes de reproductions sont elles bien équivalentes ?
• Dans le cas d'un modèle en classes d'âge, il faut faire attention à ce que l'intervalle de projection soit bien égal au temps passé par les individus dans une classe.
• etc.

Quelles classes choisir ?

C'est probablement la question la plus complexe et la plus importante lors de la construction d'un modèle matriciel. Même si des tendances générales sont observées (les modèles en classes de taille sont généralement plus adaptés pour des organismes à croissance indéterminée comme les plantes ou les poissons, tandis que des modèles en classes d'âge sont souvent mieux adaptés pour des organismes comme les mammifères[10]), il n'existe pas de règle générale.

Enfin, lorsque la variable structurante choisie est continue, il reste à délimiter les classes. Dans le cas d'un modèle en classes d'âge, ce choix est contraint par le fait que la fourchette temporelle couverte par chaque classe doit être égale à l'intervalle de projection. Mais, dans le cas général, il s'agit d'une question complexe, notamment car deux effets s'opposent : les classes ne doivent pas être trop larges de manière à avoir une description fine de la structure de la population et à ce que les traits démographiques soient homogènes au sein d'une classe. Mais elles ne doivent pas non plus être trop fines de manière qu'il soit possible en pratique d'avoir assez de données pour bien estimer les traits démographiques de chaque classe expérimentalement.

Estimation des coefficients de la matrice de projection

Il est rare que les entrées de la matrice de projection soient mesurées de façon directe dans une population (c'est-à-dire en suivant un nombre élevé d'individus de chaque classe pour estimer leur contribution à chacune des autres classes d'un pas de temps sur l'autre). En général, on dispose de données indirectes à partir desquelles il faut estimer les contributions en faisant certaines hypothèses. Par exemple, s'il est difficile de sexer les jeunes individus, il se peut qu'on ne dispose que des fécondités en termes de "nombre total d'individus produits" (au lieu du "nombre de femelles produites") et d'une estimation du sex-ratio dans une partie de la population. Autre exemple : pour une espèce végétale, on ne peut en général pas retrouver la "mère" d'un nouvel individu. Les fertilités doivent alors être estimées, par exemple au moyen d'un nombre moyen de graines produites par individu, d'un taux de germination, etc.

Il faut également être vigilant au moment où les mesures sont effectuées : dans la plupart des cas, elles sont prises soit juste avant la saison de reproduction (pre-breeding census), soit juste après (post-breeding census). Ce timing doit être pris en compte lorsque les contributions sont calculées à partir de données indirectes. Par exemple, dans un modèle pre-breeding, les individus sont âgés d'une année lorsqu'ils sont observés pour la première fois, et donc seuls les individus ayant survécu à leur première année sont pris en compte. Les termes de fertilités correspondent donc au nombre d'individus mis au monde multiplié par la probabilité de survie de ces individus durant la première année de leur vie — tandis que dans le cas d'un modèle post-breeding il s'agit directement du nombre d'individus mis au monde.

À tout cela s'ajoutent les considérations liées aux méthodes utilisées pour compter les individus (ex : capture-marquage-recapture, etc). L'estimation des coefficients de la matrice de transition peut donc se révéler très simple comme très complexe, en fonction des données disponibles en pratique.

Exemples d'applications

Donner des exemples aussi variés que possible d'applications. Par exemple : démographie humaine, conservation, études théoriques. Donner à chaque fois une (ou plus) référence. Privilégier la qualité à la quantité.

Notes et références

1. (en) Harro Bernardelli, « Population Waves », Journal of the Burma Research Society, vol. 31,‎ 1941, p. 1-18
2. (en) E. G. Lewis, « On the Generation and Growth of a Population », The Indian Journal of Statistics, vol. 6,‎ 1942, p. 93-96
3. (en) Patrick H. Leslie, « On the Use of Matrices in Certain Population Mathematics », Biometrika, vol. 33,‎ 1945, p. 183-212
4. (en) Patrick H. Leslie, « Some Further Notes on the Use of Matrices in Population Mathematics », Biometrika, vol. 35,‎ 1948, p. 213-245
5. (en) Leonard Lefkovitch, « The Study of Population Growth in Organisms Grouped by Stages », Biometrics, vol. 21,‎ 1965, p. 1-18
6. (en) Michael B. Usher, « A Matrix Approach to the Management of Renewable Resources, With Special Reference to Selection Forests », Journal of Applied Ecology, vol. 3,‎ 1966, p. 355-367
7. (en) Tomas de-Camino-Beck et Mark A. Lewis, « A New Method for Calculating Net Reproductive Rate from Graph Reduction with Applications to the Control of Invasive Species », Bulletin of Mathematical Biology, vol. 69,‎ 2007, p. 1341-1354
8. (en) Hal Caswell, « A general formula for the sensitivity of population growth rate to changes in life history parameters », Theoretical Population Biology, vol. 14,‎ 1978, p. 215-230
9. (en) Margaret E. Cochran et Stephen Ellner, « Simple methods for calculating age-based life history parameters for stage-structured populations », Ecological Monographs, vol. 62,‎ 1992, p. 345-364
10. (en) Mark Kirkpatrick, « Demographic models based on size, not age, for organisms with indeterminate growth », Ecology,‎ 1984, p. 1874-1884

Voir aussi

Bibliographie

• Pierre Auger, Christophe Lett, Jean-Christophe Poggiale, Modélisation mathématique en écologie, Dunod (2010)
• Nicolas Bacaër, Histoires de mathématiques et de populations, Cassini (2009)
• (en) Hal Caswell, Matrix Population Models : Construction, Analysis and Interpretation, Sinauer, 2001, 2^e éd.

Liens externes

• GT maths-bio 2013 : Modèles matriciels de population : une introduction à l'étude mathématique des modèles matriciels de population.