Lenia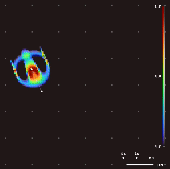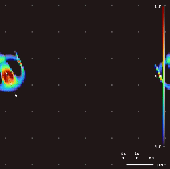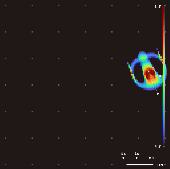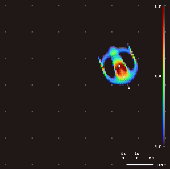

Un exemple de modèle autonome de Lenia.

Une animation montrant le mouvement d'un planeur dans Lenia.

Lenia est une famille d'automates cellulaires créée par Bert Wang-Chak Chan[1],[2],[3]. Lenia a pour objectif d'être un genre de jeu de la vie mais avec un espace, un temps et des états continus (génération continue). En raison de son domaine continu à haute résolution, les modèles autonomes complexes (« formes de vie » ou « vaisseaux spatiaux ») générés dans Lenia sont décrits comme différents de ceux apparaissant dans d'autres automates cellulaires, étant « géométriques, métamériques, flous, résilients, adaptatifs et génériques[1].»

Lenia a remporté le concours de créatures virtuelles 2018 à la conférence sur le calcul génétique et évolutif à Kyoto[4], une mention honorable à l'ALIFE Art Award en 2018 à Tokyo[5], et le prix de la Société internationale pour la vie artificielle (ISAL) pour la meilleure publication de 2019 (dans le domaine de la vie artificielle)[6].

Principes

Illustration des principes de Lenia (voir tableau)

Lenia reprend les principes du jeu de la vie (vie et mort d'une cellule en fonction de son voisinage) mais en essayant de transposer et généraliser les règles du monde discret du jeu de la vie, dans un monde continu.

	Jeu de la vie	Lenia
Etat d'une cellule	0 ou 1 (mort ou vivant)	Nombre continu entre 0 et 1. Le nombre est en général représenté par l'intensité d'une couleur.
Voisinage	8 cellules adjacentes	Zone(s) de convolution en anneau autour de la cellule. (d) ou (e)
Espace	Discret	Continu : les cellules sont aussi petites que l'on veut, le voisinage étant calculé par une zone de convolution.
Règles de vie ou de mort	Nombre de cellules dans le voisinage	Fonction de croissance de la cellule en fonction de la somme des états couverts par le voisinage (valeur de l'état final de la cellule capé à 0 ou à 1) (f) ou (g). Donne un taux de croissance, qui permet de calculer la variation de l'état de ma cellule en fonction du temps.
Temps	Discret	Continu, avec des dt aussi petit que l'on veut, car les règles de vie ou mort donnent des taux de croissance qui permettent de calculer l'état final quel que soit dt. Le temps n'accélère pas en diminuant dt, mais les mouvements deviennent plus fluides.

Motifs

Une partie de la grande variété d'« espèces » de Lenia.

En faisant varier le noyau convolutif, la cartographie de croissance et les conditions initiales, plus de 400 « espèces » ont été découvertes dans Lenia. Ces « espèces » présentent « une auto-organisation, une auto-réparation, des symétries bilatérales et radiales, une dynamique locomotrice et parfois une nature chaotique[7]. Chan a créé une taxonomie pour ces modèles[1].

Travaux connexes

Les automates cellulaires comme réseau neuronal convolutif[8].

D'autres travaux ont noté la forte similitude entre les règles de mise à jour des automates cellulaires et les convolutions. En effet, ces travaux se sont concentrés sur la reproduction d'automates cellulaires à l'aide de réseaux de neurones convolutifs simplifiés. Mordvintsev et al. ont étudié l'émergence de la génération de modèles auto-réparateurs[9]. Gilpin a découvert que n'importe quel automate cellulaire pouvait être représenté comme un réseau neuronal convolutif et a entraîné des réseaux neuronaux pour reproduire des automates cellulaires existants[8]

Dans cette optique, les automates cellulaires peuvent être considérés comme un cas particulier de réseaux neuronaux convolutifs récurrents. La règle de mise à jour de Lenia peut également être considérée comme une convolution à une seule couche (le « champ de potentiel » ${\displaystyle \mathbf {K} }$ ) doté d'une fonction d'activation (la "cartographie de croissance" ${\displaystyle G}$ ). Cependant, Lenia utilise des noyaux fixes beaucoup plus gros et n'utilise pas la descente de gradient.

A voir également

• Le jeu de la vie
• Automate cellulaire
• Morphogenèse

Liens externes

• Le dépôt Github pour Lenia
• Site Web de Chan pour Lenia
• Un séminaire à Stanford donné par Chan
• Lenia, un automate cellulaire continu sur Science étonnante

Notes et références

1. Chan, « Lenia: Biology of Artificial Life », Complex Systems, vol. 28, n^o 3,‎ 15 octobre 2019, p. 251–286 (DOI 10.25088/ComplexSystems.28.3.251, arXiv 1812.05433, lire en ligne)
2. « Lenia », chakazul.github.io (consulté le 12 octobre 2021)
3. (en-US) Siobhan Roberts, « The Lasting Lessons of John Conway’s Game of Life », The New York Times,‎ 28 décembre 2020 (ISSN 0362-4331, lire en ligne, consulté le 13 octobre 2021)
4. « The virtual creatures competition », virtualcreatures.github.io (consulté le 12 octobre 2021)
5. (en-US) « ALife Art Award 2018 », ALIFE Art Award 2018 (consulté le 12 octobre 2021)
6. « 2020 ISAL Awards: Winners »
7. « Lenia », chakazul.github.io (consulté le 13 octobre 2021)
8. (en) Gilpin, « Cellular automata as convolutional neural networks », Physical Review E, vol. 100, n^o 3,‎ 4 septembre 2019, p. 032402 (ISSN 2470-0045, DOI 10.1103/PhysRevE.100.032402, arXiv 1809.02942, lire en ligne)
9. (en) Mordvintsev, Randazzo, Niklasson et Levin, « Growing Neural Cellular Automata », Distill, vol. 5, n^o 2,‎ 11 février 2020, e23 (ISSN 2476-0757, DOI 10.23915/distill.00023, lire en ligne)