|
Inégalité de BonnesenEn mathématiques, l'inégalité de Bonnesen[1],[2] est un raffinement de l'inégalité isopérimétrique dans le plan euclidien. Elle énonce qu'une courbe de Jordan (courbe fermée sans croisement) de longueur englobant une surface d'aire vérifie l'inégalité : où et sont respectivement les rayons d'un plus grand disque inclus dans la surface (de circonférence un cercle inscrit) et du plus petit disque englobant (de circonférence un cercle circonscrit)cette surface . L'inégalité de Bonnesen généralise l'inégalité isopérimétrique car elle implique cette dernière. En effet, d'après l'inégalité de Bonnesen, On retrouve bien l'inégalité isopérimétrique : Le nom de cette inégalité honore Tommy Bonnesen (en) qui fut le premier à établir cette inégalité[3]. DémonstrationLa démonstration présentée ici, due à Hugo Hadwiger[4], montre un résultat un peu plus précis: les deux rayons et sont situés entre les deux racines de la fonction polynomiale du second degré qui à t associe l'aire de la surface où tB est le disque de rayon t centrée en l'origine.
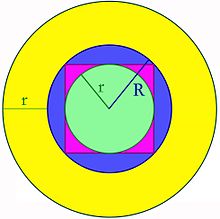 On considère un compact convexe non vide , un cercle inscrit, de rayon et un cercle circonscrit de rayon . Cette situation est illustrée sur la figure de gauche, le compact convexe est le carré violet, le cercle est illustré en bleu et le cercle inscrit en vert. La technique utilisée consiste à considérer la zone bleue Z correspondant aux points de qui ne sont pas dans . La surface Z + rB est doublement mesurée, les symboles rB désignent ici la boule de rayon r et de centre le vecteur nul. Cette figure recouvre intégralement et définit un disque de rayon R + r, illustré en jaune. On en déduit une première égalité :  On découpe alors la surface Z en deux par une droite Δ passant par les centres des deux cercles inscrit et circonscrit. La partie supérieure de Z est notée Zs, comme indiquée sur l'illustration à droite. La somme de Minkowski de Zs et de rB correspond, dans la partie supérieure à la droite Δ, à un demi-disque, de rayon R + r. Si l1 et l2 sont les longueurs des deux intersections de Z avec Δ (voir la figure), l'intersection de la somme avec la partie inférieure à la droite Δ possède une aire égale à πr2 + (l1 + l2)r. On en déduit l'égalité : Il est aussi possible d'évaluer cette aire à l'aide de la formule de Steiner-Minkowski. Comme Zs n'est pas convexe, la formule est une majoration et non pas une égalité : Ici ps désigne la longueur de la partie supérieure de la frontière de S. On peut appliquer exactement le même raisonnement à la partie inférieure à la droite Δ. En utilisant l'indice i pour décrire la partie inférieure, on obtient : En sommant les deux majorations : Le périmètre p de S est en effet la somme de ps et de pi. L'aire de Z est aussi égale à la différence de l'aire d'un disque de rayon R avec l'aire a de S, ce qui donne : La dernière majoration signifie que -r est d'image négative par le polynôme associant à t l'aire de S + tB.
On applique exactement le même raisonnement que le précédent en remplaçant le coefficient r par R, le rayon du cercle circonscrit (R n'est-il pas trop grand pour que cela soit possible ?). On obtient la majoration : ce qui démontre la proposition.
Dire que –r et –R ont une image négative par le polynôme revient à dire que ces valeurs se trouvent entre les racines : Cela signifie aussi que la distance qui sépare R et r est plus petite que le rapport entre le discriminant et π : Références
|


















