Générateur congruentiel linéaire

Un générateur congruentiel linéaire est un générateur de nombres pseudo-aléatoires dont l'algorithme, introduit en 1948 par Derrick Lehmer, sous une forme réduite, pour produire des nombres aléatoires, est basé sur des congruences et une fonction affine.

Définition

Les nombres pseudo aléatoires forment une suite dont chaque terme dépend du précédent, selon la formule :

${\displaystyle X_{n+1}=(a\,X_{n}+c)\mod m}$

où a est le multiplicateur, c l'incrément et m le module.

Le terme initial ${\displaystyle X_{0}~}$ est appelé la graine (seed en anglais). C'est elle qui va permettre de générer une suite apparemment aléatoire. Pour chaque graine, on aura une nouvelle suite. Cependant, il est possible que certaines graines permettent d'obtenir une suite plus aléatoire que d'autres.

Du fait de l'opération mod (reste dans la division euclidienne de ${\displaystyle (a\,X_{n}+c)}$ par m), les termes de cette suite sont compris entre 0 et ${\displaystyle (m-1)}$. De plus, comme chaque terme dépend entièrement du précédent, si un nombre apparaît une deuxième fois, toute la suite se reproduit à partir de ce nombre. Or le nombre de valeurs que le nombre peut prendre étant fini (égal à m), la suite est amenée à se répéter au bout d'un certain temps. On dit qu'elle est ultimement périodique.

Du bon choix des paramètres a, c et m

Dans ce type d'algorithme, la qualité du générateur va entièrement dépendre du choix de a, c et m car on ne peut pas se satisfaire d'un générateur qui produit des suites plus ou moins aléatoires, sans aucune raison apparente, selon le choix de X₀.

Un mauvais exemple

Choisir les valeurs a, c et m « au hasard » n'est pas une bonne idée. Prenons un exemple, soit le générateur congruentiel linéaire employant les valeurs a = 25, c = 16, m = 256, nous obtenons :

• avec X₀ = 125, la suite : 125, 69, 205, 21, 29, 229, 109, 181, 189, 133, 13, 85, 93, 37, 173, 245, 253, 197, 77, 149, ...
• avec X₀ = 96, la suite : 96, 112, 0, 16, 160, 176, 64, 80, 224, 240, 128, 144, 32, 48, 192, 208, 96, 112, 0, 16, ...,
• avec X₀ = 50, la suite : 50, 242, 178, 114, 50, 242, 178, 114, 50, 242, ...
• avec X₀ = 10, la suite : 10, 10, 10, 10, ...

Il est clair que ces suites ne peuvent être considérées comme aléatoires.
On voit donc bien que l'on doit choisir avec précaution les paramètres du générateur si l'on espère obtenir des nombres qui s'approchent de l'aléa parfait. Il faut alors se demander comment choisir a, c et m convenablement.

Choix du module

Les générateurs congruentiels font intervenir un calcul modulo m, et donc a priori une division euclidienne, ce qui peut avoir un coût de calcul important dans le cadre d'une utilisation fréquente du générateur. La solution la plus simple est d'utiliser un module de type m = 2^e. En effet, les ordinateurs calculant naturellement en base binaire, un tel choix est tout à fait transparent pour eux, ce qui rend inutile une division euclidienne.

Toutefois, ce choix présente une limite importante : les bits dits de poids faible (les bits les plus à droite) sont beaucoup moins aléatoires que ceux de la partie de poids fort (les bits les plus à gauche). En effet, si d est un diviseur de m, alors la suite Y_n, telle que :

${\displaystyle Y_{n}=X_{n}\mod d}$

satisfait à la suite congruentielle linéaire :

${\displaystyle Y_{n+1}=(a\cdot Y_{n}+c)\mod d}$

en particulier, avec d = 2^k, pour k fixé, compris entre 1 et e, on voit que les k chiffres de poids faible, ont une période maximale de 2^k, évidemment inférieure à m.
Pour remédier à ce problème, on peut ne garder que les bits de poids fort, c'est-à-dire garder les bits les plus à gauche du nombre obtenu. Si l'on tronque les k derniers bits, on aura alors un générateur pseudo aléatoire de nombres compris entre 0 et ${\displaystyle 2^{e-k}-1}$.

Une autre solution consiste à prendre un module du type ${\displaystyle m=2^{e}\pm 1}$, ce qui permet encore d'éviter une division euclidienne par une astuce (cf. The Art Of Computer Programming de D. E. Knuth).

Choix du multiplicateur et de l'incrément

Afin de pouvoir choisir une graine ${\displaystyle X_{0}}$ sans contraintes entre ${\displaystyle 0}$ et ${\displaystyle m-1}$, il faut chercher à maximiser la période du générateur. Or il se trouve que les valeurs de ${\displaystyle a}$ et ${\displaystyle c}$ sont connues, ce qui permet d'obtenir une période maximale (égale à ${\displaystyle m}$).

Si ${\displaystyle c\not =0}$ la période d’un générateur congruentiel linéaire est maximale si et seulement si :

1. ${\displaystyle c}$ est premier avec ${\displaystyle m}$. ${\displaystyle pgcd(c,m)=1}$.
2. Pour chaque nombre premier ${\displaystyle p}$ divisant ${\displaystyle m}$, ${\displaystyle (a-1)}$ est un multiple de ${\displaystyle p}$.
3. ${\displaystyle (a-1)}$ est un multiple de 4 si ${\displaystyle m}$ en est un.

On remarquera que l'on possède un théorème d'équivalence (si et seulement si) : la période est maximale pour toutes les valeurs qui possèdent les propriétés du théorème et seulement pour celles-là.

On possède, de plus, de conditions suffisantes dans le cas particulier où c est nul. Ainsi, pour c nul la période d'un générateur congruentiel linéaire est maximale si^[citation nécessaire] :

1. ${\displaystyle m}$ est premier.
2. ${\displaystyle a^{m-1}-1}$ est un multiple de ${\displaystyle m}$.
3. ${\displaystyle a^{j}-1}$ n'est pas divisible par ${\displaystyle m}$, pour ${\displaystyle j=1,...,m-2}$

Attention: ce n'est pas une équivalence !

Le potentiel

Le potentiel est une notion qui permet d'écarter certains générateurs insuffisamment aléatoires. Il est toujours défini que pour une suite possédant une période maximale (et ce, d'après la deuxième propriété énoncée plus haut). On ne peut pas toujours le définir sur les autres générateurs, et il existe de bons générateurs sur lesquels le potentiel n'est pas défini.

Le potentiel ${\displaystyle s}$ d’une suite possédant une période maximale est défini comme le plus petit entier tel que :

${\displaystyle (a-1)^{s}\equiv 0\mod m}$

Pour une suite de période maximale, on peut prendre ${\displaystyle X_{0}=0}$, et donc :

${\displaystyle X_{n}={\frac {a^{n}-1}{a-1}}\cdot c\mod m}$

ainsi, avec ${\displaystyle a^{n}=((a-1)+1)^{n}}$:

${\displaystyle X_{n}=c\cdot \left(n+{n \choose 2}\cdot (a-1)+\ldots +{n \choose s}\cdot (a-1)^{s-1}\right)\mod m}$

et un potentiel inférieur ou égal à trois, apparaît immédiatement comme trop faible car la suite n’est pas suffisamment aléatoire. En fait un potentiel de 5 ou plus est conseillé.

Rappelons cependant que la notion de potentiel est uniquement là pour écarter quelques mauvais générateurs. Un générateur possédant un potentiel supérieur à 5 ne peut en aucun cas être d’emblée considéré comme bon, il doit d’abord subir quelques tests.

Tests statistiques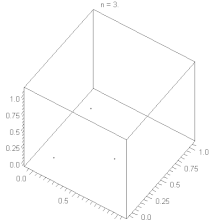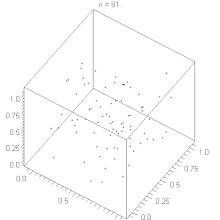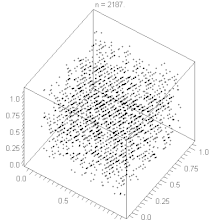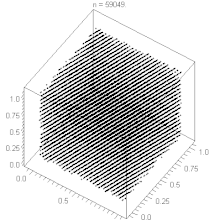

Générateur congruentiel linéaire en 3D

Comme tous les générateurs de nombres pseudo-aléatoires, le générateur congruentiel linéaire doit être soumis à une série de tests avant d’être homologué.

Le plus connu d’entre eux, le test de fréquence n'est généralement pas un problème pour un générateur congruentiel linéaire de période maximale, mais il existe bien d'autres tests : Test des séries, Gap test, Run test, ... ;
l'un des plus discriminant, car aucun générateur congruentiel linéaire démontré mauvais ne l’a réussi, est le Test spectral.

Exemples

Algorithme	a	c	m	Remarques
RANDU	65539	0	2^31	Biaisé et fortement déconseillé
générateur de Robert Sedgewick	31415821	1	10^8	Intéressant mais déconseillé (essayer avec ${\displaystyle X_{0}=0~}$)
Standard minimal	16807	0	2^31-1

• RANDU défini par ${\displaystyle X_{n+1}=65539X_{n}\mod 2^{31}}$. Implanté sur les IBM System/370 et réputé mauvais par tous ceux qui ont à l'utiliser sérieusement^[réf. souhaitée].
• Le générateur de Turbo Pascal défini par ${\displaystyle X_{n+1}=(129X_{n}[phone])\mod 2^{32}}$. On sait dans 1 cas sur 129 que ${\displaystyle X_{n+1}>X_{n}}$, ce qui est un biais énorme pour une application scientifique. En plus comme 129 est de la forme 2^n + 1, les nombres produits ne sont pas si « aléatoires que ça » [cf. Knuth p.23].
• Le générateur d'UNIX (dont le comité ANSI C a heureusement recommandé de ne conserver que les 16 bits de poids fort) :

${\displaystyle X_{n+1}=(1103515245X_{n}+12345)\mod 2^{31}}$. Même la documentation du Berkeley 4.2 admet que les bits de poids faible des nombres produits ne sont pas vraiment aléatoires.

Autres exemples

Knuth recense dans « Seminumerical Algorithms » un certain nombre de générateurs congruentiels linéaires de qualité. S'il n'est pas possible d'utiliser le Standard Minimal, on pourra essayer par exemple :

• ${\displaystyle X_{n+1}=(137X_{n}+187)\mod 2^{8}}$ (une suite cyclique de 256 nombres, est-ce encore du hasard ?)
• ${\displaystyle X_{n+1}=(1664525X_{n}[phone])\mod 2^{32}}$ : générateur de Knuth & Lewis
• ${\displaystyle X_{n+1}=69069X_{n}\mod 2^{32}}$ : générateur de Marsaglia au multiplicande remarquable, utilisé sur le VAX
• ${\displaystyle X_{n+1}=31167285X_{n}\mod 2^{48}}$ : générateur de Lavaux & Jenssens
• ${\displaystyle X_{n+1}=6364136223846793005X_{n}\mod 2^{64}}$ : générateur de Haynes

Dans tous ces cas, comme le modulant est une puissance de 2, les bits de poids faible des nombres produits ne sont pas eux très « aléatoires ». Il est par conséquent préférable de ne conserver que les poids forts (16 bits par exemple), comme le fait le générateur de Borland C++ par exemple :

• ${\displaystyle X_{n+1}=(22695477X_{n}+1){\bmod {2}}^{32}}$ et on sort ${\displaystyle (X_{n+1}\gg 16){\bmod {2}}^{15}}$

Ce faisant, la période du générateur reste la même mais on ne va produire que des nombres compris entre 0 et 65535, chacun se retrouvant 32768 fois dans la suite.

Un autre exemple serait de mixer la sortie d'un générateur congruentiel linéaire et d'un registre à décalage à rétroaction linéaire[1].

Références

1. (en) « Alexpukall/prng64 : pukall prng 64 : mix the output of an lfsr 64 and an lcg 64 (c language or 6502 assembly) », sur GitHub (consulté le 12 novembre 2023).

Voir aussi

Bibliographie

(en) Donald E. Knuth, The Art of Computer Programming, vol. 2 : Seminumerical Algorithms, 3^e éd., Addison-Wesley, Boston, 1998

Articles connexes

• Générateur de nombres aléatoires
• Générateur de Lehmer (en)