Crise de traînée

La crise de traînée d'un corps (3D ou 2D[n 1]) est un phénomène très contre intuitif où, alors que la vitesse de l'écoulement augmente, le coefficient de traînée ${\displaystyle C_{x}}$ du corps (et même éventuellement sa traînée) diminue(nt) drastiquement. Cette crise peut être représentée par une courbe du ${\displaystyle C_{x}}$ selon le Reynolds de l'écoulement. Elle est due au changement de l'écoulement sur le corps occasionné par la transition de sa couche limite depuis l'état laminaire jusqu'à l'état turbulent.

Si cette crise de traînée a été découverte en premier pour la sphère, elle existe également pour le cylindre présenté en travers d'un écoulement ainsi que, d'une façon générale, pour tous les corps suffisamment profilés 2D et 3D[n 1].

Histoire

La crise de traînée de la sphère semble avoir été constatée en premier par l'étudiant russe G.I.Lukyanov[n 2] qui expérimentait dans la soufflerie de l'Université de Moscou. Son enseignant, Nikolaï Joukovski conjectura très correctement que ce paradoxe pouvait être expliqué par le « décollement des lignes de courants à différents points de la sphère à des vitesses différentes ».

En Europe, il semble que la même crise de traînée ait été constatée (au moins qualitativement) par Giulio Costanzi de la Brigada Specialisti, à Rome[n 3],[1].

Traînées (en grammes-force !) de trois sphères selon leur vitesse telle que mesurées par les collaborateurs d'Eiffel

En France, c'est en 1912 que les collaborateurs d'Eiffel, en mesurant la Traînée de sphères de différents diamètres constatent que cette traînée diminue dans une certaine plage de vitesse (alors que cette vitesse augmente, image ci-contre).

L'ingénieur principal de la soufflerie fait état de ce problème dans un courrier à Eiffel. Celui-ci lui répond :

« Le 13 août 1912. Mon cher Mr Rith, J'ai reçu votre lettre du 12. Les résultats pour la sphère de 24,4 avec les vitesses de 4 à 8 m sont plus que bizarres et des expériences aussi discordantes ne peuvent être bonnes[2]. Elles ont besoin d'être refaites. Achetez une nouvelle sphère de 15 à 18 cm[3]. »

C'était la première fois, depuis qu'Eiffel et ses collaborateurs faisaient des mesures dans leur soufflerie, que la traînée d'un corps simple leur apparaissait aussi nettement comme n'étant pas simplement liée au carré de la vitesse, bien que plusieurs de leur mesures leur aient montré que ce phénomène pouvait exister à cause de la friction sur les corps fusiformes[4]. À la lecture de ce courrier d'Eiffel à Rith, on est replongé dans le moment historique de la découverte de la crise de traînée de la sphère.

Coefficient de traîné K des trois sphères d'Eiffel

Voici (ci-contre) le graphe rassemblant les courbes des coefficients de traînée des trois sphères en fonction de notre moderne Nombre de Reynolds :

Les trois courbes ne se chevauchent pas (comme elles le font dans les mesures modernes), mais la crise de traînée se développe bien au même Reynolds.

Cette découverte de la crise de traînée des sphères fut d'ailleurs considérée, au départ comme erronée : Eiffel écrit dans sa note sur la résistance des sphères dans l'air en mouvement, note qui est présentée à l'Académie des Sciences dans sa séance du 30 décembre 1912 : « Le principal laboratoire aérodynamique allemand, celui de Göttingen, a attribué à ce coefficient une valeur deux fois et demie plus forte [que celui qu’Eiffel avait trouvé à son laboratoire du Champ de Mars]. Il a, du reste, publié que celui que j'avais donné moi-même était une erreur manifeste de ma part et ne pouvait qu'être le résultat d'une faute de calcul. »

Dispositif de mesure de la traînée de la sphère par son recul dans la soufflerie d'Eiffel

Dans sa Note à l'Académie des Sciences, Eiffel écrit : « J’ai vérifié ces diverses conclusions en suspendant les sphères par des fils très fins et en observant leur déplacement par rapport à la verticale au moyen d’une lunette spéciale. On peut se rendre compte de ces anomalies et constater qu’il existe bien deux régimes d’écoulement, en examinant la marche des filets [d’air] autour de la sphère à l’aide d’un fil léger porté par une tige très mince. Au-dessous de la vitesse critique, il se forme à l’arrière [de la sphère] un cône de dépressions, d’une longueur presque égale au diamètre de la sphère, et analogue à celui qui se produit à l’arrière des plaques frappées normalement par le vent. Au-dessus de cette vitesse critique, existe le nouveau régime pour lequel ce cône a disparu et se trouve remplacé par une région où l’air n’est relativement pas troublé. »

En 1914, dans Nouvelles recherches sur la résistance de l'air et l'aviation faites au laboratoire d'Auteuil, p 89, Eiffel revient d’ailleurs sur cette question : « Lord Rayleigh, l'éminent directeur du National Physical Laboratory, a adressé une note à l'Académie des Sciences (C. R. de l'Académie des Sciences du 13 janvier 1913) dans laquelle il a fait remarquer que les produits vd de la vitesse critique par le diamètre de la sphère sont à peu près constants. » D’après Pierre Rebuffet[5], cette remarque de Rayleigh « est, sans doute, la première application du concept de Reynolds ».

Notons que dans les pays anglophones, la crise de traînée de la sphère est souvent nommée « Eiffel paradox » (voir Drag crisis).

Cas du cylindre infini présenté en travers d'un écoulement

Comparaison des ${\displaystyle C_{x}}$ de la sphère et du cylindre

Comme la sphère, le cylindre infini présenté en travers de l'écoulement connaît une crise de traînée. Le Reynolds auquel se produit cette crise du cylindre (Reynolds critique) est approximativement le même que celui à laquelle la sphère vit sa propre crise.

Cette crise de traînée du cylindre fut également étudiée par Eiffel[n 4].

La crise de ${\displaystyle C_{x}}$ correspond également à une crise du Strouhal (c'est une façon très nette de la repérer). Comme ils le font pour la sphère, les ingénieurs attribuent donc au cylindre deux ${\displaystyle C_{x}}$ : le ${\displaystyle C_{x}}$ sous-critique (autour de 1,2) et le ${\displaystyle C_{x}}$ supercritique (autour de 0,2).

Mesures et représentations

La courbe rouge (courbe « standard ») dessine le ${\displaystyle C_{x}}$ de la sphère d'après dix régressions analytiques établies par Clift, Grace et Weber.

Depuis l'époque héroïque des premiers « souffleurs »[n 5], les chercheurs n'ont eu de cesse que d'affiner leurs mesures du ${\displaystyle C_{x}}$ de la sphère dans toute la plage des Reynolds possibles. Ces mesures sont rendues difficiles par la difficulté de contention des sphères (la présence d'un dard de contention, à l'aval de ces sphères, suffit à modifier significativement l'écoulement)[n 6].

Clift, Grace et Weber[6] ont établi une courbe « standard » du ${\displaystyle C_{x}}$ de la sphère sur toute la plage de Reynolds possibles ; cette courbe est composée de dix régressions mathématiques simples (courbe rouge du graphe ci-contre].

Bien sûr le ${\displaystyle C_{x}}$ de la sphère, en plus d'être dépendant du Reynolds, l'est aussi de la turbulence de l'écoulement (considérée comme nulle pour la courbe rouge de ce graphe) et de la rugosité de la sphère (c'est ce qui explique, par exemple, les courbes de ce graphe consacrées aux balles de sport - golf, tennis ou foot - qui sont plus ou moins rugeuses).

Dans un écoulement non turbulent, par contre, on considère généralement que le Reynolds critique[n 7] de la sphère se situe autour de 350 000. La turbulence de l'écoulement, ainsi que la rugosité de la sphère, anticipent la crise de traînée (c.-à-d. font que cette crise se produit à un Reynolds plus faible). Les ingénieurs attribuent à la sphère lisse deux ${\displaystyle C_{x}}$, le ${\displaystyle C_{x}}$ sous-critique (0,5) et le ${\displaystyle C_{x}}$ supercritique (autour de 0,07). Après le petit plateau supercritique, la courbe du ${\displaystyle C_{x}}$ présente une remontée (c'est ce que l'on appelle le régime « transcritique »[n 8] ou « hypercritique », mais les Reynolds correspondant à ce dernier régime sont souvent en dehors des Reynolds pouvant être atteints dans la vie courante.

La crise de traînée des corps 2D et 3D

${\displaystyle C_{x}}$ alaire de profils symétriques à incidence nulle selon leur Reynolds et leur épaisseur.

Les crises de traînée de la sphère et du cylindre sont les archétypes des crises de traînée des corps 3D et 2D[n 1]. Tous les corps suffisamment profilés[n 9] connaissent une crise de traînée (image ci-contre).

Pendant la première guerre mondiale, Max. M. Munk, un collaborateur de L. Prandtl[n 10] fut chargé de rédiger un rapport sur le problème de cette crise de traînée pour les entretoises (ou mâts) et les câbles qui fleurissaient entre les ailes des biplans et triplans de l’époque. Munk expliqua dans son rapport de juin 1917 : « En particulier, une réduction de vitesse (par exemple lorsqu’un avion passe d’une vitesse en palier horizontal à une vitesse plus faible de montée) peut résulter en une soudaine augmentation de son coefficient de traînée et souvent même en une augmentation considérable de la traînée elle-même[7],[8]. »

Le graphe ci-contre dessine la crise de traînée de profils symétriques de différentes épaisseurs selon le Reynolds longitudinal de leur écoulement (à incidence nulle)[9],[10]. La crise de traînée du cylindre figure sur ce graphe, comme celle du cylindre de section elliptique présenté selon sa plus forte épaisseur.

On note sur ce graphe que les profils de 12 % d'épaisseur relative (épaisseur courante en aviation), par exemple, suscitent une traînée très importante à bas Reynolds : c'est pourquoi il convient d'utiliser des profils spéciaux pour les vols à bas Reynolds (modèles réduits d'avion, drones, avions à propulsion humaine).

Cependant, dans Résumé des travaux exécutés pendant la guerre au laboratoire aérodynamique Eiffel, Gustave Eiffel fait remarquer qu’il « n’y a pas lieu pour les fils et les câbles non fuselés d’envisager [la crise de traînée]. » Ce qui signifie que ces corps présentent un Reynolds trop faible pour qu'ils puissent connaître une crise de traînée (avec passage en régime supercritique) ; en effet, pour un câble de 6 mm de diamètre, cette crise n’arriverait qu’à 500 m/s, soit au-dessus de la vitesse du son.

De la même façon que ces corps 2D, les corps 3D (tels que, par exemple, les dirigeables et les carénages de roues en aviation légère) font montre de la même crise de traînée aux faibles Reynolds.

Explication physique dans le cas d'une sphère

La crise de traînée de la sphère est l’archétype des crises de traînée se produisant avec des corps suffisamment profilés (corps 3D comme les ellipsoïdes ou les corps de moindre traînée, et corps 2D comme le cylindre, les haubans profilés ou les profils d’ailes).

Animation montrant les deux régimes de la sphère

La principale explication de la brusque diminution du ${\displaystyle C_{x}}$ de la sphère lors de l’augmentation du Reynolds fut génialement proposée par Ludwig Prandtl en 1927[11]. Ce pas de géant de Prandtl ouvrait l’espace tout entier (l’atmosphère, les océans, etc.) au nombre adimensionnel découvert quelques décennies auparavant par Osborne Reynolds dans les écoulements confinés à l’intérieur des tuyaux. Voici cette explication de L. Prandtl :

La crise de trainée est due à la transition de la couche limite existant à la surface de cette sphère depuis un régime laminaire jusqu’à un régime turbulent.

Trois régimes de la sphères (régime non-visqueux et régimes sous-critique et supercritique.

Considérons la sphère en régime sous-critique (ou « premier régime ») : Dans ce régime, le décollement de l’écoulement se produit à un angle au centre depuis le point d’arrêt de ~82°. Comme à cet angle de ~82° la couche limite sur la sphère est dans l’état laminaire, on nomme parfois ce décollement sous-critique « décollement laminaire »[12].

Or plus le Reynolds de l’écoulement croît et plus la transition de la couche limite (depuis le régime laminaire jusqu’au régime turbulent) se produit près du point d’arrêt ; en conséquence, à un certain Reynolds, la transition de la couche limite va se produire avant les ~82° où se produit le décollement en régime sous-critique (décollement laminaire). La couche limite va donc devenir turbulente avant ces ~82°.

Mais une qualité notable de la couche limite turbulente est qu’elle résiste beaucoup mieux au décollement que la couche limite laminaire : le décollement va donc reculer jusqu’à un angle de ~120°, ce qui place la sphère dans le régime supercritique (ou second régime).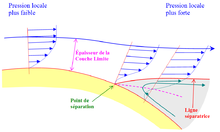

Schéma montrant le décollement de la couche limite sous l’influence de la pression en provenance de l’aval.

D'une façon générale, le décollement de l'écoulement sur un corps est dû à la pénétration, dans la couche limite, de la surpression venant de l’aval (schéma ci-contre). Or le profil des vitesses existant dans la couche limite turbulente est « plus plein » et plus énergétique que le profil des vitesses dans la couche limite laminaire. De ce fait la couche limite turbulente résiste mieux à la pénétration de la surpression en provenance de l’aval et donc au décollement.

En simplifiant beaucoup, tout se passe comme si la couche limite turbulente était plus visqueuse ou collante que la couche limite laminaire : le décollement de l’écoulement en est repoussé vers l’arrière.

Conscient qu'il était difficile de croire qu'une diminution de traînée puisse être obtenue par un passage de la couche limite à l'état turbulent (l'écoulement laminaire étant souvent considéré comme un écoulement produisant moins de traînée), Prandtl conçut l'expérience, maintenant célèbre, où la transition de la couche limite est provoquée par l'usage d'un fil turbulateur placé sur l'hémisphère avant de la sphère : ce fil déclenchant la transition de la couche limite jusqu'à l'état turbulent, le ${\displaystyle C_{x}}$ de la sphère se montre notablement diminué.

Un autre phénomène (autre que la transition de la couche limite) entre en jeu dans la diminution de ${\displaystyle C_{x}}$ consécutive à la crise de traînée de la sphère : cet autre phénomène est la meilleure recompression de la zone d’eau morte (ou de recirculation) existant à l’aval de la sphère (zone grisée sur le schéma ci-contre). Dans le régime sous-critique de la sphère, le coefficient de pression moyen régnant dans cette zone d’eau morte est proche de -0,3. Dans le régime supercritique, le coefficient de pression moyen régnant dans la zone d’eau morte (fortement réduite) est positif et tourne autour de +0,3.

En conséquence, la recompression à l’aval de la sphère est bien meilleure[n 11] : On peut alors noter qu’en supercritique la zone d’eau morte pousse la sphère en avant (alors qu’en sous-critique elle aspire la sphère vers l’arrière) (ceci indépendamment de l’intégration de la distribution de pression sur les autres parties de la sphère).

Définition du Reynolds critique

Dispositif de remorquage de sphère sous autogire pour détermination du Reynolds critique, NACA Report N° 558

Il existe plusieurs définitions du Reynolds critique, Reynolds qui caractérise le passage entre le régime sous-critique et le régime supercritique de la sphère : La définition usuelle est celle utilisée par le NACA ; c’est le Reynolds où les ${\displaystyle C_{x}}$ de la sphère vaut 0,3 (cette valeur étant située à peu près au milieu entre la valeur 0,5 du premier régime et la valeur 0,07 du second régime). Une autre définition est celle utilisée par Hoerner[13] : C’est le Reynolds où le coefficient de pression de culot ${\displaystyle C_{pq}}$ est nul[n 12] ; en effet ce ${\displaystyle C_{pq}}$ passe de ~-0,3 à ~+0,3 au changement de régime.

Ces définitions donnent des Reynolds critiques assez peu différents.

Notes

1. On appelle par simplification corps 2D les corps donnant lieu à un écoulement 2D (en général des cylindres ou des prismes autour duquel l'écoulement se produit dans des plans perpendiculaires au grand axe du corps, l'écoulement dans ces plans étant toujours identique). Par opposition à ces corps 2D, on appelle corps 3D les corps autour duquel l'écoulement se développe dans toutes les directions de l'espace.
2. Une table des coefficients de traînée relevés par Lukyanov peut être trouvée p.73 de N.Ye. Zhukovsky, Collected works of N.Ye.Zukovskii, 1938 (lire en ligne)
3. Eiffel écrivait dans NOUVELLES RECHERCHES SUR LA RÉSISTANCE DE L'AIR ET L'AVIATION FAITES AU LABORATOIRE D'AUTEUIL [1] : « Nous ferons remarquer que le capitaine Costanzi, de la Brigada Specialisti, à Rome, a constaté la même diminution brusque de K [le coefficient de traînée de l'époque] avec des sphères immergées dans l'eau.»
4. Voir cette image, où Eiffel commence à utiliser le produit VD qui est un prototype du Reynolds, à fluide donné
5. Ainsi appelle-t-on les ingénieurs qui pratiquent les mesures dans les souffleries
6. Les soufflerie où les corps sont maintenus par lévitation magnétique commencent à donner leurs résultats
7. Le Reynolds critique admet plusieurs définition (voir le paragraphe sur ce sujet), mais on peut le prendre comme situé à la moitié de la brusque chute du ${\displaystyle C_{x}}$ occasionnée par la crise
8. Dans l'adjectif "transcritique" le préfixe "trans" a le même sens que dans l'adjectif "transneptunien" (qui signifie "au-delà de Neptune) : "transcritique" signifie donc "au-delà de la plage supercritique". Cependant, l'influence du préfixe "trans" de "transatlantique" fait glisser le sens de "transcritique" vers "à l'intérieur de la phase critique" ; c'est pourquoi on peut lui préférer "hypercritique" ou "postcritique".
9. Il n'y a guère que les corps non profilés (comme le disque, la palette infinie présentés frontalement à l'écoulement, etc.) qui ne développent pas de crise de traînée (en conséquence leur ${\displaystyle C_{x}}$ est le même à tous les Reynolds).
10. Max M. Munk émigra en 1921 vers les États-unis pour travailler à la NACA. Il y conçu en 1921 la fameuse Soufflerie à Densité Variable.
11. sans que le ${\displaystyle C_{p}}$ atteigne la valeur unitaire prévue par la théorie en régime non-visqueux.
12. C'est-à-dire que la pression au culot de la sphère vaut la pression atmosphérique ambiante.

Références

1. (en) Rapport NACA, STANDARDIZATION AND AERODYNAMICS, NACA Technical Note N° 134, 1923
2. En fait Eiffel se trompe : L'évolution des traînées dans cette plage de vitesses est bien quadratique (courbe rouge ajoutée au graphe), ce qui siginifie que dans cette plage (exactement entre 4 et 7 m/s) le ${\displaystyle C_{x}}$ est constant. La crise intervient juste après cette plage de vitesse.
3. Source : Aérodynamique Eiffel, archives de la soufflerie d'Auteuil
4. À cette époque, la loi du carré de la vitesse, prévue par Isaac Newton, n'était pas encore fermement établie et beaucoup de comptes-rendus de la soufflerie d'Eiffel commençaient par la phrase « Nous avons trouvé une résistance très sensiblement proportionnelle au carré de la vitesse. »
5. AÉRODYNAMIQUE EXPÉRIMENTALE, par Pierre REBUFFET, 1962, Librairie Polytechnique Ch. Béranger, PARIS, ouvrage essentiel, non réédité
6. (en) BUBBLES, DROPS, AND PARTICLES, BUBBLES, DROPS, AND PARTICLES, 1978
7. …une augmentation de la force de traînée alors que la vitesse est plus faible !
8. Prandtl and the Göttingen school, Eberhard Bodenschatz and Michael Eckert [2]
9. S. F. Hoerner, Résistance à l'avancement dans les fluides, Gauthier-Villars éditeurs Paris Gauthier-Villars éditeurs, Paris
10. (en) S. F. Hoerner, FLUID-DYNAMIC DRAG [3]
11. (en) Ludwig Prandtl, NACA Technical Memorendum No. 452 : MOTION OF FLUIDS WITH VERY LITTLE VISCOSITY [« Über Flüssigkeitsbewegung bei sehr kleiner Reibung »], NACA, 1927 (lire en ligne)
12. L'AÉRODYNAMIQUE ET L'ORIGINE DES TRAINÉES PARASITES, Ewald HUNSINGER - Michaël OFFERLIN [4], Inter.action, 1997
13. TESTS OF SPHERES WITH REFERENCE TO REYNOLDS NUMBER, TURBULENCE AND SURFACE ROUGHNESS, NACA Technical memorendum n° 777, by S. Hoerner https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19930094640.pdf