Courbe quintique

En mathématiques une courbe quintique est une courbe algébrique plane de degré 5. Elle peut être définie par un polynôme de la forme :

${\displaystyle Ax^{5}+By^{5}+Cx^{4}y+Dxy^{4}+Ex^{3}y^{2}+Fx^{2}y^{3}+Gx^{4}+Hy^{4}+Ix^{3}y+Jxy^{3}+Kx^{2}y^{2}+Lx^{3}+My^{3}+Nx^{2}y+Oxy^{2}+Px^{2}+Qy^{2}+Rxy+Sx+Ty+U=0}$

dont les coefficients sont dans un corps commutatif donné. L'équation a 21 coefficients, mais la courbe ne change pas si on les multiplie tous par une constante non nulle. On peut donc fixer U à 1 et se contenter de 20 coefficients. Il y a donc une infinité de quintiques, et chacune d'elles est identifiée par son passage par 20 points génériques.

Une courbe quintique à 28 bitangentes

Caractéristiques

Une courbe quintique (n = 5) définie sur le corps des réels et irréductible peut avoir au maximum :

• (n – 1)(n – 2)/2 + 1 = 7 composantes connexes, d'après le théorème de Harnack[1].

Par ailleurs, les formules de Plücker montrent qu'elle peut avoir au plus :

• (n – 1)(n – 2)/2 = 6 points doubles ;
• n(n – 2)(n – 3)(n + 3)/2 = 120 bitangentes, c'est-à-dire de droites qui sont des tangentes à la courbe en 2 points ;
• 3n(n – 2) = 45 points d'inflexion.

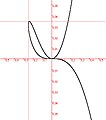
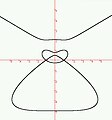
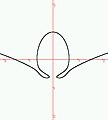
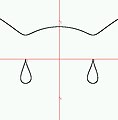
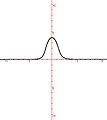
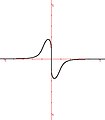
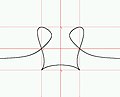
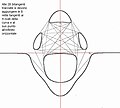
Applications

Les courbes quintiques apparaissent dans l'étude des problèmes de courbes à réaction constante : quelle doit-être la forme de la courbe suivie par un point dans un champ de gravitation de sorte que la réaction du point sur la courbe soit constante ?

Exemples de courbes quintiques définies sur le corps des réels

• Courbe de Burnside

  ${\displaystyle x^{5}-y^{2}-x=0}$

• Courbe kératoïde

  ${\displaystyle x^{5}+x^{2}y-y^{2}=0}$

• Courbe en étrier (it)

  ${\displaystyle y^{2}(y-1)(y-2)(y+5)-(x^{2}-1)^{2}=0}$

• Courbe en quilles

  ${\displaystyle 25x^{5}+45y^{5}+68x^{4}-155y^{4}-12x^{3}+175y^{3}-35x^{2}-65y^{2}+x+4=0}$

• Courbe de l'Hospital

  ${\displaystyle (x^{2}+y^{2})^{2}(y-2)+y(4x^{4}+x^{2}+y^{2})=0}$

• Courbe de Mutasci

  ${\displaystyle x^{4}(x-1)+y^{4}(y-1)-xy=0}$

• Courbe sinusoïdale

  ${\displaystyle x^{5}+y^{5}-x=0}$

• Maracas de Chioppa

  ${\displaystyle 4y^{5}+24x^{4}y+35x^{2}y^{3}-21x^{4}-45x^{2}y^{2}-40y^{3}-46x^{2}y-13y^{2}+57y+36=0}$

• Butterfly Catastrophe

  ${\displaystyle 36864y^{5}+84375x^{4}-24576a^{2}y^{4}+144000ax^{2}y^{2}+4096a^{4}y^{3}-86400a^{3}x^{2}y+13824a^{5}x^{2}=0}$

• Courbe à bulbe

  ${\displaystyle y^{5}+5(x^{4}-y^{4}-1)=0}$

• Feuille de Patarino

  ${\displaystyle x^{2}(13y^{3}-5x^{2}+33y^{2}+36y+14)+y(2x^{4}+5y^{4}+15y^{3}+12y^{2}-10y-16)-5=0}$

• Courbe en tulipe

  ${\displaystyle x^{2}(9x^{2}-8y^{3}+4y^{2}+8)+y(9x^{4}+3y^{4}-7y^{3}+4y^{2}+5y-8)-5=0}$

• Courbe en gouttes

  ${\displaystyle 5y^{5}-x^{4}-2y^{3}+2x^{2}-1=0}$

• Courbe à point triple

  ${\displaystyle x^{5}+y^{5}+xy(x-y)=0}$

• Impulsion unique

  ${\displaystyle y^{5}+100x^{4}y+20x^{2}y^{3}-100x+10y-1000=0}$

• Double impulsion

  ${\displaystyle y^{5}+100x^{4}y+20x^{2}y^{3}+100x=0}$

• Courbe à trois nœuds coulants

  ${\displaystyle (x^{2}-y^{2})(y^{2}-1)(2y-3)-y(x^{2}+y^{2}-2y)^{2}=0}$

• Courbe avec deux points de rebroussement et deux croisements

  ${\displaystyle x^{2}(x^{2}-2)+2y^{2}(y^{3}+y^{2}-1)+2x^{2}y(x^{2}-y^{2}-1)+1=0}$

• Courbe à 36 bitangentes

  ${\displaystyle 20y(x^{2}+y^{2}-1)(5x^{2}+y^{2}-2)+1=0}$

• Courbe avec 10 inflexions

  ${\displaystyle x(xy^{3}-14xy+1)+y(y^{4}+10x^{4}-6y^{2}+4)=0}$

• Courbe à six composantes connexes

  ${\displaystyle (7y^{3}-6x^{2}y-8x^{2}+7y^{2}+4)(10x^{2}+6y^{2}+4y-9)-1=0}$

• Courbe à six croisements

  ${\displaystyle 4x^{2}(3x^{3}+2x^{2}-13x+8)-36y^{2}(y^{3}-2y^{2}-4y+8)+3x^{2}y^{2}(11x-10y+39)-2xy(2x^{3}-18y^{3}+29x^{2}+57y^{2}+59x+3y-90)=0}$

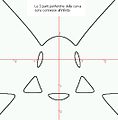
Illustrations

• 
  Courbe de Burnside
• 
  Courbe kératoïde
• 
  Courbe en étrier (it)
• 
  Courbe en quilles
• 
  Courbe de l'Hospital
• 
  Courbe de Mutasci
• 
  Courbe sinusoïdale
• 
  Maracas de Chioppa
• 
  Butterfly Catastrophe
• 
  Courbe à bulbe
• 
  Feuille de Patarino
• 
  Courbe en tulipe
• 
  Courbe en gouttes
• 
  Courbe à point triple
• 
  Impulsion unique
• 
  Double impulsion
• 
  Courbe avec deux points de rebroussement et deux croisements
• 
  Courbe à 36 bitangentes
• 
  Courbe avec 10 inflexions
• 
  Courbe à six composantes connexes
• 
  Courbe à six croisements

Notes et références

(it) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en italien intitulé « Curva quintica » (voir la liste des auteurs).

1. « Topologie des courbes algébriques planes réelles » (consulté le 21 novembre 2018).

Voir aussi

Articles connexes

• Équation quintique
• Courbe quartique
• Courbe algébrique réelle plane

Liens externes

• « Quintique », sur mathcurve.com (site de courbes et surfaces maintenu par Robert Ferreol)
• (en) Eric W. Weisstein, « Quintic Curve », sur MathWorld (brève définition des courbes quintiques)
• (it) « Grafico quintica », sur ascifoni.com (exécutable pour tracer des courbes quintiques)