|
Conjugué isogonalEn géométrie, le conjugué isogonal d'un point dans un triangle est le point où concourent les droites symétriques, par rapport aux bissectrices, des droites passant par chaque sommet et ce point.  Droites antiparallèlesDeux couples de droites (d, d') et (Δ, Δ') sont antiparallèles si les bissectrices des angles qu'ils forment ont même direction[1]. Les angles de droites (d, Δ) et (Δ', d') sont égaux (modulo π). On dit que d' est antiparallèle à d par rapport à (Δ, Δ'). Quatre points A, B, C et D tels que trois d'entre eux ne sont pas alignés sont cocycliques si et seulement si les droites (AB) et (DC) sont antiparallèles par rapport aux droites (AD) et (BC).  Si deux couples de droites (d, d') et (Δ, Δ') sont antiparallèles et concourants, on dit qu'ils sont isogonaux. Lorsqu'une droite est antiparallèle à un côté d'un triangle par rapport aux deux autres, on sous-entend assez souvent les deux derniers côtés. On dira : « dans le triangle ABC, la droite (d) est antiparallèle à (AB) » à la place de « la droite (d) est antiparallèle à (AB) par rapport à (CA) et (CB) ». Droites isogonalesDeux couples de droites concourantes (d, d') et (Δ, Δ') sont isogonaux s'ils sont antiparallèles. Ils ont les mêmes bissectrices. Les angles de droites (d, Δ) et (Δ', d') sont égaux (modulo π). On dit que d' est isogonale à d par rapport à (Δ, Δ'). Soit d, Δ, Δ' trois droites concourantes. La droite d' symétrique de d par rapport à la bissectrice intérieure de Δ et Δ' est isogonale à d par rapport à (Δ, Δ'). Points sur deux droites isogonales Soit (Δ) et (Δ') deux droites concourantes en A, M et N deux points sur deux droites (d) et (d') concourantes en A. Conjugué isogonalTriangle podaireSoit P un point distinct des sommets du triangle ABC et n'appartenant pas au cercle circonscrit, P1, P2, P3 sont les projections orthogonales de P sur les côtés du triangle. Attention aux faux amis français/anglais : le triangle podaire en français se traduit pedal triangle en anglais, qu'il ne faut pas confondre avec le triangle pédal, ou triangle cévien. Point conjugué isogonal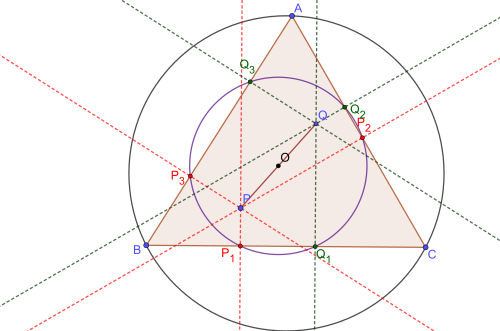 Le conjugué isogonal d'un point P par rapport à un triangle ABC est le point d'intersection des symétriques des droites PA, PB et PC par rapport aux bissectrices des angles du triangle. Ces trois droites symétriques sont concourantes (cela résulte du théorème de Ceva – version trigonométrique). Si P a pour coordonnées barycentriques alors le conjugué isogonal de P a pour coordonnées barycentriques . Toutefois, ce conjugué n'est à distance finie que si, et seulement si, P n'appartient pas au cercle circonscrit du triangle. Si une conique à centre est tangente à chacun des côtés du triangle, ses deux foyers sont des conjugués isogonaux. Les triangles podaires de deux points isogonaux P et Q sont inscrits dans un même cercle de centre le milieu de [PQ]. Cette propriété permet la construction du point isogonal par l'intermédiaire du cercle podaire. Le conjugué isogonal d'un point P n'appartenant pas au cercle circonscrit du triangle (ABC) est aussi le centre du cercle circonscrit du triangle (PaPbPc) construit en prenant les symétriques de P par rapport aux côtés du triangle (ABC)[2].
Autre construction du conjugué isogonal Pour un point P donné dans le plan du triangle △ABC, on considère les images de P par symétrie par rapport aux côtés BC, CA, AB, notés respectivement Pa, Pb, Pc. Alors le centre du cercle circonscrit au triangle PaPbPc est le conjugué isogonal de P. Transformée isogonale d'une droite La transformée isogonale d'une droite par rapport à un triangle ABC est le lieu des conjugués isogonaux des points de cette droite par rapport au triangle ABC. Ce lieu est une conique passant par les sommets du triangle ABC (une hyperbole si la droite passe par l'intérieur du triangle, une ellipse sinon). Exemples particuliers :
Notes et références
Bibliographie
|

