|
Cône de Taylor Un cône de Taylor désigne le cône observé (en électrofilage, électronébulisation et autres processus de pulvérisation hydrodynamique) à partir duquel un jet de particules chargées est émis lors du franchissement d'un seuil de tension. Hormis les processus d'ionisation par électronébuliseur (en spectrométrie de masse), le cône de Taylor est important dans la propulsion à émission de champs (field emission electric propulsion ou FEEP) et les propulseurs colloïdes utilisés avec une haute efficacité (mais une faible puissance) pour la poussée d'engins spatiaux. HistoireLe phénomène est décrit pour la première fois par Sir Geoffrey Ingram Taylor en 1964 avant que l'électrospray ne soit découvert[1]. Ces travaux constituent la continuation de ceux de Zélény[2], qui était parvenu à photographier un cône-jet de glycérine dans un fort champ électrique, et de ceux de Wilson et Taylor (1925)[3], Nolan (1926)[4] et Macky (1931)[5]. Taylor était principalement intéressé par le comportement de gouttes d'eau dans de forts champs électriques, tels que dans les orages. Formation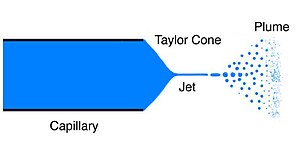 Quand un petit volume de liquide électriquement conducteur est exposé à un champ électrique, la forme du liquide se déforme à partir de sa forme initiale liée à sa tension de surface. Avec l'augmentation de la tension électrique, l'effet du champ électrique devient plus important. Quand le champ électrique commence à exercer une ampleur comparable à la force de la tension de surface sur la goutte de liquide, on observe la formation d'une forme de cône aux côtés convexes et bout arrondi. La forme est proche de celle d'un cône avec un angle total (largeur) de 98,6°[1]. Lorsqu'un certain seuil de tension est atteint le bout légèrement arrondi s'inverse et émet un jet de liquide, phénomène appelé cône-jet (ou cone-jet dans la littérature anglophone), c'est le début du processus d'électronébulisation au cours duquel les ions peuvent être transférés à la phase gazeuse. Il est généralement constaté que, pour parvenir à un cône-jet stable, une tension légèrement supérieure à la tension de seuil est nécessaire. Quand la tension est augmentée plus encore, d'autres modes de désintégration de gouttelettes sont observés. ThéorieSir Geoffrey Ingram Taylor décrit la théorie du phénomène en 1964 en se basant sur des hypothèses générales et énonce que les conditions requises pour former un cône parfait dans de telles conditions nécessitent un demi-angle semi-vertical de 49,3° (angle total de 98,6°) et démontra que la forme de ce cône approchait de la forme théorique précédant la formation d'un jet. Cet angle est connu sous le nom d'angle de Taylor. Cet angle est plus précisément où est le premier zéro de (polynôme de Legendre d'ordre 1/2). Les équations de Taylor reposent sur deux hypothèses: (1) la surface du cône est une surface équipotentielle et (2) le cône existe dans un état d'équilibre. Pour répondre à ces deux critères, le champ électrique doit avoir une symétrie azimutale et avoir une dépendance à la tension de surface pour produire le cône. La solution à ce problème est: où (surface équipotentielle) existe à une valeur de (quel que soit R) produisant un cône équipotentiel. L'angle nécessaire pour pour tout R est une valeur nulle de entre 0 et qui n'existe qu'à 130.7099°. Le complément de cet angle est l'angle de Taylor. Références
|







