|
Atan2
 En trigonométrie, la fonction atan2 à deux arguments est une variante de la fonction arc tangente. Pour tous arguments réels x et y non nuls, est l'angle en radians entre la partie positive de l'axe des abscisses d'un plan, et le point de ce plan de coordonnées (x, y). Cet angle est positif pour les angles dans le sens anti-horaire dit sens trigonométrique (demi-plan supérieur, y > 0) et négatif dans l'autre (demi-plan inférieur, y < 0). La fonction atan2 fut d'abord introduite dans les langages de programmation informatique, mais elle est désormais aussi couramment utilisée dans d'autres domaines de la science et de l'ingénierie. Elle est au moins aussi ancienne que le langage de programmation Fortran et on la trouve maintenant dans la plupart des autres langages. En termes mathématiques, atan2 retourne la détermination principale de la fonction argument appliquée au nombre complexe . Soit . Le résultat pourrait varier de 2π sans aucun impact sur l'angle, mais pour garantir son unicité, on utilise la valeur principale dans l'intervalle ]–π ,π], soit . La fonction atan2 est utilisée dans beaucoup d'applications impliquant des vecteurs de l'espace euclidien, comme pour trouver la direction d'un point à un autre en navigation ou pour effectuer une transformation de coordonnées en astronomie. Une des utilisations principales est la conversion des matrices de rotation en angles d'Euler, pour faire pivoter des représentations graphiques informatiques. Dans certains langages informatiques, l'ordre des paramètres est inversé, ou bien la fonction est dénommée différemment. Sur les calculatrices scientifiques, le résultat de la fonction est souvent issu de la conversion des coordonnées rectangulaires (x, y) en coordonnées polaires. MotivationLa fonction arc tangente à un seul argument ne fait pas la différence entre des directions diamétralement opposées[1]. Par exemple, l'angle anti-horaire à partir de l'axe des x jusqu'au vecteur (1, 1), calculé de la façon habituelle comme arctan(1/1), donne π/4 (radians), ou 45°. De la même façon, l'angle entre l'axe des x jusqu'au vecteur (-1, -1), avec la même méthode arctan(-1/-1), donne encore π/4, alors que la réponse clairement attendue serait plutôt −3π/4, ou −135°. La fonction "atan2" prend en compte le signe des deux composantes du vecteur, et place l'angle dans le bon quadrant. Ainsi, et . De plus, la méthode habituelle ne fonctionne pas dans le cas d'un angle de ± π/2 (radians) ou ± 90°. Par exemple, une tentative pour trouver l'angle entre l'axe des x et le vecteur (0, 1) nécessite l'évaluation de arctan(1/0), qui échoue à cause de la division par zéro, alors que atan2(1, 0) donne la bonne réponse π/2. Quand les calculs sont effectués à la main, les corrections de quadrant nécessaires et la gestion des exceptions peuvent être faites par observation, mais dans un programme informatique, il est extrêmement utile de disposer d'une fonction unique qui délivre toujours un résultat correct non ambigu. DéfinitionPour y ≠ 0 : où φ est l'angle compris dans [0,π/2[ tel que et sgn est la fonction signe. Et : Notes :
Cependant, cette expression devrait être plus adaptée à un usage symbolique que la définition précédente, et est néanmoins totalement inadaptée à l'utilisation en virgule flottante; la division provoque un débordement au voisinage de la partie négative de l'axe des x, et donne un NaN ou une erreur pour atan2(0,0).
La bibliothèque mathématique libre FDLIBM disponible dans netlib montre dans son code source comment implémenter atan2 avec une gestion de valeurs spéciales IEEE. Pour les systèmes ne disposant pas d'un multiplicateur matériel, la fonction DérivéeComme la fonction atan2 est fonction de 2 variables, elle possède deux dérivées partielles. Aux points où ces dérivées existent, atan2 est, à une constante près, égale à arctan(y/x). Pour x > 0 ou y ≠ 0, Donc le gradient de atan2 est donné par : IllustrationsLe diagramme ci-dessous présente les valeurs prises par atan2 sur des points remarquables du cercle trigonométrique. Les valeurs, en radians, sont inscrites en bleu à l'intérieur du cercle. Les quatre points (1,0), (0,1), (-1,0), et (0,-1) sont notés à l'extérieur du cercle. On notera que l'ordre des arguments x, y est inversé ; la fonction atan2(y,x) donne l'angle correspondant au point (x,y).  Le schéma suivant montre les valeurs prises par atan2 pour les points du cercle trigonométrique. Sur l'axe des x, on a les arguments des points. Ils partent de 0 (point (1, 0)) et vont dans le sens trigonométrique en passant par les points :
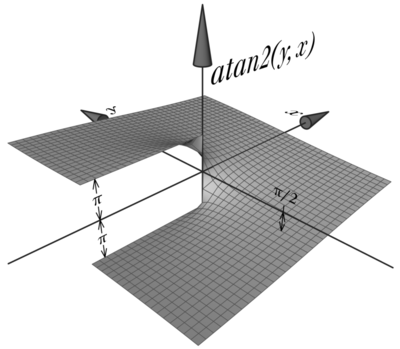
jusqu'à (1, 0) qui a pour argument 0 = 2π modulo 2π. Sur ce schéma, on peut voir clairement apparaitre la discontinuité de la fonction atan2. Quand un point z traverse la partie négative de l'axe réel — par exemple va de (0, 1) à (0, –1) en passant par (–1, 0) — son argument devrait aller de π/2 à 3π/2 en passant par π. Mais la valeur de la fonction atan2 (valeur principale de l'argument) va de π/2 à π, puis saute à –π (discontinuité), pour aller vers –π/2. Ci-dessous une vue 3D montrant la différence entre atan2(y, x) et arctan(y/x). Référence(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « atan2 » (voir la liste des auteurs).
Liens externes
|



]=\operatorname {Arg} (x+\mathrm {i} \,y)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7f4bff7d5c7bf45e7af86b06051f36094f52c73)







![{\displaystyle {\displaystyle {\begin{aligned}&{\frac {\partial }{\partial x}}\operatorname {atan2} (y,\,x)={\frac {\partial }{\partial x}}\arctan \left({\frac {y}{x}}\right)=-{\frac {y}{x^{2}+y^{2}}},\\[5pt]&{\frac {\partial }{\partial y}}\operatorname {atan2} (y,\,x)={\frac {\partial }{\partial y}}\arctan \left({\frac {y}{x}}\right)={\frac {x}{x^{2}+y^{2}}}.\end{aligned}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77098fe4e09d555445f0d3108a09eb038c3d1de9)
![{\displaystyle {\displaystyle {\begin{aligned}&{\frac {\partial }{\partial x}}\operatorname {atan2} (y,\,x)={\frac {\partial }{\partial x}}\arctan \left({\frac {y}{x}}\right)=1/[(y/x)^{2}+1].{\frac {\partial }{\partial x}}[y/x]=1/[(y/x)^{2}+1].y.{\frac {\partial }{\partial x}}[1/x]=1/[(y/x)^{2}+1].y.(-1)/(x^{2})\end{aligned}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/feed016c618042ddf3dd6f6277885f67845c0e98)
![{\displaystyle {\displaystyle {\begin{aligned}&{\frac {\partial }{\partial y}}\operatorname {atan2} (y,\,x)={\frac {\partial }{\partial y}}\arctan \left({\frac {y}{x}}\right)=1/[(y/x)^{2}+1].{\frac {\partial }{\partial y}}[y/x]=1/[(y/x)^{2}+1].(1/x).\end{aligned}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c4d7edf1132156cb2531ad85a9f8842168ee2d2)


![{\displaystyle \left]-{\frac {\pi }{2}},\,{\frac {\pi }{2}}\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d04069022bbf825c4d34726647e9029a7d6f66e3)
![{\displaystyle ]-\pi ,\,\pi ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20a5caeb9a1af1820728dae527a626bf40f64eef)