Algorithme de Thompson

En informatique théorique plus précisément en théorie des langages, l'algorithme de Thompson est un algorithme qui, étant donné une expression régulière, crée un automate fini qui reconnaît le langage décrit par cette expression. Il est nommé ainsi d'après Ken Thompson qui l'a décrit en 1968[1].

Contexte

Le théorème de Kleene affirme que l'ensemble des langages rationnels sur un alphabet ${\displaystyle A}$ est exactement l'ensemble des langages sur ${\displaystyle A}$ reconnaissables par automate fini. Il existe des algorithmes pour passer de l'un à l'autre. L'algorithme de Thompson permet d'aller de l'expression à l'automate, tout comme la construction de Glushkov. L'algorithme de McNaughton et Yamada permet d'aller dans l'autre sens.

Description

L'algorithme consiste à construire l'automate petit à petit, en utilisant des constructions pour l'union, l'étoile et la concaténation. Ces constructions font apparaître des epsilon transitions qui sont ensuite éliminées[2] (La méthode d'élimination des epsilon transitions est détaillée dans l'article « Epsilon transition »). À chaque expression rationnelle s est associé un automate fini N(s). Cet automate est construit par induction sur la structure de l'expression.

Cas de base

Expression rationnelle	Automate associé
Expression ε
Expression a où a est une lettre

Cas inductifs

Expression rationnelle	Automate associé
Union (s+t)
Concaténation s.t
Etoile de Kleene s*

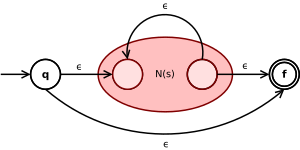
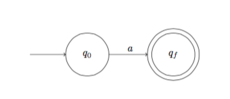
N(s) et N(t) étant les automates associés aux expressions s et t, l'automate pour l'union des deux expressions (s+t) branche depuis l'état initial q soit dans N(s) soit dans N(t). Pour une concaténation s.t, on place les automates N(s) et N(t) en séquence. Pour l'étoile de Kleene, s*, on construit un automate qui boucle sur l'automate N(s).

Exemple

Considérons par exemple le langage défini par l'expression rationnelle ${\displaystyle L=(ab+c^{*})}$. Le tableau suivant montre les étapes de construction d'un automate reconnaissant ce langage avec l'algorithme de Thompson.

	Automates
Etape 1. On construit un automate reconnaissant le langage ${\displaystyle \{a\}}$.
Etape 2. On construit un automate reconnaissant le langage ${\displaystyle \{b\}}$.
Etape 3. On construit un automate reconnaissant le langage ${\displaystyle \{c\}}$.
Étape 4. Par concaténation des automates de l'étape 1 et 2, on obtient un automate reconnaissant le langage {ab}
Etape 5. À partir de l'automate de l'étape 3, on obtient un automate reconnaissant le langage c*
Etape 6. Enfin, le langage ${\displaystyle L=(ab+c^{*})}$est reconnu par l'union de l'automate de l'étape 4 et 5.

En appliquant un post-traitement pour supprimer les epsilon transitions, on obtient un automate avec moins d'états reconnaissant le même langage :

Automate sans epsilon transitions.

Complexité

Taille de l'automate

On peut donner une majoration de la taille de l’automate en fonction de la taille de l'expression. La taille |e| d'une l'expression e est mesurée par le nombre de symboles qui y figurent, à l'exception des parenthèses. Donc

${\displaystyle |\emptyset |=|\varepsilon |=|a|=1,\ |s+t|=|s\cdot t|=|s|+|t|+1,\ |s^{*}|=1+|s|}$.

Notons n(s) le nombre d'états de l'automate N(s). Alors

${\displaystyle n(\emptyset )=n(\varepsilon )=n(a)=2,\ n(s+t)=n(s)+n(t)+2,\ n(s\cdot t)=n(s)+n(t)-1,\ n(s^{*})=2+n(s)}$.

Dans tous les cas, on a donc

${\displaystyle n(s)\leq 2|s|}$,

en d'autres termes, le nombre d'états est au plus deux fois la taille de l'expression.

Pour le nombre de transitions, un argument encore plus simple s'applique : de chaque état sortent au plus deux flèches, donc le nombre de transitions est au plus le double du nombre d'états.

Place prise par l'automate

Dès la première présentation de l’algorithme, utilisé dans des commandes comme grep, l'automate est implémenté par un tableau qui, pour chaque état, contient deux informations : soit ce sont deux numéros d'états, et alors les transitions correspondantes sont des epsilon transitions, soit c'est une lettre et un état, et dans ce cas c'est une transition par une lettre. Cette représentation est très compacte.

Complexité en temps

En supposant connus les automates finis N(s) et N(t) associés à deux expressions régulières s et t, la construction de l'automate associé à l'union (s+t) ou la concaténation (s.t) s'effectue en temps constant (c'est-à-dire qui ne dépend pas de la taille des expressions régulières, ni des automates). De même pour la construction de l'automate associé à l'étoile de Kleene (s*).

Par conséquent, la construction de l'automate associé à une expression de taille n s'effectue en ${\displaystyle \Theta (n)}$.

Pour la suppression des epsilon-transitions, la complexité est celle du calcul d'une fermeture transitive^[C'est-à-dire ?] (voir l'article « Epsilon transition » ).

Notes et références

1. Thompson 1968.
2. Jacques Désarménien, « Chapitre 1 : Automates finis », sur Institut d'électronique et d'informatique Gaspard-Monge.

Bibliographie

• (en) Ken Thompson, « Regular expression search algorithm », Comm. Assoc. Comput. Mach., vol. 11,‎ 1968, p. 419–422
• (en) Robert McNaughton et Hisao Yamada, « Regular expressions and state graphs for automata », IRE Trans. Electronic Computers, vol. EC-9, n^o 1,‎ janvier 1960, p. 39-47 (DOI 10.1109/TEC.1960.5221603)

Liens externes

• Matthew Naylor, « Animation of Thompson construction », sur université de York
• Jean-Baptiste Priez, « Algorithme de Thompson » [archive du 28 mai 2016], sur Blog Kérios (consulté le 25 janvier 2016)