Triángulo de un séptimo del área

El área del triángulo rosa es una séptima parte del área del triángulo grande ABC.

En geometría plana, cualquier triángulo ABC contiene un triángulo de una séptima parte del área de ABC, formado de la siguiente manera: los lados de este triángulo se encuentran en las cevianas p, q y r, de forma que:

p conecta A con un punto en BC que es un tercio de la distancia de B a C ,
q conecta B con un punto en CA que es un tercio de la distancia de C a A ,
r conecta C con un punto en AB que es un tercio de la distancia de A a B.

La prueba de la existencia del triángulo de una séptima parte del área se demuestra a partir de la construcción de seis líneas paralelas:

dos paralelas a p, una a través de C, la otra a través del corte de q.r
dos paralelas a q, una a través de A, la otra a través del corte de r.p
dos paralelas a r, una a través de B, la otra a través del corte de p.q

La idea de Hugo Steinhaus es que el triángulo (central) con lados p, q, r se refleje en sus lados y vértices.[1]​ Estos seis triángulos adicionales cubren parcialmente al ABC, y dejan seis triángulos adicionales que sobresalen fuera del ABC. Centrándose en el paralelismo de la construcción completa (publicada por Martin Gardner a través de la revista en línea de James Randi), son evidentes las congruencias entre pares de piezas sobresalientes y faltantes de ABC . Como se ve en la solución gráfica, las seis piezas más la original equivalen a todo el triángulo ABC.[2]​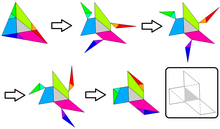

Graphical solution to the one-seventh area triangle problem.
La congruencia de las longitudes de los bordes permite que la rotación de los triángulos seleccionados forme tres paralelogramos de áreas iguales, que se dividen en seis triángulos de igual tamaño al triángulo interior original.

Robert Potts incluyó una muestra temprana de esta construcción geométrica y cálculo de área en 1859, en su libro de texto sobre geometría euclidiana.[3]​

Según Cook y Wood (2004), este triángulo desconcertó a Richard Feynman en una conversación durante una cena; lo que llevó a los comensales a dar cuatro demostraciones diferentes de la relación entre las áreas.[4]​ De Villiers (2005) halló una generalización y un resultado análogo para un paralelogramo.[5]​

Un resultado más general basado en una construcción similar es conocido como el teorema de Routh.

Referencias

  1. ↑ Hugo Steinhaus (1960) Mathematical Snapshots
  2. ↑ James Randi (2001) That Dratted Triangle, proof by Martin Gardner
  3. ↑ Robert Potts (1859) Euclid's Elements of Geometry, Fifth school edition, problems 59 and 100, pages 78 & 80 via Internet Archive
  4. ↑ R.J. Cook & G.V. Wood (2004) "Feynman's Triangle", Mathematical Gazette 88:299–302
  5. ↑ Michael de Villiers (2005) "Feynman's Triangle: Some Feedback and More" Archivado el 3 de marzo de 2016 en Wayback Machine. Mathematical Gazette 89:107

Enlaces externos