|
Ruptura espontánea de simetríaEn física la ruptura espontánea de la simetría ocurre cuando un sistema definido por una lagrangiana simétrica respecto a un grupo de simetría cae en un estado vacío que no es simétrico. Cuando eso sucede el sistema no se comporta más de forma simétrica.[1][2][3] En particular, puede describir sistemas en los que las ecuaciones de movimiento o el Lagrangiano obedecen simetrías, pero las soluciones de vacío de menor energía no presentan esa misma simetría. Cuando el sistema pasa a una de esas soluciones de vacío, la simetría se rompe para las perturbaciones alrededor de ese vacío aunque todo el Lagrangiano conserve esa simetría. El grupo de simetría puede ser discreto como el grupo espacial de un cristal, o continuo como un grupo de Lie como la simetría rotacional del espacio. Sin embargo, si el sistema solo tiene una dimensión espacial entonces solo las simetrías discretas pueden romperse en un estado vacío de la teoría cuántica, aunque también una solución clásica puede romper una simetría continua. La ruptura de la simetría conlleva la aparición de nuevas partículas (asociados a nuevos términos de masas en el nuevo lagrangiano como los bosones de Nambu-Goldstone o los bosones de Higgs) y la aparición de términos de masas de partículas ya existentes en el lagrangiano. Un ejemplo común para explicar este fenómeno es el de un balón situado en reposo en la cima de una colina lo cual significa que el balón está en un estado de simetría, sin embargo, este estado es inestable ya que a la menor perturbación el balón rodaría abajo de la colina en una dirección particular alrededor de la cima. Descripción generalPor definición, la ruptura espontánea de simetría requiere la existencia de leyes físicas (por ejemplo, mecánica cuántica) que sean invariantes bajo una transformación de simetría (como traslación o rotación), de modo que cualquier par de resultados que difieran sólo por esa transformación tengan la misma distribución de probabilidad. Por ejemplo, si las medidas de un observable en dos posiciones diferentes cualesquiera tienen la misma distribución de probabilidad, el observable tiene simetría traslacional. La ruptura espontánea de la simetría se produce cuando esta relación se rompe, mientras que las leyes físicas subyacentes siguen siendo simétricas. Por el contrario, en la ruptura explícita de simetría, si se consideran dos resultados, las distribuciones de probabilidad de un par de resultados pueden ser diferentes. Por ejemplo, en un campo eléctrico, las fuerzas sobre una partícula cargada son diferentes en diferentes direcciones, por lo que la simetría rotacional se rompe explícitamente por el campo eléctrico que no tiene esta simetría. Las fases de la materia, como los cristales, los imanes y los superconductores convencionales, así como las transiciones de fase simples, pueden describirse mediante la ruptura espontánea de la simetría. Algunas excepciones notables son las fases topológicas de la materia, como el efecto Hall cuántico fraccionario. Típicamente, cuando se produce la ruptura espontánea de simetría, las propiedades observables del sistema cambian de múltiples maneras. Por ejemplo, se espera que la densidad, la compresibilidad, el coeficiente de expansión térmica y el calor específico cambien cuando un líquido se convierte en sólido. Mecanismos que llevan a la ruptura de la simetríaMecanismo de Nambu-GoldstoneEste mecanismo se aplica al caso de una ruptura de simetría gauge global, como caso particular y sencillo de simetría gauge local. Si la es invariante bajo una cierta simetría pero el estado del vacío , no entonces se dice que el sistema tiene una "simetría en modo Goldstone" y conlleva la existencia de campos extras.
Se puede demostrar que si partículas sin masa (bosones de Nambu-Goldstone).[4][5] EjemplosPotencial del sombreroVéase también: Mecanismo de Coleman-Weinberg
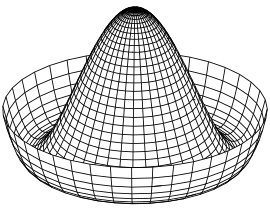 Consideremos una cúpula simétrica ascendente con un canal que rodea la parte inferior. Si se coloca una bola en la cúspide de la cúpula, el sistema es simétrico con respecto a una rotación alrededor del eje central. Pero la bola puede romper espontáneamente esta simetría rodando por la cúpula hasta la depresión, un punto de mínima energía. Después, la pelota se detiene en un punto fijo del perímetro. La cúpula y la pelota conservan su simetría individual, pero el sistema no.[6] En el modelo relativista idealizado más sencillo, la simetría rota espontáneamente se resume mediante una teoría de campos escalares ilustrativa. El Lagrangiano relevante de un campo escalar , que esencialmente dicta cómo se comporta un sistema, puede dividirse en términos cinéticos y potenciales,
Es en este término potencial donde se desencadena la ruptura de simetría. Un ejemplo de potencial, debido a Jeffrey Goldstone[7] se ilustra en el gráfico de la izquierda.
Este potencial tiene un número infinito de posibles mínimos (estados de vacío) dados por:
para cualquier real θ entre 0 y 2π. El sistema también tiene un estado de vacío inestable correspondiente a Φ = 0. Este estado tiene una simetría de U(1). Sin embargo, una vez que el sistema cae en un estado de vacío estable específico (que equivale a una elección de θ), esta simetría parecerá perderse, o "romperse espontáneamente". De hecho, cualquier otra elección de θ tendría exactamente la misma energía, y las ecuaciones definitorias respetan la simetría, pero el estado base (vacío) de la teoría rompe la simetría, lo que implica la existencia de un Bosón de Nambu-Goldstone sin masa, el modo que corre alrededor del círculo en el mínimo de este potencial, e indica que hay algún recuerdo de la simetría original en el Lagrangiano.[8][9] Ejemplo matemáticoUn campo roto espontáneamente se describe mediante una teoría de campo escalar. En física, podemos ver la ruptura de simetría a través del lagrangiano y es en el término potencial (V(φ)) donde la acción de la ruptura de simetría ocurre. Un ejemplo de un potencial se muestra en la gráfica de la derecha. Este potencial tiene varios estados vacíos mínimos posibles dados por para alguna θ real entre 0 2π. El sistema también tiene un estado vacío inestable correspondiente a Φ = 0. Este estado simetría U(1). Sin embargo, en cuanto el sistema cae en un estado vacío estable específico (correspondiente a la elección de θ) esta simetría se perderá o romperá espontáneamente. Mecanismo de HiggsEn el modelo estándar, la ruptura espontánea de simetría se complementa por el uso del bosón de Higgs, que es responsable de las masas de los bosones W y Z. Todo esto puede verse de forma más técnica en la interacción de Yukawa, donde se muestra cómo obtienen masa los fermiones mediante la ruptura de simetría. Este mecanismo se aplica al caso de una ruptura de simetría gauge local. Concepto más amplioGeneralmente, podemos tener ruptura espontánea de simetría en situaciones donde no hay estados vacíos y para sistemas que no están descritos por una acción (integral en el tiempo del lagrangiano). El concepto crucial aquí es el orden del parámetro. Si existe un campo que adquiere un valor de expectación (no necesariamente en el vacío) el cual no es invariante bajo la simetría en cuestión, decimos que el sistema está en una fase ordenada y la simetría se rompe espontáneamente. Esto se debe a que otros subsistemas interactúan con un parámetro de orden el cual forma un marco de referencia contra el cual se puede medir. Si un estado vacío obedece la simetría inicial entonces se dice que el sistema está en un modo de Wigner, de otra forma se encuentra en un modo de Goldstone. Otros ejemplos
En física de partículasEn física de partículas, las partículas portadoras de fuerza se especifican normalmente mediante ecuaciones de campo con simetría gauge; sus ecuaciones predicen que ciertas medidas serán las mismas en cualquier punto del campo. Por ejemplo, las ecuaciones de campo pueden predecir que la masa de dos quarcs es constante. La resolución de las ecuaciones para hallar la masa de cada quarc puede dar dos soluciones. En una solución, el quarc A es más pesado que el quarc B. En la segunda solución, el quarc B es más pesado que el quarc A por la misma cantidad. La simetría de las ecuaciones no se refleja en las soluciones individuales, pero sí en el rango de soluciones. Una medición real refleja sólo una solución, lo que representa una ruptura de la simetría de la teoría subyacente. "Oculto" es un término mejor que "roto", porque la simetría siempre está ahí en estas ecuaciones. Este fenómeno se denomina ruptura espontánea' de la simetría (SSB) porque nada (que sepamos) rompe la simetría en las ecuaciones.[10]: 194–195 Por la naturaleza de la ruptura espontánea de la simetría, diferentes partes del Universo primitivo romperían la simetría en diferentes direcciones, dando lugar a defectos topológicos, como paredes de dominio bidimensionales, cuerdas cósmicas unidimensionales, monopolos cero-dimensionales, y/o texturas, dependiendo del grupo de homotopía relevante y de la dinámica de la teoría. Por ejemplo, la ruptura de la simetría de Higgs puede haber creado cuerdas cósmicas primordiales como subproducto. La hipotética ruptura de simetría de la GUT produce genéricamente monopolos, creando dificultades para la GUT a menos que los monopolos (junto con cualquier pared de dominio de la GUT) sean expulsados de nuestro Universo observable a través de la inflación cósmica.[11] Simetría quiralLa ruptura de simetría quiral es un ejemplo de ruptura de simetría espontánea que afecta a la simetría quiral de las interacciones fuertes en física de partículas. Es una propiedad de la cromodinámica cuántica, la teoría cuántica de campos que describe estas interacciones, y es responsable de la mayor parte de la masa (más del 99%) de los nucleones, y por tanto de toda la materia común, ya que convierte cuarks muy ligeros ligados en constituyentes 100 veces más pesados de bariones. Los bosones de Nambu-Goldstone aproximados en este proceso espontáneo de ruptura de simetría son los piones, cuya masa es un orden de magnitud más ligera que la masa de los nucleones. Sirvió como prototipo e ingrediente significativo del mecanismo de Higgs subyacente a la ruptura de simetría electrodébil. Premio NobelEl 7 de octubre de 2008, la Real Academia Sueca de Ciencias concedió el Premio Nobel de Física a dos japoneses y a un norteamericano por su trabajo en física de partículas. Makoto Kobayashi y Toshihide Maskawa compartieron con Yoichiro Nambu el premio por descubrir el origen de la ruptura de la simetría y su mecanismo.[12] Véase también
Notas
Enlaces externos
|











