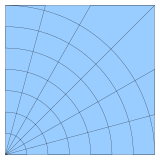
Retículo regular

Ejemplo de un retículo regular

Un retículo regular (o también cuadrícula regular, aunque no todos los retículos están formados por rectas paralelas)[1]​ es un teselado del espacio euclídeo n-dimensional formado por paralelotopos congruentes entre sí.[2]​ Su opuesto es un retículo irregular.

Son la base de procedimientos numéricos como el método de los elementos finitos, el método de los volúmenes finitos, el método de las diferencias finitas y, en general, para la discretización de espacios parametrizados. Dado que las derivadas de este tipo de variables se pueden expresar convenientemente como diferencias finitas, las cuadrículas estructuradas[3]​ aparecen principalmente en el método de las diferencias finitas. Los retículos no estructurados ofrecen más flexibilidad que las cuadrículas estructuradas y, por lo tanto, son muy útiles en el método de elementos finitos y en el método de volúmenes finitos.

Cada celda de la cuadrícula puede ser identificada por un índice (i, j) en dos dimensiones o (i, j, k) en tres dimensiones, y cada vértice tiene asignado una coordenada ${\displaystyle (i\cdot dx,j\cdot dy)}$ en 2D o ${\displaystyle (i\cdot dx,j\cdot dy,k\cdot dz)}$ en 3D para los correspondientes números reales, representando dx, dy y dz el espaciado de la cuadrícula.

Cuadrículas relacionadas

Una cuadrícula cartesiana es un caso especial, en el que los elementos son cuadrados unitarios o cubos unitarios, y los vértices son puntos de un retículo entero.[4]​

Una cuadrícula rectilínea es una teselación formada por rectángulos u ortoedros, que no son en general todos ellos congruentes entre sí. Las celdas aún pueden estar indexadas por números enteros como se indicó anteriormente, pero la correspondencia entre los índices y las coordenadas de los vértices es menos uniforme que en una cuadrícula normal. Un ejemplo de una cuadrícula rectilínea que no es regular aparece en papel grafiado con escala logarítmica.

Una cuadrícula oblicua es una teselación formada por paralelogramos o paralelepípedos en su caso. Si las longitudes de las unidades son todas iguales, es una teselación de rómbica o romboédrica).

Una cuadrícula curvilínea o cuadrícula estructurada es una cuadrícula con la misma estructura combinatoria que una cuadrícula regular, en la que las celdas son cuadriláteros o cuboides generales, en lugar de rectángulos o cuboides rectangulares.

Ejemplos de retículos

Retículo cartesiano 3-D Retículo cartesiano 3-D   Retículo rectilíneo 3-D Retículo rectilíneo 3-D   Retículo curvilíneo 2-D Retículo curvilíneo 2-D   Combinación no curvilínea de diferentes retículos curvilíneos 2-D Combinación no curvilínea de diferentes retículos curvilíneos 2-D   Retículo triangular 2-D Retículo triangular 2-D

Véase también

• Coordenadas cartesianas
• Retículo entero
• Retículo no estructurado
• Discretización

Referencias

1. Real Academia Española. «cuadrícula». Diccionario de la lengua española (23.ª edición).  1. f. Conjunto de los cuadrados que resultan de cortarse perpendicularmente dos series de rectas paralelas.
2. Uznanski, Dan. «Grid.». From MathWorld--A Wolfram Web Resource, created by Eric W. Weisstein. Consultado el 25 de marzo de 2012. 
3. J.F. Thompson, B. K . Soni & N.P. Weatherill (1998). Handbook of Grid Generation. CRC-Press. ISBN 978-0-8493-2687-5. 
4. Martin Erickson (2015). ¡Ajá! Soluciones. Ediciones SM España. pp. 463 de 277. ISBN 9788467589085. Consultado el 29 de febrero de 2024. 

• Datos: Q2646942