|
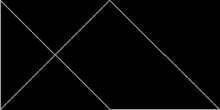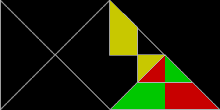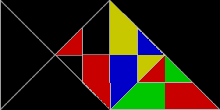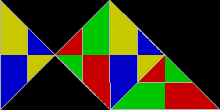
Repitesela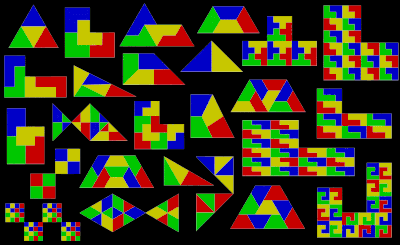 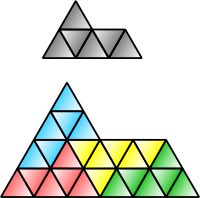 En geometría de teselaciones, una repitesela (rep-tile en inglés) es una forma que puede ser diseccionada en copias más pequeñas de sí misma. El término en inglés se acuñó como un juego de palabras a partir de repetition tiles (repeticion de teselas), del que se derivó rep-tiles, coincidente con el nombre de un conocido grupo de animales. En español se ha ideado un juego de palabras más sencillo, enlazando las palabras repite y tesela. El autor del término original en inglés fue el matemático estadounidense Solomon W. Golomb, quien lo utilizó para describir las teselas autoreplicantes.[1] Lee Sallows introdujo en 2012 una generalización del concepto con el nombre de conjunto autoteselado en la revista Mathematics Magazine.[2] TerminologíaUna repitesela se denomina de orden rep-n si su disección está formada por n copias de sí misma. Al igual que una prototesela forma un recubrimiento del plano (en muchos casos, del tipo aperiódico), la disección de una repitesela que utiliza tamaños diferentes de la forma original se denomina una repitesela irregular o irrepitesela. Si su disección utiliza n copias, dicha forma se denomina de orden irrep-n. Si todas estas subdivisiones son de medidas diferentes, entonces el enladrillado es además descrito como perfecto (véase cuadratura del cuadrado). Una forma que es rep-n o irrep-n es también de forma automática irrep-(kn − k + n) para cualquier k > 1, simplemente reemplazando la pieza más pequeña de la rep-n disección por n teselas más pequeñas. El orden de una forma, tanto utilizando repiteselas como irrepiteselas, es su número de subdivisiones más pequeño posible. Ejemplos Cada cuadrado, rectángulo, paralelogramo, rombo, o triángulo es de orden rep-4. El polidiamante esfinge (ilustrado arriba) es rep-4 y rep-9, y es uno de pocos pentágonos autoreplicantes conocidos. La curva de Gosper es de orden rep-7. El copo de nieve de Koch es irrep-7: seis pequeños copos de nieve de la misma medida, junto con otro copo con tres veces el área del más pequeño, pueden combinarse para formar un solo copo de nieve más grande. Un triángulo rectángulo con las longitudes de sus catetos en la proporción 1:2 es rep-5, y su rep-5 disección forma la base del teselado de molinillo, un recubrimiento del plano aperiódico. Aplicando el teorema de Pitágoras, se deduce que la hipotenusa (el lado inclinado del rep-5 triángulo), tiene una longitud de √5. La norma de estandarización internacional ISO 216 define medidas de hojas de papel que utilizan el valor √2, de forma que el lado largo de una hoja de papel rectangular equivale a raíz de dos veces el lado corto. Los rectángulos con esta forma son de orden rep-2. Un rectángulo (o paralelogramo) es rep-n si su relación de aspecto es √n:1. Un triángulo rectángulo isósceles es también rep-2. Repiteselas y simetríaAlgunas repiteselas, como el cuadrado y el triángulo equilátero, son simétricas y conservan idéntico aspecto cuando se reflejan en un espejo. Otras, como la esfinge, son asimétricas y existen en dos formas distintas, relacionadas entre sí por una reflexión especular. La disección de la esfinge y de algunas otras repiteselas asimétricas requiere el uso tanto de la forma original como de su forma simétrica. Repiteselas y poliformasAlgunas repiteselas están basadas en poliformas, como los polidiamantes y los poliominoes, o las formas creadas colocando cuadrados y triángulos equiláteros lado-a-lado. CuadradosSi un poliominó es rectificable, es decir, permite recubrir un rectángulo, entonces también es una repitesela, porque un rectángulo (que también es un poliominó) puede recubrir un cuadrado. Esto puede ser visto claramente en los octominoes, formados a partir de ocho cuadrados. Dos copias de algunos octominoes pueden recubrir un cuadrado; por lo tanto, estos octominoes son también repiteselas de orden rep-16.  Cuatro copias de algunos nonominoes y nonareyes recubren un cuadrado; por lo tanto, estas poliformas son también repiteselas de orden rep-36.  Triángulos equiláterosDe modo parecido, si un polidiamante recubre un triángulo equilátero, entonces también es una repitesela.  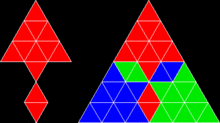 Triángulos rectángulosLas poliformas basadas en triángulos rectángulos isósceles, con ángulos de 45°, 90° y 45°, son conocidas como poliábolos. Un número infinito de ellos son repiteselas. De hecho, la más sencilla de todas las repiteselas es el propio triángulo rectángulo isósceles solo. Es de orden rep-2 cuando es dividido por un segmento que biseca el ángulo recto hasta alcanzar la hipotenusa. Las teselas de orden rep-2 lo son también de orden rep-2n (rep-4, 8, 16, 32...). Estas sucesivas particiones se obtienen dividiendo cada triángulo resultante de la división anterior en dos mitades simétricas. En otras palabras, bastan dos copias de un triángulo rectángulo isósceles para recubrir el original. Una de estas nuevas repiteselas recuerda al "pez" formado por tres triángulos equiláteros. 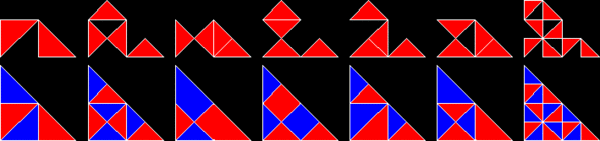
Repiteselas pentagonales Las formas de repiteselas triangulares y cuadrangulares son comunes, pero no así las pentagonales. Durante mucho tiempo, se pensaba de forma general que la esfinge era el único ejemplo conocido, pero el matemático germano-neozelandés Karl Scherer Archivado el 2 de diciembre de 2017 en Wayback Machine. y el matemático estadounidense George Sicherman han encontrado más ejemplos, incluyendo una doble-pirámide y un versión elongada de la esfinge. Estas repiteselas pentagonales han sido ilustradas en las páginas de Math Magic Archivado el 9 de diciembre de 2015 en Wayback Machine., supervisadas por el matemático estadounidense Erich Friedman.[3] Sin embargo, la esfinge y sus versiones extendidas son las únicas formas pentagonales conocidas que pueden ser repiteseladas utilizando subdivisiones del mismo tamaño. (Véanse las Páginas de repiteselas de Clarke). Repiteselas y fractalesRepiteselas como fractalesEs habitual que a partir de repiteselas puedan crearse fractales, o formas autosimilares en escalas más pequeñas y más pequeñas cada vez. Una repitesela fractal se genera subdividiendo la forma original, eliminando una o más piezas de la subdivisión, y continuando así recursivamente. Por ejemplo, la alfombra de Sierpinski está formada de este modo, partiendo de un repiteselado de un cuadrado utilizando 27 cuadrados más pequeños, y el triángulo de Sierpinski está formado a partir de un triángulo equilátero subdividido en cuatro triángulos más pequeños. Si se descarta una de las cuatro subdivisiones, se puede utilizar un triominó en forma de L (de orden rep-4) para crear cuatro fractales, dos de los cuales son idénticos excepto en su orientación.
Fractales como repiteselasDebido a que los fractales son autosimilares a escalas cada vez más pequeñas, muchos son también autoteselados, y por lo tanto, repiteselas. Por ejemplo, el triángulo de Sierpinski es un repiteselado de orden rep-3, y la alfombra de Sierpinski es de orden rep-8.
Repiteselas con múltiples repiteseladosMuchos de los repiteselados son de orden rep-n2 para cualquier valor entero positivo de n. En particular, esto es cierto para tres trapezoides, incluyendo el formado por tres triángulos equiláteros, para tres hexágonos de ejes paralelos (el L-triominó, el L-tetraminó, y el P-pentominó), y la esfinge hexadiamante.[4] Teselado infinitoEntre los polígonos regulares, solo el triángulo y el cuadrado pueden ser diseccionados en copias más pequeñas de sí mismos, con la condición de que todas sean del mismo tamaño. Sin embargo, un hexágono regular puede ser diseccionado en seis triángulos equiláteros, cada uno de los cuales puede ser diseccionado en un hexágono regular y en tres triángulos equiláteros más. Este hecho es la base de un teselado infinito del hexágono con hexágonos. El hexágono es por lo tanto una irrepitesela de orden irrep-∞ (o irrep-infinito).  Véase tambiénNotas
Error en la cita: La etiqueta <ref> definida en las <references> con nombre «FOOTNOTENiţică2003» no se utiliza en el texto anterior.Referencias
Enlaces externosRepiteselas
Irrepiteselas
|