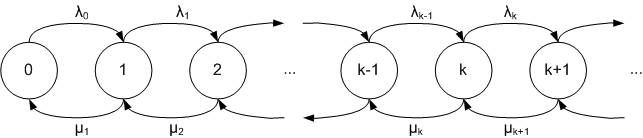
Proceso de nacimiento-muerte

El proceso de nacimiento-muerte (o proceso de nacimiento y muerte) es un caso especial del proceso de Markov de tiempo continuo donde las transiciones entre estados son de solo dos tipos: "nacimientos", que aumentan la variable de estado en uno y "muertes", que disminuyen el estado en uno. El nombre del modelo proviene de una aplicación común, el uso de dichos modelos para representar el tamaño actual de una población donde las transiciones son nacimientos y muertes literales. Los procesos de nacimiento-muerte tienen muchas aplicaciones en demografía, teoría de colas, ingeniería de desempeño, epidemiología, biología y otras áreas. Se pueden utilizar, por ejemplo, para estudiar la evolución de bacterias, el número de personas con una enfermedad dentro de una población o el número de clientes en la cola del supermercado.

Cuando ocurre un nacimiento, el proceso pasa del estado n al n + 1. Cuando ocurre una muerte, el proceso pasa del estado n al estado n − 1. El proceso está especificado por las tasas de natalidad ${\displaystyle \{\lambda _{i}\}_{i=0\dots \infty }}$ y tasas de mortalidad ${\displaystyle \{\mu _{i}\}_{i=1\dots \infty }}$ .

Ecuaciones de balanceo

Recordemos que un proceso nacimiento-muerte se caracteriza por ser una cadena de Markov con un espacio de estados ${\displaystyle S=\{0,1,...,I\}}$ donde todas las transiciones se dan entre estados adyacentes de la cadena. La distribución de probabilidad asociada al estado i-ésimo entonces adquiere la forma siguiente:

${\displaystyle \pi _{i}\lambda _{i}=\pi _{i+1}\mu _{i+1}}$

Y la condición de normalización es la siguiente: ${\displaystyle \sum _{i=0}^{I}\pi _{i}=1}$ . Se pueden resolver las ecuaciones como sigue:

${\displaystyle \pi _{i}=\pi _{0}\prod _{j=1}^{i}{\frac {\lambda _{j-1}}{\mu _{j}}}}$

Si aplicamos la condición de normalización se tiene que:

${\displaystyle 1=\pi _{0}\sum _{i=0}^{I}\prod _{j=1}^{i}{\frac {\lambda _{j-1}}{\mu _{j}}}\Rightarrow \pi _{0}=\left(\sum _{i=0}^{I}\prod _{j=1}^{i}{\frac {\lambda _{j-1}}{\mu _{j}}}\right)^{-1}}$

En consecuencia sabemos que si se satisface la condición:

${\displaystyle \sum _{i=0}^{I}\prod _{j=1}^{i}{\frac {\lambda _{j-1}}{\mu _{j}}}<\infty }$

La distribución estacionaria existe.

Referencias

• Latouche, G.; Ramaswami, V. (1999). «Quasi-Birth-and-Death Processes». Introduction to Matrix Analytic Methods in Stochastic Modelling (1st edición). ASA SIAM. ISBN 0-89871-425-7. 
• Nowak, M. A. (2006). Evolutionary Dynamics: Exploring the Equations of Life. Harvard University Press. ISBN 0-674-02338-2. 
• Virtamo, J. «Birth-death processes». 38.3143 Queueing Theory. Consultado el 2 de diciembre de 2019. 

Enlaces externos

• Karl Grill: Theorie Stochastischer Prozesse (en alemán)
• H. Dinges: Stochastik für Informatiker (en alemán)