|
Polinomios de MacdonaldEn matemáticas, los polinomios de Macdonald Pλ(x; t,q) son una familia de polinomios ortogonales simétricos en varias variables, introducidos por Macdonald en 1987. Más tarde introdujo una generalización no simétrica en 1995. Macdonald originalmente asoció sus polinomios con pesos λ de sistemas de raíz finitos y usó solo una variable t, pero luego se dio cuenta de que es más natural asociarlos con un sistema de raíces afines en lugar de con un sistema de raíces finitas, en cuyo caso la variable t puede ser reemplazada por varias variables diferentes t=(t1,...,tk), una para cada una de las órbitas k de las raíces en el sistema de raíces afines. Los polinomios de Macdonald son polinomios en n variables x=(x1,...,xn), donde n es el rango del sistema de raíces afines. Generalizan muchas otras familias de polinomios ortogonales, como el polinomio de Jack, el polinomio de Hall-Littlewood y los polinomios de Askey-Wilson, que a su vez incluyen la mayoría de los polinomios ortogonales de una variable nombrados como casos especiales. Los polinomios de Koornwinder son polinomios de Macdonald de ciertos sistemas de raíces no reducibles. Tienen relaciones profundas con álgebra de Hecke afín y con el esquema de Hilbert, que se utilizaron para probar varias conjeturas hechas por Macdonald sobre ellos. DefiniciónPrimero, para manejar con mayor facilidad las expresiones, debe establecerse una notación específica:
Los polinomios de Macdonald Pλ para λ ∈ P+ están definidos únicamente por las siguientes dos condiciones:
En otras palabras, los polinomios de Macdonald se obtienen ortogonalizando la base obvia para AW. La existencia de polinomios con estas propiedades es fácil de demostrar (para cualquier producto interior). Una propiedad clave de los polinomios de Macdonald es que son ortogonales: 〈Pλ, Pμ〉 = 0 siempre que λ ≠ μ. Esta no es una consecuencia trivial de la definición porque P+ no está totalmente ordenado, por lo que tiene muchos elementos que no son comparables. Por tanto, hay que comprobar que los polinomios correspondientes siguen siendo ortogonales. La ortogonalidad se puede probar mostrando que los polinomios de Macdonald son vectores propios para un álgebra de conmutación de operadores autoadjuntos con espacios propios unidimensionales, y utilizando el hecho de que los espacios propios para diferentes valores propios deben ser ortogonales. En el caso de sistemas de raíces no simplemente entrelazados (B, C, F, G), el parámetro t se puede elegir para variar con la longitud de la raíz, dando una familia de tres parámetros de polinomios de Macdonald. También se puede extender la definición al sistema raíz no reducido BC, en cuyo caso se obtiene una familia de seis parámetros (una t para cada órbita de las raíces, más q) conocida como los polinomios de Koornwinder. A veces es mejor considerar que los polinomios de Macdonald dependen de un sistema de raíces afines posiblemente no reducido. En este caso, hay un parámetro t asociado a cada órbita de raíces en el sistema de raíces afines, más un parámetro q. El número de órbitas de las raíces puede variar de 1 a 5. Ejemplos
Conjetura del término constante de MacdonaldSi t = qk para algún entero positivo k, entonces la norma de los polinomios de Macdonald viene dada por Esto fue conjeturado por Macdonald (1982) como una generalización de la conjetura de Dyson, y Cherednik (1995) lo demostró para todos los sistemas de raíces (reducidos) usando las propiedades del álgebra de Hecke doblemente afín. La conjetura había sido probada previamente caso por caso para todos los sistemas de raíces excepto los del tipo En por varios autores. Hay otras dos conjeturas que, junto con la conjetura de la norma, se denominan colectivamente conjeturas de Macdonald en este contexto: además de la fórmula de la norma, Macdonald conjeturó una fórmula para el valor de Pλ en el punto tρ, y una simetría Nuevamente, fueron probadas para sistemas de raíces reducidos generales por (Cherednik, 1995), usando álgebras de Hecke doblemente afines, y la extensión al caso BC siguió poco después a través del trabajo de van Diejen, Noumi y Sahi. Conjetura de positividad de MacdonaldEn el caso de sistemas de raíces del tipo An−1 los polinomios de Macdonald son simplemente polinomios simétricos en n variables con coeficientes que son funciones racionales de q y t. Cierta versión transformada de los polinomios de Macdonald (véase la fórmula combinatoria a continuación) forma una base ortogonal del espacio de funciones simétricas sobre y, por lo tanto, se puede expresar en términos de funciones de Schur . Los coeficientes Kλμ(q,t) de estas relaciones se denominan coeficientes de Kostka–Macdonald o coeficientes qt-Kostka. Macdonald conjeturó que los coeficientes de Kostka y Macdonald eran polinomios en q y t con coeficientes enteros no negativos. Estas conjeturas están ahora probadas; el paso más difícil y final fue probar la positividad, lo que hizo Mark Haiman (2001), al probar la conjetura n!. Todavía es un problema central abierto en la combinatoria algebraica encontrar una fórmula combinatoria para los coeficientes qt-Kostka. Conjetura n!La conjetura n! de Adriano Garsia y Mark Haiman establece que para cada partición μ de n, el espacio abarcado por todas las derivadas parciales superiores de tiene dimensión n!, donde (pj, qj) recorre los n elementos del diagrama de la partición μ, considerado como un subconjunto de los pares de enteros no negativos. Por ejemplo, si μ es la partición 3 = 2 + 1 de n = 3 entonces los pares (pj, qj) son (0, 0), (0, 1), (1, 0), y el espacio Dμ está dividido por que tiene dimensión 6 = 3!. ¡La prueba de Haiman de la conjetura de positividad de Macdonald y la conjetura n! implicaba mostrar que el esquema de Hilbert isoespectral de n puntos en un plano era de Cohen–Macaulay (e incluso de Gorenstein). Los resultados anteriores de Haiman y Garsia ya habían demostrado que esto implicaba la conjetura n!, y que la conjetura n! implicaba que los coeficientes de Kostka–Macdonald eran multiplicidades de caracteres graduadas para los módulos Dμ. Esto implica inmediatamente la conjetura de positividad de Macdonald porque las multiplicidades de caracteres tienen que ser números enteros no negativos. Ian Grojnowski y Mark Haiman encontraron otra prueba de la conjetura de positividad de Macdonald al demostrar una conjetura de positividad para el polinomio LLT. Fórmula combinatoria para los polinomios de MacdonaldEn 2005, J. Haglund, M. Haiman y N. Loehr[1] dieron la primera prueba de una interpretación combinatoria de los polinomios de Macdonald. En 1988, I. G. Macdonald[2] dio la segunda prueba de una interpretación combinatoria de los polinomios de Macdonald (ecuaciones (4.11) y (5.13)). La fórmula de Macdonald es diferente a la del trabajo de Haglund, Haiman y Loehr, con muchos menos términos (esta fórmula también se demuestra en el trabajo seminal de Macdonald,[3] Ch. VI (7.13)). Si bien es muy útil para el cálculo e interesante por derecho propio, sus fórmulas combinatorias no implican inmediatamente la positividad de los coeficientes de Kostka-Macdonald, ya que dan la descomposición de los polinomios de Macdonald en funciones simétricas monomiales en lugar de con funciones de Schur. Escritos en los polinomios de Macdonald transformados en lugar de los habituales , son donde σ es un relleno del diagrama de Young de forma μ, inv y maj son ciertas estadísticas combinatorias (funciones) definidas en el relleno σ. Esta fórmula expresa los polinomios de Macdonald en infinitas variables. Para obtener los polinomios en n variables, basta con restringir la fórmula a rellenos que solo usen los números enteros 1, 2, ..., n. El término xσ debe interpretarse como donde σi es el número de casillas en el relleno de μ con contenido i. 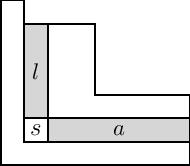 Los polinomios de Macdonald transformados en la fórmula anterior están relacionados con los polinomios de Macdonald clásicos a través de una secuencia de transformaciones. Primero, la forma integral de los polinomios de Macdonald, denominada , es una nueva escala de que permite eliminar los denominadores de los coeficientes: donde es la colección de cuadrados en el diagrama de Young de , y y denotan el brazo y la pierna del cuadrado , como se muestra en la figura. Nota: la figura de la derecha usa la notación francesa para el cuadro, que se invierte verticalmente de la notación inglesa que se usa en la página de Wikipedia para los diagramas de Young. La notación francesa se usa más comúnmente en el estudio de los polinomios de Macdonald. Los polinomios de Macdonald transformados se pueden definir en términos de los . Se tiene que donde La notación de paréntesis anterior denota la sustitución pletística. Esta fórmula se puede usar para probar la fórmula de Knop y Sahi para los polinomios de Jack. Polinomios de Macdonald no simétricosEn 1995, Macdonald introdujo un análogo no simétrico de los polinomios simétricos de Macdonald. Los polinomios de Macdonald simétricos se pueden recuperar fácilmente de la contraparte no simétrica. En su definición original, muestra que los polinomios de Macdonald no simétricos son una familia única de polinomios ortogonales con respecto a un cierto producto interno, así como satisfacer una propiedad de triangularidad cuando se expande en la base del monomio. En 2007, Haglund, Haiman y Loehr dieron una fórmula combinatoria para los polinomios de Macdonald no simétricos. Los polinomios no simétricos de Macdonald se especializan en caracteres de Demazure, tomando q=t=0, y a clave de polinomios cuando q=t=∞. Fórmulas combinatorias basadas en el proceso de exclusiónEn 2018, S. Corteel, O. Mandelshtam y L. Williams utilizaron el proceso de exclusión para brindar una caracterización combinatoria directa de los polinomios de Macdonald simétricos y no simétricos.[4] Sus resultados difieren del trabajo anterior de Haglund en parte porque dan una fórmula directamente para los polinomios de Macdonald en lugar de una transformación de los mismos. Desarrollan el concepto de una cola multilíneal, que es una matriz que contiene bolas o celdas vacías junto con una aplicación entre las bolas y sus vecinas y un mecanismo de etiquetado combinatorio. El polinomio de Macdonald no simétrico entonces satisface: donde la suma es sobre todas las colas multilíneales de tipo y es una función de ponderación que asigna esas colas a polinomios específicos. El polinomio simétrico de Macdonald satisface: donde la suma exterior se aplica sobre todas las composiciones distintas que son permutaciones de , y la suma interior es como antes. Referencias
Bibliografía
Enlaces externos
|











![{\displaystyle D_{\mu }=C[\partial x,\partial y]\,\Delta _{\mu }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d51076c672fbd20ae78ab96da9f5dcab91f3b5d)





















![{\displaystyle {\widetilde {H}}_{\mu }(x;q,t)=t^{-n(\mu )}J_{\mu }\left[{\frac {X}{1-t^{-1}}};q,t^{-1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77027622d9897fab6f2f1c735102b348a8152090)





