|
Paradoja de la escaleraLa paradoja de la escalera (o "paradoja del poste de granero") es un experimento mental de la relatividad especial, desarrollado por Rindler (1961)[1] a partir de las observaciones realizadas por Einstein[2][3] y por Lorentz.[4][5] Es un experimento mental relacionado con la paradoja de Ehrenfest.[6] Se trata de una escalera que viaja horizontalmente a una velocidad relativista (cercana a la velocidad de la luz, como por ejemplo, un valor del 90% o 0,9 c) paralela al suelo, y, por tanto, sufre una contracción de longitud de Lorentz. Ahora, debe imaginarse que la escalera pasa a través de las puertas delanteras y traseras (abiertas) de un garaje o granero, cuyo espacio interno es inferior a la longitud de la escalera (longitud en reposo), por lo que si la escalera no se moviera, no podría caber dentro del granero. Para un observador estacionario, debido a la ya mencionada contracción de Lorentz, la escalera móvil podría caber completamente dentro del edificio a medida que pasa. Sin embargo, desde el punto de vista de un observador que se mueve con la escalera, ésta no se contraerá, y es el edificio el que se contraerá y tendrá una longitud menor. Esto es lo que se conoce como (parte de) la paradoja de Ehrenfest.[6] Por lo tanto, para el observador que viaja con la escalera, esta no cabrá dentro del edificio cuando lo atraviese. Esto plantea una aparente discrepancia entre las realidades de ambos observadores. Esta paradoja, o aparente paradoja, resulta de la errónea suposición de la existencia de una simultaneidad absoluta. Se dice que la escalera cabe en el garaje, si y solo si, ambos extremos pueden colocarse simultáneamente dentro del garaje. Esta paradoja puede resolverse cuando se considera la teoría de la relatividad especial, puesto que según esta teoría la condición de simultaneidad depende de cada observador, por lo que la respuesta a si la escalera cabe dentro del garaje o no, también depende de dónde se sitúe el punto de vista o el observador, es decir, de cada uno de ellos. ParadojaLa versión más simple de la paradoja implicaría un garaje con una puerta (delantera) y una puerta (trasera) abiertas, y una escalera que, cuando se considera en reposo con respecto al garaje sería demasiado larga para caber en su interior, y cuando se considera en movimiento para un observador externo, dado que viaja al 90% de la velocidad de la luz (c) quedaría contraída lo suficiente como para caber por completo dentro del garaje o granero mientras se mueve. Es decir, cuando movemos la escalera a alta velocidad horizontal a través del garaje estacionario, la escalera sufre el efecto relativista de contracción de longitud y se vuelve significativamente más corta debido a su alta velocidad. Como resultado, cuando la escalera pasa por el garaje, queda, durante un tiempo, completamente contenida dentro de él. Si quisiéramos, durante un breve instante podríamos cerrar simultáneamente ambas puertas para demostrar que la escalera cabe en el interior del granero.[1] La aparente paradoja surge a continuación, cuando se considera la simetría de la situación. Así, un observador que se moviera con la escalera, viajaría a velocidad constante en el mismo sistema de referencia inercial de la escalera, en el que según el principio de relatividad[3] se aplican las mismas leyes de la física. Desde esta segunda perspectiva, la escalera es ahora la que permanecerá estacionaria, y será el garaje el que se mueve a gran velocidad (con respecto a la escalera y al observador situado sobre la escalera que viaja con ésta). Por lo tanto, es el garaje el que se contrae en longitud, y ahora concluiremos que es demasiado pequeño para haber podido contener completamente a la escalera cuando pasó: la escalera no cabe y no podremos cerrar ambas puertas a ambos lados de la escalera en un instante sin golpearla. Esta aparente contradicción es la paradoja de la escalera de Rindler (1961).[1]
Solución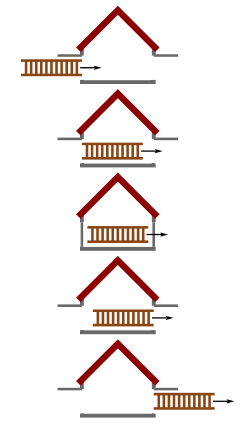 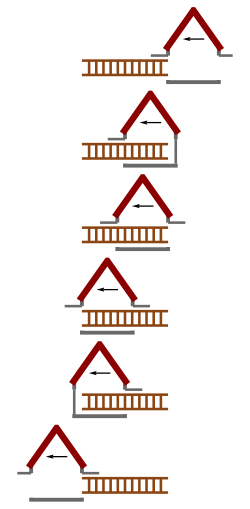 La solución a la aparente paradoja reside en considerar la relatividad, es decir, al aplicar la relatividad especial, se estaría considerando la relatividad de la simultaneidad: lo que un observador (por ejemplo, en el garaje) considera al observar dos acontecimientos simultáneos, en realidad puede no serlo para otro observador (por ejemplo, situado en la escalera). Cuando decimos que la escalera "cabe" dentro del garaje, lo que se indica precisamente es que, en un momento concreto, la posición de la parte trasera de la escalera y la posición de la parte delantera de la escalera estarán ambas dentro del garaje; o en otras palabras, tanto la parte delantera de la escalera como la trasera, estuvieron dentro del garaje de manera simultánea. Como es considerado anteriormente, la simultaneidad, en lugar de ser absoluta, es relativa, entonces, dos observadores pueden no estar de acuerdo sobre si la escalera encajaría completamente en un instante, dentro del garaje o no. Para un observador que se encontrara en el garaje, el extremo trasero de la escalera estaría en el garaje al mismo tiempo que el extremo delantero de la escalera, por lo que la escalera cabría. Pero para un observador que se encontrara en la escalera, sería el garaje el que se estaría desplazando horizontalmente, por lo que la escalera pasaría a ser más larga, o el garaje se encontraría en contracción, y la escalera no encajaría. Una forma, quizás más clara de verlo, sería considerar las puertas desde el marco de referencia del garaje, las cuales se podrían cerrar en un instante, mientras la escalera al completo, estuviera dentro. Sin embargo, desde el sistema de referencia inercial de la escalera, el primer evento es la parte frontal de la escalera, que se acerca a la puerta de salida del garaje, la puerta se cerraría, y luego se abriría para dejar pasar a la parte frontal de la escalera. Mientras, la parte trasera de la escalera habría pasado por la puerta de entrada, que se cerraría, y luego se abriría, como sucedió con la puerta de salida. Como la simultaneidad es relativa, podemos ver que no era necesario cerrar las dos puertas al mismo tiempo, sino solo la de salida, y la escalera no necesitaba caber dentro del garaje (desde un punto de vista de simultaneidad absoluto). Esta situación puede ilustrarse mejor, con el siguiente diagrama: diagrama de Minkowski. El esquema se posiciona en el marco en reposo del garaje. La banda vertical (de color azul claro) muestra el garaje en el espacio-tiempo y la banda de color rojo claro, muestra la escalera en el espacio-tiempo. Los ejes x y t son el espacio del garaje y los ejes del tiempo, respectivamente, y x′ y t′ son, en cambio, los ejes del espacio y del tiempo de la escalera, respectivamente. En el marco del garaje, la escalera puede estar representado por un conjunto de puntos en el eje horizontal, paralelos al eje x, en la banda roja. Un ejemplo es el segmento de línea azul (en negrita), que se encuentra dentro de la banda azul claro, que representa al garaje y que representa a la escalera en un momento en que está completamente dentro del garaje. Sin embargo, desde el marco de la escalera, los conjuntos de eventos simultáneos se encontrarían en líneas paralelas al eje x' por lo que, la escalera, en cualquier momento específico puede estar representada por una sección transversal de dicha línea con la banda roja. Un ejemplo de ello sería el segmento de línea roja en negrita. Aquí veremos que, dichos segmentos de línea, nunca se encuentran completamente dentro de la banda azul claro. Es decir, la escalera nunca quedaría completamente dentro del garaje.  Cerrando la escalera en el garaje En una versión más compleja de la paradoja, se puede atrapar físicamente la escalera, una vez se encuentre completamente dentro del garaje (en desplazamiento a una velocidad cercana a la de la velocidad de la luz). Por ejemplo, si no se vuelve a abrir la puerta después de cerrarla (aunque asumimos que en el marco del garaje, la puerta de salida es inamovible). De esa forma, cuando la parte frontal de la escalera golpeara la puerta de salida, diríamos que se detiene instantáneamente.[1][7] En ese momento, la puerta de entrada también se habría cerrado, por lo que la escalera quedaría atrapada dentro del garaje. Su velocidad relativa en ese instante sería 0, por lo que no se contrae en longitud, y ahora sería más largo que el garaje: tendrá que doblarse, romperse, o estallar en fragmentos (ver paradoja de Ehrenfest). Aquí surge una vez más, el enigma de considerar la situación desde el marco de referencia de la escalera. Como vimos en el análisis anterior, en su propio marco de referencia (un observador viajando con la escalera o situado sobre la escalera), la escalera siempre fue más larga que el garaje. Entonces, ¿cómo podríamos cerrar las puertas y atraparla dentro? Quizás aquí puede valer la pena señalar que hemos deducido, considerando la estructura del garaje, que efectivamente atrapamos a la escalera dentro del garaje, lo cual es una propiedad o característica general, de la relatividad. Por lo tanto, se podría pensar que esto es cierto en cualquier marco de referencia: no puede darse el caso en el que la escalera encajara en un marco pero no lo hiciera en otro. Así, desde el marco de referencia de la escalera, se tiende a pensar que debe haber alguna explicación de cómo la escalera quedó atrapada; simplemente debemos aún encontrar la explicación. La explicación que surge puede ser tal que, aunque todas las partes de la escalera desaceleren hasta 0 en el marco de referencia del garaje, dado que la simultaneidad es relativa, la correspondiente desaceleración en el marco de la escalera no es simultánea con la del marco del garaje. Por el contrario, cada parte de la escalera desacelerará de manera secuencial.[8] De esta forma, la velocidad de la escalera se irá reduciendo desde su parte frontal, a su parte posterior, hasta que finalmente la parte final de la escalera desacelere, a partir de la cual el tiempo se encuentra ya dentro del marco del garaje. Como la contracción de la longitud y la dilatación del tiempo, están ambas controladas por las transformaciones de Lorentz (desde la perspectiva del espacio-tiempo), la paradoja de la escalera puede llegar a verse como un correlato físico de la paradoja de los gemelos (en cuyo caso, uno de los gemelos del conjunto abandona la Tierra, viaja a gran velocidad durante un período de tiempo, y regresaría a la Tierra un poco más joven que el gemelo que permaneció en la Tierra).[9][10] De una forma similar, así, al caso de la escalera atrapada dentro del granero, si ninguno de los marcos de referencia es independiente (cada uno se mueve sólo en relación con el otro), ¿cómo puede ser que sea el gemelo que viajó al exterior y no el estacionario el que se observa más joven (al igual que la escalera, en lugar del granero, el más corto)? En ambos casos fue la aceleración-desaceleración, la que diferenció los fenómenos. Por ello, es el gemelo, y no la Tierra (o la escalera, no el granero) el que sufrió la fuerza de la desaceleración, al regresar a un marco temporal (o físico, en el caso de la escalera-granero), esto es, a su marco de referencia inercial.  Paradoja de la escalera y transmisión de fuerza ¿Qué sucede si la puerta trasera (la puerta por la que saldrá la escalera) se encuentra cerrada y no se abriera? Vamos a suponer que es una puerta tan sólida, que la escalera no la podría atravesar ni cuando chocara. De ese modo, en principio, solo podría detenerse. Además, como en el escenario previamente descrito, desde el marco de referencia del garaje, en un instante puede suceder que la escalera se encuentre completamente dentro del garaje o granero. Es decir, la parte trasera de la escalera, se encontrará ya dentro de los márgenes de la puerta principal (de entrada). Antes de chocar, se considera que se detiene, pero, desde el marco de referencia de la escalera, ésta es demasiado larga para caber dentro del garaje. Por ello, cuando chocara con la puerta de salida, se detendría. En ese instante, desde el marco de referencia de la escalera, su parte trasera aún no habría llegado a la puerta de entrada, mucho menos si se tiene en cuenta que el garaje estaría contraído. Aquí aparece la paradoja. La pregunta que cabría hacer es: ¿la parte trasera de la escalera cruza la puerta de entrada, o no lo hace? Surge la dificultad, fundamentalmente, al partir del supuesto de que la escalera es rígida (es decir, mantendrá la misma forma). Esto es algo fácilmente observable en la vida cotidiana. Pero al ser completamente rígida, esto significa que también puede transferir fuerza a una velocidad infinita (por lo que, cuando se empuja un extremo, el otro extremo debe reaccionar inmediatamente, de lo contrario, la escalera se deformará). Es algo que contradice a la relatividad especial, que establece que la información no podrá viajar más rápido que la velocidad de la luz (la cual es demasiado rápida para que podamos apreciarla en la vida real, pero es apreciable en el escenario de la escalera). Por lo tanto, se puede considerar que los objetos no podrán ser rígidos bajo la relatividad especial. En este último caso, cuando la parte frontal de la escalera chocara con la puerta de salida, la parte posterior de la escalera aún no habrá tenido la información que le lleve a iniciar el comportamiento de desaceleración (seguirá acelerando o desplazándose a la misma velocidad, en este caso, cercana a la velocidad de la luz). Se podría decir que, de algún modo, la escalera se "comprime", pues, tanto en el marco del garaje como en el marco inercial de la escalera, la parte trasera seguirá moviéndose en el instante de la colisión (o incluso si frenara), al menos hasta que el punto donde la parte trasera de la escalera, en su marco de referencia, entre en el cono de luz de la colisión, un punto donde la fuerza que se traslada hacia atrás a la velocidad de la luz c, desde el propio punto de colisión se encontrará con la parte distal (posterior) de la escalera. En ese punto, se puede considerar que la escalera es, en realidad, más corta que la longitud contraída originalmente, por lo que el extremo distal estará dentro del garaje. Los cálculos mostrarán que en ambos marcos de referencia, lo expuesto anteriormente es lo que sucede. No es especificado, en cambio, qué sucede después de la llegada de la fuerza a la parte posterior de la escalera (la zona que aparece coloreada de "verde" en el diagrama). A tenor de las leyes de la física, la escalera podría romperse o, si fuera lo suficientemente elástico o en función de las propiedades del material, doblarse o deformarse (volviéndose a extender hasta su longitud original o manteniendo una aceleración constante contra la puerta de salida, en el caso de ser elástico con propiedades ideales o suficientes). A una velocidad lo suficientemente alta, cualquier material realista se degradaría en muchos nodos individuales (explotaría o perdería su integridad y contigüidad física, distribuyéndose y/o dispersándose prácticamente como lo haría un gas ideal,(cita) pudiendo formar plasma o una estructura desintegrada formada por nodos independientes). "Una persona cayendo en la variación de la rejilla". Como decíamos anteriormente, esta primera versión de la paradoja fue propuesta por Wolfgang Rindler [1][7] implicaba una solución en la que una persona caminaba rápidamente, representado por una varilla, y caía en una rejilla.[11]De esa manera, al suponer que la varilla estaría completamente sobre la rejilla en el marco de referencia de la rejilla antes de que comenzara la aceleración en el eje vertical, aplicada simultáneamente y por igual a cada punto de la varilla, desde la perspectiva de la rejilla, la varilla estaría sufriendo una contracción longitudinal, y encajaría en la rejilla. Por otro lado, desde la perspectiva de la varilla, sería la rejilla la que sufriría esta contracción longitudinal, por lo que la varilla tendría una dimensión de excesivamente larga para caer.[7][11] La aceleración en el eje vertical de la varilla, siendo simultánea en el marco de referencia de la rejilla, no es, sin embargo, simultánea en el marco de referencia de la varilla. Esto se debe a que, en el marco de referencia de la varilla, la parte frontal de la varilla primero se acelera hacia abajo (como se muestra en el dibujo, en la celda 3), y, a medida que pasa el tiempo, la varilla y su marco de referencia se somete más y más a la aceleración en el eje vertical, hasta que la parte posterior de la varilla, inclusive, se acelera en el eje vertical (hacia abajo), finalmente.[7][11] Lo anterior, da como resultado un efecto de flexión en el marco de referencia de la varilla (dado que la flexión se produce en el marco del apoyo de la varilla, se puede considerar una verdadera distorsión física de la varilla, lo que provocará que se produzcan tensiones en la varilla). Esto da como resultado una flexión de la varilla en el marco de referencia de la varilla. Dado que esta flexión se produce en el marco de apoyo de la varilla, es una verdadera distorsión física de la varilla la que provocará que se produzcan tensiones en la varilla. Para que esta forma de distorsión física, o comportamiento observable (fenómeno) no rígido de la varilla, pueda ser apreciado, tanto la rejilla como la propia varilla deberán tener una escala tal que, el tiempo de recorrido, sea medible. Paradoja de la barra y el anillo Una situación particularmente similar, pero que puede ser observada como más simple que la paradoja de la varilla y la rejilla (involucrando un menor número de marcos inerciales) es la paradoja de la "barra y el anillo".[12] La paradoja de la rejilla y la varilla implica varios marcos de referencia inerciales, y una deformación secuencial de la varilla (o persona), lo cual tiende a dificultar la comprensión, introduciendo posibles aspectos mecánicos más clásicos, como son la rigidez de la varilla (o de la persona). De ese modo, una forma de observar con mayor claridad la verdadera naturaleza de la paradoja, puede ser utilizar el ejemplo de la "barra y el anillo": una barra (con una longitud ligeramente superior al diámetro del anillo) se mueve hacia arriba en el eje vertical, y hacia la derecha en el eje horizontal, mientras que el anillo se encontraría estacionario, y colocado en un plano horizontal. Si la barra describe un movimiento tal que el centro de la barra coincidiera con el centro del anillo en un instante, entonces la barra aparecerá bajo las condiciones de la contracción de Lorentz debido a un componente directo de su movimiento, y podrá pasar a través del anillo.[12] La paradoja sucede cuando esta situación se considera desde el marco de reposo de la barra, puesto que, ahora, el anillo viaja hacia abajo en el eje vertical, y hacia la izquierda en el eje horizontal, y se contraerá en ese sentido, a lo largo de su longitud horizontal, mientras que la barra, en cambio, no sufrirá contracción alguna en absoluto. ¿Cómo puede entonces pasar la barra por el anillo? La solución a la paradoja, de nuevo, se encuentra en la relatividad de la simultaneidad.[7][12] La longitud del objeto físico, pues, se define como la distancia entre 2 eventos simultáneos, que ocurren en cada uno de los extremos del objeto físico, y, dado que la simultaneidad es relativa, esta longitud también lo será. Esta variabilidad en la longitud es lo que se conoce como la contracción de Lorentz.[4] De forma similar sucede con un ángulo: un ángulo físico se define como un ángulo formado por tres eventos simultáneos, siendo este ángulo también una cantidad relativa. En la paradoja anterior, aunque la barra y el plano del anillo son paralelos en el marco de reposo del anillo, no lo serán en el marco de reposo de la barra. De ese modo, la barra no contraída pasará a través del anillo contraído por Lorentz, puesto que el plano del anillo estará girando con respecto a la barra en una cantidad suficiente, como para dejar pasar a la barra. En términos matemáticos, puede considerarse que una transformación de Lorentz se podría separar en el resultado entre el producto de una rotación espacial y una transformación de Lorentz "adecuada" (que no implica rotación espacial). La resolución matemática de la paradoja de la "barra y el anillo" se basa en el hecho de que, el producto de estas transformaciones de Lorentz "adecuadas" (horizontal y vertical) puede igualmente producir una pseudo transformación de Lorentz que no es tal (diagonal), siendo lo que se denomina "no propia", al incluir una rotación espacial (no adecuada).[12] Véase también
Referencias
Otras referencias bibliográficas
Otras lecturas relacionadas
Enlaces externos
|


