|
PSTricks
PSTricks es un conjunto de macros que permiten la inclusión de dibujos PostScript directamente dentro de código TeX o LaTeX. Originalmente fue un trabajo del Profesor Timothy Van Zandt y en años recientes lo han mantenido Denis Girou, Sebastian Rahtz y Herbert Voss. UtilizaciónPSTricks tiene una gran lista de órdenes. Las coordenadas en PSTricks siempre se representan dentro de paréntesis como ilustra el siguiente ejemplo: \begin{pspicture}(6,6)
%% Triángulo en rojo:
\psline[linecolor=red](1,1)(5,1)(1,4)(1,1)
%% Curva de Bezier en verde:
\pscurve[linecolor=green,linewidth=2pt,%
showpoints=true](5,5)(3,2)(4,4)(2,3)
%% Círculo en azul con radio 1:
\pscircle[linecolor=blue,linestyle=dashed](3,2.5){1}
\end{pspicture}
 Extensiones Las órdenes de PSTricks son de bajo nivel, así que muchos paquetes LaTeX se ha desarrollado para facilitar la creación de algunas clases de gráficos que se usan en matemáticas, como es el caso de pst-plot que provee opciones para crear gráficos de funciones, como muestra el siguiente listado de ejemplo de la función seno: \begin{pspicture*}(-7.5,-3)(7.5,3)
\psaxes[labels=none](0,0)(-7,-2)(7,2) % Establece los ejes
\psplot[linecolor=blue, linewidth=1.5pt]% % Grafica una onda sinusoidal
{-7}{7}{x 0.01745329252 div sin} % Observar la expresión en Notación Polaca Inversa
\uput[45](3.1415926,0){$\pi$} % Estas son las etiquetas
\uput[90](-1.570796,0){$-\pi/2$} % La orden \uput coloca una caja posicionada en [ángulo]
\uput[-90](1.570796,0){$\pi/2$} % relativo a la coordenada (x,y)
\uput[-135](-3.1415926,0){$-\pi$} % y poniendo el { contenido } dentro de la caja
\psline[linewidth=1pt,linecolor=red,linestyle=dotted]% % Línea punteada roja
(1.57079632,1)(1.57079632,0)
\psline[linewidth=1pt,linecolor=red,linestyle=dotted]%
(-1.57079632,-1)(-1.57079632,0)
\end{pspicture*}
El ejemplo previo también ilustra que las órdenes TeX pueden usarse como elementos dentro de las figuras. Ya que PostScript usa el estilo notación polaca inversa para las operaciones matemáticas, el argumento de pst-plot debe proveerse de esa forma. Una alternativa es utilizar el argumento opcional algebraic, entonces la expresión de la fórmula puede describirse con una notación algebraica estándar. pstricks-add extiende pst-plot para utilizar gráficos en coordenadas polares y permitiendo el uso de notación algebraica estándar en vez de notación polaca inversa. pst-math provee funciones trigonométricas en radianes (ya que PostScript usa por defecto grados) y funciones hiperbólicas. pst-3dplot se usa para crear gráficos 3D como por ejemplo: 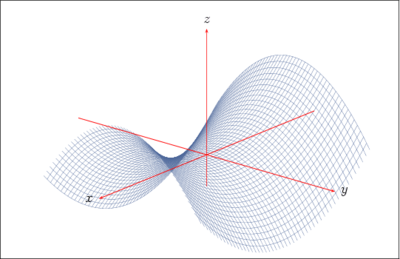 multido provee una funcionalidad básica para generar mediante lazos gráficos con elementos repetitivos:  pst-eucl es una extensión en fase de desarrollo (beta) para facilitar la creación de dibujos geométricos.  Existen más extensiones, para dibujar circuitos, código de barras, gráficos matemáticos, árboles y grafos, visualización de datos, etc. La representación geométrica de las funciones de segundo grado, mediante las transformaciones geométricas elementales como son la traslación y rotación de ejes coordenados establecen el manejo de información espacial que por medio de la visualización y que gracias al uso del software Matemático Geogebra se logra analizar, ubicar, orientar y distribuir el espacio. Los sistemas geométricos se construyen a través de la exploración activa y modelación computacional del espacio para los objetos estáticos como para los dinámicos. Efectuando desplazamientos, medidas, cálculos espaciales, etc. Para representar los sistemas algebraicos, se puede crear una variedad de imágenes y gráficas dinámicas e interactivas. CompatibilidadPSTricks solo es totalmente compatible con sistemas TeX que usen PostScript, incluyendo eTeX y otros. Sin embargo, no es compatible con el motor pdfTeX en modo PDF. Como pdfTeX es el motor por defecto de la mayoría de las aplicaciones TeX, los usuarios de PSTricks deben forzar pdfTeX al modo DVI o utilizar auto-pst-pdf. PGF/TikZ es una alternativa a PSTricks que es compatible con pdfTeX. Aplicaciones que soporta la generación de código PSTricks
Véase también
Bibliografía
http://assets.pearsonschool.com/asset_mgr/current/201033/VisualLearningResearch.pdf Enlaces externos
|
|||||||||||||||||||||||||||||||||||||||
