|
Método del codo (agrupamiento) En el análisis de conglomerados, el método del codo es un método que se utiliza para determinar el número de conglomerados en un conjunto de datos. El método consiste en graficar la variación explicada en función del número de conglomerados y elegir el codo de la curva como el número de conglomerados a utilizar. El mismo método se puede utilizar para elegir el número de parámetros en otros modelos basados en datos, como el número de componentes principales a usar para describir el conjunto de forma óptima. El método se remonta a las especulaciones de Robert L. Thorndike en 1953.[1] IntuiciónUtilizar el "codo" o la "rodilla de una curva" como punto de corte es un método común en la optimización matemática para elegir aquel punto a partir del cual los rendimientos decrecientes ya no justifican el costo adicional. En la agrupación en clústeres, esto significa que uno debe elegir una cantidad de clústeres de modo que agregar otro clúster no proporcione un modelado mucho mejor de los datos. La intuición es que aumentar el número de grupos mejorará naturalmente el ajuste (explicará más de la variación) ya que hay más parámetros (grupos) para usar, pero que en algún punto esto es un sobreajuste; esto es lo que el codo refleja. Por ejemplo, dados unos datos que consisten en k grupos etiquetados (por ejemplo, generados por k puntos muestreados con ruido), la agrupación en más de k grupos "explicará" una mayor parte de la variación (ya que puede usar grupos más pequeños y ajustados), pero esto es sobreajuste, ya que está subdividiendo los grupos etiquetados en múltiples grupos. La idea es que los primeros grupos agregarán mucha información (explicarán mucha variación) ya que los datos en realidad consisten en esa cantidad de grupos (siendo así estos grupos son necesarios), pero una vez que el número de grupos excede el número real de grupos en los datos, la información agregada caerá drásticamente porque solo estaremos subdividiendo los grupos reales. Suponiendo que esto suceda, habrá un codo pronunciado en el gráfico de la variación explicada frente al número de conglomerados: aumentando rápidamente hasta k (región de subajuste ), y luego aumentando lentamente después de k (región de sobreajuste). CríticaEl método del codo se considera subjetivo y poco fiable. En muchas aplicaciones prácticas, la elección de un "codo" es muy ambigua ya que la gráfica no contiene un codo pronunciado.[2] Esto puede incluso ser válido en casos en que todos los demás métodos para determinar el número de clústeres en un conjunto de datos coinciden en el número de clústeres óptimo. 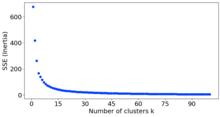 Incluso en datos aleatorios uniformes (sin grupos significativos) la curva sigue aproximadamente la relación 1/k donde k es el parámetro para el número de grupos, lo que hace que aparezca un "codo" y se pueda llegar a elegir erróneamente algún número "óptimo" de grupos.[3] Debido a que ambos ejes (el número de grupos y la varianza restante o la explicada) no tienen relación semántica, distintos intentos de capturar el codo mediante la "pendiente" están mal definidos y son sensibles al rango de parámetros.[3] Aumentar el número máximo de grupos puede cambiar la ubicación del "codo" que se percibe y, en muchos casos, métodos alternativos como el criterio de la razón de varianzas o el del ancho promedio de la silueta son más confiables.[3] Pero incluso con estas medidas, los resultados pueden depender mucho del preprocesamiento de los datos (selección de características y escalamiento) y los usuarios pueden llegar a resultados de agrupamiento muy diferentes con los mismos datos. Medidas de variaciónHay varias medidas de la "variación explicada" utilizadas en el método del codo. Lo más común es que la variación se cuantifique mediante la varianza, y la relación utilizada es la razón de la varianza entre grupos y la varianza total. Como alternativa, se utiliza la razón entre la varianza entre grupos y la varianza dentro del grupo, que es el estadístico para la prueba F de ANOVA de una vía.[4] Referencias
|