|
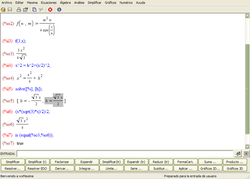
Maxima
El sistema de álgebra computacional Maxima es un motor de cálculo simbólico escrito en lenguaje Lisp publicado bajo licencia GNU GPL. Cuenta con un amplio conjunto de funciones para hacer manipulación simbólica de polinomios, matrices, funciones racionales, integración, derivación, manejo de gráficos en 2D y 3D, manejo de números de coma flotante muy grandes, expansión en series de potencias y de Fourier, entre otras funcionalidades. Además tiene un depurador a nivel de fuente para el código de Maxima. Maxima está basado en el sistema original de Macsyma desarrollado por MIT en los años 70. Es bastante fiable, tiene un buen recolector de basura, por lo que no desperdicia memoria. Viene con cientos de auto pruebas (test-suite). Maxima funciona en modo consola, sin embargo incluye las intefaces gráficas xMaxima y wxMaxima para facilitar su uso. El editor de texto científico GNU TeXmacs también puede ser usado para facilitar una interfaz gráfica de usuario para Maxima. Otras opciones son, imaxima, y el modo interactivo de Emacs. También puede hacer uso de la interfaz gráfica de SageMath, que facilita su integración con otras herramientas CAS. Como está escrito en Common Lisp, es fácilmente accesible para la programación, desde la capa inferior de Lisp puede llamarse a Maxima. Cálculo numéricoComo la mayoría de sistemas algebraicos, Maxima se especializa en operaciones simbólicas. También ofrece capacidades numéricas especiales, como son los números enteros y racionales, los cuales pueden crecer en tamaño solo limitado por la memoria de la máquina; y números reales en coma flotante, cuya precisión puede ser arbitrariamente larga (bfloat). Permite el manejo de expresiones simbólicas y numéricas, y además produce resultados con una alta precisión. Para cálculos intensivos en reales de coma flotante, Maxima ofrece la posibilidad de generar código en otros lenguajes de programación, como Fortran, que quizá se ejecuten de manera más eficiente. Maxima es un sistema de propósito general; como tal los cálculos especiales como la factorización de números grandes, la manipulación de polinomios extremadamente grandes, etc. son normalmente realizados de forma más eficiente y rápida en sistemas especializados. AlternativasSoftware libreSoftware privativoVéase tambiénEnlaces externos
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||