|
Lógica aristotélica La lógica aristotélica es la lógica basada en los trabajos del filósofo griego Aristóteles, quien es ampliamente reconocido como el padre fundador de la lógica.[1] Sus trabajos principales sobre la materia tradicionalmente se agrupan bajo el nombre Órganon («herramienta») y constituyen la primera investigación sistemática sobre los principios del razonamiento válido o correcto. Inició lo que se denomina como lógica de términos.[2][3] Para Aristóteles, la lógica era una herramienta necesaria para adentrarse en el mundo de la filosofía y la ciencia. Su lógica está a su vez vinculada con su metafísica.[4] Sus propuestas ejercieron una influencia sin par durante más de dos milenios,[1] a tal punto que en el siglo XVIII, Immanuel Kant llegó a afirmar:
El trabajo de Aristóteles se consideraba desde los tiempos clásicos, y particularmente durante la época medieval en Europa y el Medio Oriente, como la imagen misma de un sistema completamente elaborado. Sin embargo no estaba solo: los estoicos propusieron un sistema de lógica proposicional que fue estudiado por los lógicos medievales. También se estudió el problema de la generalidad múltiple. No obstante, no se consideraba que los problemas de la lógica aristotélica, tuvieran que necesitar soluciones revolucionarias. En la actualidad, algunos académicos afirman que el sistema de Aristóteles no puede aportar mucho más que valor histórico, debido a la llegada de la lógica matemática. Sin embargo, la lógica de Aristóteles se emplea, entre otros campos de estudio e investigación, en la teoría de la argumentación para ayudar a desarrollar y cuestionar críticamente los esquemas de argumentación que se utilizan en la inteligencia artificial y los argumentos legales. Axiomas Antes de embarcarse en este estudio de la sustancia, Aristóteles aborda los principios más fundamentales del razonamiento. Aristóteles los llama «axiomas» (en griego: axioein, "considerar digno"), los requisitos previos de toda argumentación y hasta de toda acción.[5] La rama de la lógica clásica, fundada por Aristóteles, tiene estos tres axiomas:[6][7]
La primera filosofía también debe ocuparse del principio de no contradicción: el principio de que "el mismo atributo no puede pertenecer al mismo tiempo y no debe pertenecer al mismo sujeto y al mismo respecto".[8][9] Aristóteles dice que este principio es el más seguro de todos los principios, y no es solo una hipótesis. Sin embargo, no puede probarse, ya que está empleado, implícitamente, en todas las pruebas, por lo que cualquier supuesta prueba sería circular. Aristóteles no argumenta que es una verdad necesaria, en cambio, que es imposible no creer en él.[10] Según Aristóteles, todo lo que es sensato, descansa en el principio de no contradicción. El buen juicio es consistente. Aristóteles señaló dos tipos de inconsistencias: la contradicción (antifásis), que ocurre cuando se afirma algo y lo contrario (ej: X es blanco y X no es blanco); y los contrarios, que son dos juicios que no pueden ser ambos ciertos pero sí los dos falsos (ej: X es blanco y X es negro).[11][12][13] JuiciosSegún Aristóteles, los argumentos o silogismos se componen de juicios (o proposiciones, apophanseis). Los juicios son oraciones con un sujeto (hipokeimenon) y un predicado (katêgorein), en las cuales el predicado se afirma o se niega del sujeto.[14][15] Así por ejemplo, «Sócrates es hombre» y «todos los hombres son mortales» son juicios. En la actualidad hablaríamos de proposiciones; pero se mantiene la denominación de juicio por ser más acorde con la filosofía de Aristóteles. Hoy se considera como juicio de términos considerando que cada término significa una propiedad como una clase lógica. Aristóteles llama término (horos) a aquello que puede ser sujeto o predicado de un juicio, y distingue entre términos singulares («Sócrates», «Platón») y términos universales («hombre», «mortal»).[13] Los términos singulares solo pueden ser sujeto, mientras que los términos universales pueden ser tanto sujeto como predicado (con ayuda de cuantificadores).[13] Siguiendo estos criterios, Aristóteles clasificó distintos tipos de juicios y también construyó el cuadro de oposición de los juicios. La siguiente tabla resume los tres tipos de juicios afirmativos y negativos: el universal (katholou, kata pantos), el particular (kata meros, en merei) o el indefinido (adihoristos).[13]
Silogismos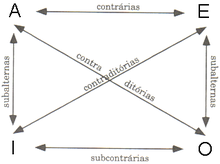 - A = Universal afirmativo. Término Sujeto tomado en su extensión universal; término Predicado particular; cualidad afirmativa (Todo S es P). - E = Universal negativo. Término Sujeto tomado en su extensión universal; término Predicado universal; cualidad negativa (Ningún S es P). - I = Particular afirmativo. Término Sujeto tomado en su extensión particular; término Predicado en su extensión particular; cualidad afirmativa (Algún S es P). - O = Particular negativo. Término Sujeto tomado en su extensión particular; término Predicado en su extensión universal; cualidad negativa (Algún S no es P). Según Aristóteles, toda proposición (apophansis) se compone de dos términos (horos), un sujeto (hipokeimenon) y un predicado (katêgorein); y puede ser verdadera o falsa.[2] Luego, todo enunciado afirmativo simple, puede reducirse a "S es P".[14] La noción central del sistema lógico de Aristóteles es el silogismo (o deducción, apódeixis o sullogismos).[16][17] Un silogismo es, según la definición de Aristóteles, «un discurso (logos) en el cual, establecidas ciertas cosas, resulta necesariamente de ellas, por ser lo que son, otra cosa diferente».[18] El silogismo es una inferencia en la que una conclusión (sumperasma) se sigue necesariamente de otras dos proposiciones, las "premisas" (protasis).[14] Un ejemplo clásico de silogismo es el siguiente:
En este ejemplo, tras establecer las premisas (1) y (2), la conclusión (3) se sigue por necesidad. La noción de silogismo es similar a la noción moderna de argumento deductivamente válido, pero hay diferencias.[19] En los Primeros analíticos, Aristóteles construyó la primera teoría de la inferencia válida.[20] Conocida como la silogística, la teoría ofrece criterios para evaluar la validez de ciertos tipos muy específicos de silogismos: los silogismos categóricos.[20] Para definir lo que es un silogismo categórico, primero es necesario definir lo que es una proposición categórica. Toda proposición contiene dos términos: un sujeto (S) y un predicado (P). Una proposición es categórica si tiene alguna de las siguientes cuatro formas:
A partir de estos cuatro ejes, Aristóteles en su obra Sobre la interpretación muestra un cuadro de oposición de los juicios (ver imagen de la derecha), donde se relaciona los valores de verdad entre cada jucio categórico. De ellos surgen jucios contrarios (A-E ), subcontrarios (I-O), contradictorios (A-O e I-E) y subalternos (A-I e E-O).[21] Un silogismo es categórico si está compuesto por exactamente tres proposiciones categóricas (dos premisas y una conclusión), y si ambas premisas comparten exactamente un término (llamado el término medio), que además no está presente en la conclusión. Por ejemplo, el silogismo mencionado más arriba es un silogismo categórico. Dadas estas definiciones, existen tres maneras en que el término medio puede estar distribuido entre las premisas. Sean A, B y C tres términos distintos, luego:
Aristóteles llama a estas tres posibilidades figuras.[22] El silogismo mencionado más arriba es una instancia de la primera figura. Dado que cada silogismo categórico consta de tres proposiciones categóricas, y que existen cuatro tipos de proposiciones categóricas, y tres tipos de figuras, existen 4 × 4 × 4 × 3 = 192 silogismos categóricos distintos. Algunos de estos silogismos son válidos, otros no. Para distinguir unos de otros, Aristóteles parte de dos silogismos categóricos que asume como válidos (algo análogo a las actuales reglas de inferencia), y demuestra a partir de ellos (con ayuda de tres reglas de conversión), la validez de todos y solo los silogismos categóricos válidos.[20] CategoríasEsta sección es un extracto de Categoría § Aristóteles.[editar] Aristóteles fue quizás el primer filósofo en abordar el estudio sistemático de las categorías escribiendo un libro sobre ellas. Su enfoque en líneas generales es materialista y concibe las categorías como reflejo de las propiedades generales de los fenómenos objetivos. Presenta su lista de las diez categorías en Tópicos I.9, 103b20-25 y Categorías, IV, 1 b 25-27.[23][24] Las diez categorías se pueden interpretar de tres maneras diferentes: como tipos de predicados, como clasificación de los sermones o como tipos de entidades.
Existe la hipótesis de que Aristóteles consideraba las categorías de posesión y situación como sub-categorías, subsumibles quizás en héxis y diáthesis respectivamente, dos sub-clases de cualidad.[25] Otras nociones se encuentran Accidente «[Lo que] está en un sujeto, pero no se dice de ningún sujeto […]; [y lo que] se dice de un sujeto y está en un sujeto» y Sustancia segunda.[24] Este listado aparece también en otras obras, omitiéndose algunas categorías, come en Tópicos, I, 9, 103 b 20-23; Metafísica, V, 7, 1017 a 25; Segundos analíticos, I, 22, 83 a 21-22 y en Física, V, 1, 225 b 6-8. La categoría más importante es la sustancia o entidad, habiendo dos tipos, la entidad concreta o primera y abstracta o segunda.[26] En cierto modo, la entidad concreta no es una categoría porque no se puede predicar.[27] Entonces, aun sabiendo uno por definición qué es una cosa, no sabrá si es o si existe, pues el ser no es ningún género ni entidad de nada. En esto punto se diferencia mejor la ontología aristotélica de la platónica.[28] El tratado aristotélico de las Categorías ha sido ampliamente discutida por los comentadores de Aristóteles desde la Antigüedad, como Simplicio, Olimpiodoro, Tomás de Aquino y Giulio Pace.[24] Fue objeto de un gran número de críticas. Kant objetó que están enumeradas al azar y no son deducidas de un principio general (véase Categoría de Kant). Otro reproche recibido fue incluir la substancia como categoría del ser cuando la substancia es el ser mismo.[29] Para Jesús Mosterín, la teoría aristotélica de las categorías es muy oscura porque no se sabe bien cuando Aristóteles habla de cosas o de nociones y ni justifica porque son esas y no otras.[30]Otros aportesAdemás de su teoría de los silogismos, Aristóteles realizó una gran cantidad de otros aportes a la lógica. En Sobre la interpretación se encuentran algunas observaciones y propuestas de lógica modal, así como una controversial e influyente discusión acerca de la relación entre el tiempo y la necesidad.[31][32] Según Aristóteles, del par de proposiciones «mañana habrá una batalla naval» y «mañana no habrá una batalla naval», parece que alguna tiene que ser verdadera hoy y la otra falsa. Supongamos que la primera fuera verdadera hoy. Luego, mañana habrá una batalla naval. Pero entonces el futuro ya está determinado, y no depende de nosotros. Lo mismo sucede si suponemos que la segunda proposición es verdadera hoy. Sin embargo, nos parece que el futuro no está determinado, y que en algún sentido importante sí depende de nosotros. Frente a esta situación, Aristóteles discute la posibilidad de que las proposiciones acerca del futuro no sean ni verdaderas ni falsas, es decir una lógica plurivalente. Aristóteles también reconoció la existencia e importancia de los argumentos inductivos, en los cuales se va «de lo particular a lo universal», pero dedicó poco espacio a su estudio.[33] Por si fuera poco, Aristóteles fue el primero en realizar un estudio sistemático de las falacias. En sus Refutaciones sofísticas identificó y clasificó trece tipos de falacias,[34] entre ellas la afirmación del consecuente, la petición de principio y la conclusión irrelevante. RecepciónSe considera a Aristóteles el fundador de la lógica como propedéutica o herramienta básica para todas las ciencias. La lógica aristotélica fue ampliamente aceptada en ciencias y matemáticas y permaneció en uso amplio en Occidente. El sistema de lógica de Aristóteles fue responsable de la introducción del silogismo hipotético, de la lógica modal temporal, de la lógica inductiva, así como de términos influyentes tales como términos, predicables, silogismos y proposiciones. En Europa durante el último período de la época medieval, se hicieron grandes esfuerzos para demostrar que las ideas de Aristóteles eran compatibles con la fe cristiana. Durante la Alta Edad Media, la lógica se convirtió en el foco principal de los filósofos, que participarían en análisis lógicos críticos de los argumentos filosóficos, a menudo utilizando variaciones de la metodología del escolasticismo. A través del latín en Europa occidental y de distintas lenguas orientales como el árabe, armenio y georgiano, la tradición aristotélica fue considerada de forma especial para la codificación de las leyes del razonamiento. La lógica aristotélica y estóica mantuvo siempre una relación con los argumentos formulados en lenguaje natural. Por eso aunque eran formales, no eran formalistas. Hoy esa relación se trata bajo un punto de vista completamente diferente. La formalización estricta ha mostrado las limitaciones de la lógica tradicional o aristotélica, que hoy se interpreta como una parte pequeña de la lógica de clases. Ayn Rand declaró que consideraba a Aristóteles como el mayor filósofo del mundo y apreciaba en especial su Órganon ('Lógica').[35] Según Lenin: "La lógica de Aristóteles es una interrogación, una búsqueda, un acceso a la lógica de Hegel".[4] A finales del siglo XIX se descubría como insuficiente el análisis lógico de Aristóteles.[14] Este enfoque cambió cuando Gottlob Frege desarrolló nociones de cuantificación y predicación en su lógica, haciendo obsoleto el silogismo.[36] CríticasBertrand Russell en su libro Historia de la filosofía occidental fue muy crítico con la lógica de Aristóteles y lo expresa en tres puntos:[37]
Además, Russell termina su revisión de la lógica aristotélica con estas palabras:
Véase tambiénNotas y referencias
Bibliografía adicional
Enlaces externos
|
|||||||||||||||||||||||||||||||||||||||||||||||


