Envolvente (ondas)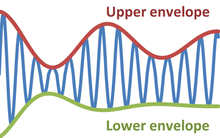

Funciones de envolvente superior e inferior para una onda sinusoidal modulada.

En física e ingeniería, la envolvente de una señal oscilante es una curva suave que describe sus extremos. Así, la envolvente generaliza el concepto de amplitud constante en amplitud instantánea. La figura ilustra una onda sinusoidal modulada que varía entre una envolvente superior e inferior. La función de la envolvente puede ser función del tiempo, espacio, ángulo o incluso de cualquier variable.

Ejemplo: ondas pulsantes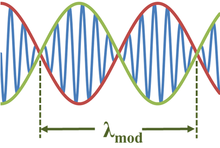

Onda modulada resultante de la adición de dos ondas sinusoidales de longitud de onda y frecuencia casi idénticas.

Una situación común que da como resultado una función envolvente tanto en el espacio x como en el tiempo t es la superposición de dos ondas de casi la misma longitud de onda y frecuencia:[1]​

${\displaystyle {\begin{aligned}F(x,\ t)&=\sin \left[2\pi \left({\frac {x}{\lambda -\Delta \lambda }}-(f+\Delta f)t\right)\right]+\sin \left[2\pi \left({\frac {x}{\lambda +\Delta \lambda }}-(f-\Delta f)t\right)\right]\\[6pt]&\approx 2\cos \left[2\pi \left({\frac {x}{\lambda _{\rm {mod}}}}-\Delta f\ t\right)\right]\ \sin \left[2\pi \left({\frac {x}{\lambda }}-f\ t\right)\right]\end{aligned}}}$

que usa la fórmula trigonométrica para la suma de dos ondas sinusoidales, y la aproximación Δ λ ≪ λ:

${\displaystyle {\frac {1}{\lambda \pm \Delta \lambda }}={\frac {1}{\lambda }}\ {\frac {1}{1\pm \Delta \lambda /\lambda }}\approx {\frac {1}{\lambda }}\mp {\frac {\Delta \lambda }{\lambda ^{2}}}.}$

Aquí la longitud de onda de modulación λ_mod viene dada por:[1]​[2]​

${\displaystyle \lambda _{\rm {mod}}={\frac {\lambda ^{2}}{\Delta \lambda }}\ .}$

La longitud de onda de modulación es el doble que la de la propia envolvente porque cada media longitud de onda de la onda cosenoidal moduladora gobierna los valores positivos y negativos de la onda sinusoidal modulada. Asimismo, la frecuencia de batido es la de la envolvente, el doble que la de la onda moduladora, o 2Δ f .

Si esta onda es una onda de sonido, el oído escucha la frecuencia asociada con f y la amplitud de este sonido varía con la frecuencia del pulso.

Velocidad de fase y grupo

El cuadrado rojo se mueve con la velocidad de fase y los círculos verdes se propagan con la velocidad de grupo.

El argumento de las sinusoides anteriores además de un factor 2π son:

${\displaystyle \xi _{C}=\left({\frac {x}{\lambda }}-f\ t\right)\ ,}$

${\displaystyle \xi _{E}=\left({\frac {x}{\lambda _{\rm {mod}}}}-\Delta f\ t\right)\ ,}$

con los subíndices C y E que se refieren al transportista y a la envolvente. La misma amplitud F de la onda resulta de los mismos valores de ξ _C y ξ _E, cada uno de los cuales puede volver al mismo valor sobre elecciones diferentes pero adecuadamente relacionadas de x y t . Esta invariancia significa que uno puede rastrear estas formas de onda en el espacio para encontrar la velocidad de una posición de amplitud fija a medida que se propaga en el tiempo; para que el argumento de la onda portadora permanezca igual, la condición es:

${\displaystyle \left({\frac {x}{\lambda }}-f\ t\right)=\left({\frac {x+\Delta x}{\lambda }}-f(t+\Delta t)\right)\ ,}$

que muestra que para mantener una amplitud constante la distancia Δ x está relacionada con el intervalo de tiempo Δ t por la llamada velocidad de fase v _p

${\displaystyle v_{\rm {p}}={\frac {\Delta x}{\Delta t}}=\lambda f\ .}$

Por otro lado, las mismas consideraciones muestran que la envolvente se propaga a la llamada velocidad de grupo v_g:

${\displaystyle v_{\rm {g}}={\frac {\Delta x}{\Delta t}}=\lambda _{\rm {mod}}\Delta f=\lambda ^{2}{\frac {\Delta f}{\Delta \lambda }}\ .}$

Una expresión más común para la velocidad del grupo se obtiene introduciendo el vector de onda k :

${\displaystyle k={\frac {2\pi }{\lambda }}\ .}$

Observamos que para pequeños cambios Δ λ, la magnitud del pequeño cambio correspondiente en el vector de onda, digamos Δ k, es:

${\displaystyle \Delta k=\left|{\frac {dk}{d\lambda }}\right|\Delta \lambda =2\pi {\frac {\Delta \lambda }{\lambda ^{2}}}\ ,}$

por lo que la velocidad del grupo se puede reescribir como:

${\displaystyle v_{\rm {g}}={\frac {2\pi \Delta f}{\Delta k}}={\frac {\Delta \omega }{\Delta k}}\ ,}$

donde ω es la frecuencia en radianes / s: ω = 2 π f . En todos los medios, la frecuencia y el vector de onda están relacionados por una relación de dispersión, ω = ω ( k ), y la velocidad del grupo se puede escribir:

${\displaystyle v_{\rm {g}}={\frac {d\omega (k)}{dk}}\ .}$

Relación de dispersión ω = ω ( k ) para algunas ondas correspondientes a vibraciones de rejilla en GaAs.

En un medio como el vacío clásico, la relación de dispersión de las ondas electromagnéticas es:

${\displaystyle \omega =c_{0}k}$

donde c ₀ es la velocidad de la luz en el vacío clásico. Para este caso, las velocidades de fase y de grupo son c₀.

En los llamados medios dispersivos, la relación de dispersión puede ser una función complicada del vector de onda, y las velocidades de fase y de grupo no son las mismas. Por ejemplo, para varios tipos de ondas exhibidas por vibraciones atómicas (fonones) en GaAs, las relaciones de dispersión se muestran en la figura para varias direcciones del vector de onda k. En el caso general, las velocidades de fase y de grupo pueden tener diferentes direcciones.

Ejemplo: aproximación de la función de envolvente

Probabilidades de electrones en los dos estados cuánticos más bajos de un pozo cuántico de 160Ǻ GaAs en una heteroestructura GaAs-GaAlAs calculada a partir de funciones de envolvente.

En física de la materia condensada, una función propia de energía para un portador de carga móvil en un cristal se puede expresar como una onda de Bloch:

${\displaystyle \psi _{n\mathbf {k} }(\mathbf {r} )=e^{i\mathbf {k} \cdot \mathbf {r} }u_{n\mathbf {k} }(\mathbf {r} )\ ,}$

donde n es el índice de la banda (por ejemplo, banda de conducción o de valencia) r es una ubicación espacial y k es un vector de onda. La exponencial es una función que varía sinusoidalmente correspondiente a una envolvente que se modifica lentamente y modula la parte que varía rápidamente de la función de onda u_n,k describiendo el comportamiento de la función de onda cerca de los núcleos de los átomos de la red. La envolvente está restringida a valores k dentro de un rango limitado por la zona de Brillouin del cristal, y eso limita la rapidez con la que puede variar con la ubicación r.

Para determinar el comportamiento de los portadores utilizando la mecánica cuántica, se suele utilizar la aproximación de la envolvente en la que la ecuación de Schrödinger se simplifica para referirse únicamente al comportamiento de la envolvente, y las condiciones de contorno se aplican a la función envolvente directamente, en lugar de a la completa. función de onda. Por ejemplo, la función de onda de un portador atrapado cerca de una impureza está gobernada por una función de envolvente F que gobierna una superposición de funciones de Bloch:

${\displaystyle \psi (\mathbf {r} )=\sum _{\mathbf {k} }F(\mathbf {k} )e^{i\mathbf {k\cdot r} }u_{\mathbf {k} }(\mathbf {r} )\ ,}$

donde los componentes de Fourier de la envolvente F(k) se encuentran a partir de la ecuación de Schrödinger aproximada. En algunas aplicaciones, la parte periódica u_k se reemplaza por su valor cerca del borde de la banda, digamos k = k₀, y luego:

${\displaystyle \psi (\mathbf {r} )\approx \left(\sum _{\mathbf {k} }F(\mathbf {k} )e^{i\mathbf {k\cdot r} }\right)u_{\mathbf {k} =\mathbf {k} _{0}}(\mathbf {r} )=F(\mathbf {r} )u_{\mathbf {k} =\mathbf {k} _{0}}(\mathbf {r} )\ .}$

Ejemplo: patrones de difracción

El patrón de difracción de una rendija doble tiene una envolvente de una sola rendija.

Los patrones de difracción de múltiples rendijas tienen envolventes determinadas por el patrón de difracción de una sola rendija. Para una sola hendidura, el patrón viene dado por:

${\displaystyle I_{1}=I_{0}\sin ^{2}\left({\frac {\pi d\sin \alpha }{\lambda }}\right)/\left({\frac {\pi d\sin \alpha }{\lambda }}\right)^{2}\ ,}$

donde α es el ángulo de difracción, d es el ancho de la rendija y λ es la longitud de onda. Para múltiples rendijas, el patrón es

${\displaystyle I_{q}=I_{1}\sin ^{2}\left({\frac {q\pi g\sin \alpha }{\lambda }}\right)/\sin ^{2}\left({\frac {\pi g\sin \alpha }{\lambda }}\right)\ ,}$

donde q es el número de rendijas yg es la constante de rejilla. El primer factor, el resultado de una sola rendija I ₁, modula el segundo factor de variación más rápida que depende del número de rendijas y su espaciamiento.

Véase también

• Envolvente compleja
• Descomposición en modo empírico
• Envolvente
• Detector de envolvente
• Modulación
• Matemáticas de oscilación
• Potencia máxima de la envolvente
• Envolvente espectral

Referencias

1. Blair Kinsman (2002). Wind Waves: Their Generation and Propagation on the Ocean Surface (Reprint of Prentice-Hall 1965 edición). Courier Dover Publications. p. 186. ISBN 0486495116. 
2. Mark W. Denny (1993). Air and Water: The Biology and Physics of Life's Media. Princeton University Press. pp. 289. ISBN 0691025185. 

• Datos: Q5380913