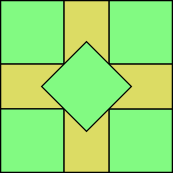
Empaquetado de cuadrados

El empaquetado de cuadrados es un problema de empaquetado donde el objetivo es determinar cuántos cuadrados congruentes se pueden empaquetar en una forma más grande, a menudo un cuadrado o un círculo.

Empaquetado de cuadrados en un cuadrado

Empaquetar cuadrados en un cuadrado es el problema de determinar el número máximo de cuadrados unidad (cuadrados de longitud de lado uno) que se pueden empaquetar dentro de un cuadrado más grande de longitud de lado ${\displaystyle a}$. Si ${\displaystyle a}$ es un número entero, la respuesta es ${\displaystyle a^{2},}$, pero la cantidad precisa (o incluso asintótica) del espacio que queda sin cubrir para un ${\displaystyle a}$ arbitrario no entero es una pregunta abierta.[1]​

5 cuadrados unitarios en un cuadrado de longitud de lado ${\displaystyle 2+1/{\sqrt {2}}\approx 2.707}$

10 cuadrados unitarios en un cuadrado de longitud de lado ${\displaystyle 3+1/{\sqrt {2}}\approx 3.707}$

11 cuadrados unitarios en un cuadrado de longitud de lado ${\displaystyle a\approx 3.877084}$

El valor más pequeño de ${\displaystyle a}$ que permite empaquetar cuadrados unitarios ${\displaystyle n}$ se conoce cuando ${\displaystyle n}$ es un cuadrado perfecto (en cuyo caso es ${\displaystyle {\sqrt {n}}}$), así como para ${\displaystyle n={}}$2, 3, 5, 6, 7, 8, 10, 13, 14, 15, 24, 34, 35, 46, 47 y 48. Para la mayoría de estos números (con la única excepción de 5 y 10), el empaquetamiento es el natural con cuadrados alineados con los ejes horizontal y vertical, y ${\displaystyle a}$ es ${\displaystyle \lceil {\sqrt {n}}\,\rceil }$, donde ${\displaystyle \lceil \,\ \rceil }$ donde ceiling es es la función redondeo hacia arriba.[2]​[3]​ La figura muestra los empaquetamientos óptimos para 5 y 10 cuadrados, los dos números más pequeños de cuadrados para los cuales el empaquetamiento óptimo involucra disponer cuadrados inclinados.[4]​[5]​

El caso más pequeño sin resolver implica empaquetar 11 cuadrados unitarios en un cuadrado más grande. No se pueden empaquetar 11 unidades de cuadrados en un cuadrado de longitud de lado menor que ${\displaystyle \textstyle 2+2{\sqrt {4/5}}\approx 3.789}$. Por el contrario, el empaquetamiento más apretado conocido de 11 cuadrados está dentro de un cuadrado de longitud de lado de aproximadamente 3,877084; solución encontrada por Walter Trump.[6]​[4]​

Resultados asintóticos

Problemas no resueltos de la matemática: ¿Cuál es la tasa de crecimiento asintótico del espacio desperdiciado al empaquetar cuadrados en un cuadrado de lado semientero?

Para valores mayores de la longitud del lado ${\displaystyle a}$, se desconoce el número exacto de cuadrados unitarios que pueden empaquetarse en un cuadrado de lado ${\displaystyle a\times a}$. Siempre es posible empaquetar una cuadrícula ${\displaystyle \lfloor a\rfloor \!\times \!\lfloor a\rfloor }$ de cuadrados unitarios alineados con el eje, pero esto puede dejar un área grande, aproximadamente ${\displaystyle 2a(a-\lfloor a\rfloor )}$, descubierta y desperdiciada.[4]​ En cambio, Paul Erdős y Ronald Graham demostraron que para un empaquetado diferente mediante cuadrados unitarios inclinados, el espacio desperdiciado podría reducirse significativamente a ${\displaystyle o(a^{7/11})}$ (aquí escrito como cota superior asintótica).[7]​ Posteriormente, Graham y Fan Chung redujeron aún más el espacio desperdiciado a ${\displaystyle O(a^{3/5})}$.[8]​ Sin embargo, como Klaus Roth y Bob Vaughan demostraron, todas las soluciones deben desperdiciar al menos un espacio de ${\displaystyle \Omega {\bigl (}a^{1/2}(a-\lfloor a\rfloor ){\bigr )}}$. En particular, cuando ${\displaystyle a}$ es un número semientero, el espacio desperdiciado es al menos proporcional a su raíz cuadrada.[9]​ La tasa de crecimiento asintótica precisa del espacio desperdiciado, incluso para longitudes de lados semienteros, sigue siendo un problema no resuelto.[1]​

Algunos números de cuadrados unitarios nunca son el número óptimo en un empaquetamiento. En particular, si un cuadrado de tamaño ${\displaystyle a\times a}$ permite empaquetar ${\displaystyle n^{2}-2}$ cuadrados unitarios, entonces debe darse el caso de que ${\displaystyle a\geq n}$, y que también es posible un empaquetamiento de cuadrados unitarios ${\displaystyle n^{2}}$.[2]​

Empaquetado de cuadrados en un círculo

Empaquetar cuadrados en un círculo es un problema relacionado con empaquetar n cuadrados unitarios en un círculo con un radio lo más pequeño posible. Para este problema, se conocen buenas soluciones para n hasta 35. A continuación se muestran las soluciones mínimas para n hasta 12:[10]​

Número de cuadrados	Radio del círculo
1	0.707...
2	1.118...
3	1.288...
4	1.414...
5	1.581...
6	1.688...
7	1.802...
8	1.978...
9	2.077...
10	2.121...
11	2.214...
12	2.236...

Véase también

• Empaquetado de círculos en un cuadrado
• Cuadratura del cuadrado
• Empaquetado de rectángulos
• Problema del sofá

Referencias

1. Brass, Peter; Moser, William; Pach, János (2005), Research Problems in Discrete Geometry, New York: Springer, p. 45, ISBN 978-0387-23815-9, LCCN 2005924022, MR 2163782 .
2. Kearney, Michael J.; Shiu, Peter (2002), «Efficient packing of unit squares in a square», Electronic Journal of Combinatorics 9 (1), Research Paper 14, 14 pp., MR 1912796 .
3. Bentz, Wolfram (2010), «Optimal packings of 13 and 46 unit squares in a square», The Electronic Journal of Combinatorics 17 (R126), MR 2729375, arXiv:1606.03746, doi:10.37236/398 .
4. Friedman, Erich (2009), «Packing unit squares in squares: a survey and new results», Electronic Journal of Combinatorics, Dynamic Survey 7, MR 1668055 .
5. Stromquist, Walter (2003), «Packing 10 or 11 unit squares in a square», Electronic Journal of Combinatorics 10, Research Paper 8, MR 2386538 .
6. Gensane, Thierry; Ryckelynck, Philippe (2005), «Improved dense packings of congruent squares in a square», Discrete & Computational Geometry 34 (1): 97-109, MR 2140885, doi:10.1007/s00454-004-1129-z .
7. Erdős, P.; Graham, R. L. (1975), «On packing squares with equal squares», Journal of Combinatorial Theory, Series A 19: 119-123, MR 0370368, doi:10.1016/0097-3165(75)90099-0 .
8. Chung, Fan; Graham, Ron (2020), «Efficient packings of unit squares in a large square», Discrete & Computational Geometry 64 (3): 690-699, doi:10.1007/s00454-019-00088-9 .
9. Roth, K. F.; Vaughan, R. C. (1978), «Inefficiency in packing squares with unit squares», Journal of Combinatorial Theory, Series A 24 (2): 170-186, MR 0487806, doi:10.1016/0097-3165(78)90005-5 .
10. Friedman, Erich, Squares in Circles .

Enlaces externos

• Friedman, Erich, «Squares in Squares», Github, Erich's Packing Center .

• Datos: Q7582076