Determinación de constantes de equilibrio

Equilibrios químicos
Equilibros
Equilibrio químico Estabilidad química Equilibrio dinámico Equilibrio de solubilidad Equilibrio termodinámico Equilibrio vapor-líquido
Constantes
Constante de disociación ácida Constante de unión Constante de disociación Coeficiente de partición Constante de equilibrio Cociente de reacción Constantes de estabilidad de complejos Selectividad de unión Actividad termodinámica
Conceptos
Solución tampón Quelación Determinación de constantes de equilibrio Química del equilibrio Desarrollo de equilibrio Etapa de equilibrio Función de acidez de Hammett Ley de Henry Extracción líquido-líquido Efecto macrociclo Diagrama de fases Diagrama de predominio Regla de fase Autoionización del agua

Las constantes de equilibrio se determinan para cuantificar los equilibrios químicos. Cuando una constante de equilibrio K se expresa como un cociente de concentración,

${\displaystyle K={\frac {\mathrm {[S]} ^{\sigma }\mathrm {[T]} ^{\tau }\cdots }{\mathrm {[A]} ^{\alpha }\mathrm {[B]} ^{\beta }\cdots }}}$

se implica que el cociente de actividad es constante. Para que esta suposición sea válida, las constantes de equilibrio deben determinarse en un medio de fuerza iónica relativamente alta. Cuando esto no sea posible, se debe considerar la posible variación de la actividad.

La expresión de equilibrio anterior es una función de las concentraciones [A], [B], etc. de la especie química en equilibrio. El valor constante de equilibrio puede determinarse si se puede medir cualquiera de estas concentraciones. El procedimiento general es que la concentración en cuestión se mide para una serie de soluciones con concentraciones analíticas conocidas de los reactivos. Típicamente, una titulación se realiza con uno o más reactivos en el recipiente de titulación y uno o más reactivos en la bureta. Al conocer las concentraciones analíticas de los reactivos inicialmente en el recipiente de reacción y en la bureta, todas las concentraciones analíticas se pueden derivar en función del volumen (o masa) del valorante agregado.

Las constantes de equilibrio pueden derivarse ajustando mejor los datos experimentales con un modelo químico del sistema de equilibrio.

Métodos experimentales

Hay cuatro métodos experimentales principales.[1]​

Mediciones potenciométricas

Una concentración libre [A] o actividad {A} de una especie A se mide por medio de un electrodo selectivo de iones como el electrodo de vidrio. Si el electrodo se calibra utilizando estándares de actividad, se supone que la ecuación de Nernst se aplica en la forma

${\displaystyle E=E^{0}+{\frac {RT}{nF}}\ln \mathrm {\{A\}} }$

donde E^0 es el potencial de electrodo estándar. Cuando se utilizan soluciones tampón de pH conocido para la calibración, la lectura del medidor será un pH.

${\displaystyle \mathrm {pH} ={\frac {nF}{RT}}\left(E^{0}-E\right)}$

A los 298 K,1 la unidad de pH es aproximadamente igual a 59 mV.[2]​

Cuando el electrodo se calibra con soluciones de concentración conocida, por medio de una fuerte titulación ácido-fuerte, por ejemplo, se supone una ecuación de Nernst modificada.

${\displaystyle E=E^{0}+s\log _{10}\mathrm {[A]} }$

donde s es un factor de pendiente empírico. Se puede preparar una solución de concentración conocida de iones de hidrógeno mediante la estandarización de un ácido fuerte contra el bórax. El ácido clorhídrico de ebullición constante también se puede usar como un estándar primario para la concentración de iones de hidrógeno.

Mediciones espectrofotométricas

Absorbancia

Se supone que se aplica la ley de Beer-Lambert.

${\displaystyle A=l\sum {\varepsilon c}}$

donde l es la longitud del camino óptico, ε es una absorbancia molar a la longitud del camino unitario y c es una concentración. Más de una de las especies puede contribuir a la absorbancia. En principio, la absorbancia se puede medir solo en una longitud de onda, pero en la práctica actual es común registrar espectros completos.

Fluorescencia (luminiscencia) intensidad

Se supone que la intensidad de la luz dispersada es una función lineal de las concentraciones de las especies.

${\displaystyle I=\sum \varphi c}$

donde φ es una constante de proporcionalidad.

Mediciones de desplazamiento químico de RMN

Se supone que el intercambio químico es rápido en la escala de tiempo de RMN. Un cambio químico individual ${\displaystyle {\bar {\delta }}}$ es el promedio ponderado en fracciones molares de los cambios ${\displaystyle \delta }$ de núcleos en las especies contribuyentes.

${\displaystyle {\bar {\delta }}={\frac {\sum x_{i}\delta _{i}}{\sum x_{i}}}}$

Ejemplo: la pK_a del grupo hidroxilo en el ácido cítrico se determinó a partir de los datos de cambio químico del ^13C como 14.4. Para esta determinación no se pudo utilizar potenciometría ni espectrofotometría UV visible.[3]​

Mediciones calorimétricas

La medición simultánea de K y ΔH para aductos 1:1 se realiza de forma rutinaria mediante calorimetría de titulación isotérmica. La extensión a sistemas más complejos está limitada por la disponibilidad de software adecuado.

Rango y limitaciones

Potenciometría

El electrodo más utilizado es el electrodo de vidrio, que es selectivo para el ion hidrógeno. Esto es adecuado para todos los equilibrios ácido-base. log₁₀ β valores log₁₀ β entre aproximadamente 2 y 11 se pueden medir directamente mediante valoración potenciométrica utilizando un electrodo de vidrio. Este enorme rango es posible debido a la respuesta logarítmica del electrodo. Las limitaciones surgen porque la ecuación de Nernst se descompone a un pH muy bajo o muy alto. El rango se puede ampliar utilizando el método de competición. Un ejemplo de la aplicación de este método se puede encontrar en el cianuro de paladio (II).
Cuando se usa un electrodo de vidrio para obtener las mediciones de las que dependen las constantes de equilibrio calculadas, la precisión de los parámetros calculados está limitada por efectos secundarios tales como la variación de los potenciales de unión líquida en el electrodo. En la práctica, es prácticamente imposible obtener una precisión para log β mejor que ± 0.001.

Absorbancia y luminiscencia

Generalmente se cita un límite superior en el log₁₀ β de 4, que corresponde a la precisión de las mediciones, pero también depende de la intensidad del efecto. Los espectros de las especies contribuyentes deben ser claramente distintos entre sí.

RMN

La precisión limitada de las mediciones de desplazamiento químico también pone un límite superior de aproximadamente 4 en log₁₀ β. Limitado a los sistemas diamagnéticos. ^1HRMN no se puede utilizar con soluciones de compuestos en ^1H₂O.

Calorimetría

Actualmente no se dispone de pruebas suficientes.

Métodos computacionales

Se supone que los datos experimentales recopilados comprenden un conjunto de puntos de datos. En cada i punto de datos, las concentraciones analíticas de los reactivos, T_A(i) T_B(i) etc son conocidos junto con una cantidad medida, y_i que depende de uno o más de estas concentraciones analíticas. Un procedimiento computacional general tiene cuatro componentes principales:

1. Definición de un modelo químico de los equilibrios.
2. Cálculo de las concentraciones de todas las especies químicas en cada solución.
3. Refinamiento de las constantes de equilibrio.
4. Selección de modelo

El modelo químico

El modelo químico consiste en un conjunto de especies químicas presentes en solución, tanto los reactivos agregados a la mezcla de reacción como las especies complejas formadas a partir de ellos. Denotando los reactivos por A, B..., cada especie compleja está especificada por los coeficientes estequiométricos que relacionan la combinación particular de reactivos que los forman.

${\displaystyle {\ce {{{\mathit {p}}A}+{\mathit {q}}B\cdots <=>A_{\mathit {p}}B_{\mathit {q}}\cdots }}}$: ${\displaystyle \beta _{pq\cdots }={\frac {[{\ce {A}}_{p}{\ce {B}}_{q}\cdots ]}{[{\ce {A}}]^{p}[{\ce {B}}]^{q}\cdots }}}$

Cuando se usan programas de computadora de propósito general, es usual usar constantes de asociación acumulativas, como se muestra arriba. Las cargas eléctricas no se muestran en expresiones generales como esta y, a menudo, se omiten en expresiones específicas, por simplicidad de notación. De hecho, las cargas eléctricas no tienen relación con los procesos de equilibrio, salvo que existe un requisito de neutralidad eléctrica general en todos los sistemas.

Con las soluciones acuosas, las concentraciones de protón (ion hidronio) e ion hidróxido están limitadas por la autodisociación del agua.

${\displaystyle {\ce {H2O <=> H+ + OH-}}}$: ${\displaystyle K_{\mathrm {W} }^{'}={\frac {[H^{+}][OH^{-}]}{[H_{2}O]}}}$

Con las soluciones diluidas, la concentración de agua se supone constante, por lo que la expresión de equilibrio se escribe en forma del producto iónico del agua.

${\displaystyle K_{\mathrm {W} }={\ce {[H+]}}[{\ce {OH-}}]\,}$

Cuando tanto H ^+ como OH ^- deben considerarse reactivos, uno de ellos se elimina del modelo especificando que su concentración se deriva de la concentración del otro. Normalmente la concentración del ion hidróxido viene dada por

${\displaystyle [{\ce {OH-}}]={\frac {K_{{\ce {W}}}}{[{\ce {H+}}]}}\,}$

En este caso, la constante de equilibrio para la formación de hidróxido tiene los coeficientes estequiométricos -1 en relación con el protón y cero para los otros reactivos. Esto tiene implicaciones importantes para todos los equilibrios de protonación en solución acuosa y en particular para las constantes de hidrólisis.

Es bastante habitual omitir en el modelo aquellas especies cuyas concentraciones se consideran insignificantes. Por ejemplo, generalmente se asume que no hay interacción entre los reactivos y / o complejos y el electrolito usado para mantener la fuerza iónica constante o el tampón usado para mantener el pH constante. Estas suposiciones pueden o no estar justificadas. Además, se asume implícitamente que no hay otras especies complejas presentes. Cuando los complejos se ignoran erróneamente, se introduce un error sistemático en los cálculos.

Los valores constantes de equilibrio generalmente se estiman inicialmente por referencia a las fuentes de datos.

Cálculos de especiación

Un cálculo de especiación es uno en el que se calculan las concentraciones de todas las especies en un sistema de equilibrio, conociendo las concentraciones analíticas, T_A, T_B, etc., de los reactivos A, B, etc. Esto significa resolver un conjunto de ecuaciones no lineales de balance de masa.

${\displaystyle {\begin{aligned}{\ce {T_{A}}}&=[{\ce {A}}]+\sum _{1,nk}p\beta _{pq\cdots }[{\ce {A}}]^{p}[{\ce {B}}]^{q}\cdots \\{\ce {T_{B}}}&=[{\ce {B}}]+\sum _{1,nk}q\beta _{pq\cdots }[{\ce {A}}]^{p}[{\ce {B}}]^{q}\cdots \\etc.\end{aligned}}}$

para las concentraciones libres [A], [B] etc. Cuando se mide el pH (o emf, E) equivalente, la concentración libre de iones de hidrógeno, [H], se obtiene del valor medido como

${\displaystyle [\mathrm {H} ]=10^{-\mathrm {pH} }}$ or ${\displaystyle [\mathrm {H} ]=10^{\mathrm {\frac {E-E^{0}}{2.303RT/nF}} }}$

y solo se calculan las concentraciones libres de los otros reactivos. Las concentraciones de los complejos se derivan de las concentraciones libres a través del modelo químico.

Algunos autores[4]​[5]​ incluyen los términos reactivos libres en las sumas al declarar constantes β identidad (unidad) para las cuales los coeficientes estequiométricos son 1 para el reactivo en cuestión y cero para todos los demás reactivos. Por ejemplo, con 2 reactivos, las ecuaciones de balance de masa toman la forma más simple.

${\displaystyle {\begin{aligned}T_{\ce {A}}&=\sum _{0,nk}p\beta _{pq}[{\ce {A}}]^{p}[{\ce {B}}]^{q}\\[4pt]T_{\ce {B}}&=\sum _{0,nk}q\beta _{pq}[{\ce {A}}]^{p}[{\ce {B}}]^{q}\\\end{aligned}}}$

${\displaystyle \beta _{10}=\beta _{01}=1}$

De esta manera, todas las especies químicas, incluidos los reactantes libres, se tratan de la misma manera, ya que se han formado a partir de la combinación de reactivos que se especifica mediante los coeficientes estequiométricos.

En un sistema de titulación, las concentraciones analíticas de los reactivos en cada punto de titulación se obtienen de las condiciones iniciales, las concentraciones de bureta y los volúmenes. La concentración analítica (total) de un reactivo R en el punto i titulación viene dada por

${\displaystyle T_{{\ce {R}}}={\frac {{\ce {R}}_{0}+v_{i}{\ce {[R]}}}{v_{0}+v_{i}}}}$

donde R ₀ es la cantidad inicial de R en el recipiente de titulación, v₀ es el volumen inicial, [R] es la concentración de R en la bureta y v_i es el volumen agregado. La concentración de la bureta de un reactivo no presente en la bureta se toma como cero.

En general, la resolución de estas ecuaciones no lineales presenta un desafío formidable debido al enorme rango en el que pueden variar las concentraciones libres. Al principio, los valores para las concentraciones libres deben ser estimados. Luego, estos valores se refinan, generalmente mediante iteraciones de Newton-Raphson. Los logaritmos de las concentraciones libres pueden ser refinados en lugar de las concentraciones libres en sí mismas. El refinamiento de los logaritmos de las concentraciones libres tiene la ventaja adicional de imponer automáticamente una restricción de no negatividad en las concentraciones libres. Una vez que se han calculado las concentraciones de reactante libre, las concentraciones de los complejos se derivan de ellas y las constantes de equilibrio.

Tenga en cuenta que las concentraciones de reactantes libres pueden considerarse como parámetros implícitos en el proceso de refinamiento de la constante de equilibrio. En ese contexto, los valores de las concentraciones libres se ven limitados al obligar a que las condiciones de balance de masa se apliquen en todas las etapas del proceso.

Equilibrio constante de refinamiento

El objetivo del proceso de refinamiento es encontrar valores constantes de equilibrio que den el mejor ajuste a los datos experimentales. Esto generalmente se logra minimizando una función objetivo, U, por el método de mínimos cuadrados no lineales. Primero se definen los residuos como

${\displaystyle r_{i}=y_{i}^{\text{obs}}-y_{i}^{\text{calc}}}$

Entonces la función objetivo más general es dada por

${\displaystyle U=\sum _{i}\sum _{j}r_{i}W_{ij}r_{j}\,}$

La matriz de ponderaciones, W, debería ser, idealmente, la inversa de la matriz de varianza-covarianza de las observaciones. Es raro que esto se sepa. Sin embargo, cuando lo es, el valor esperado de U es uno, lo que significa que los datos se ajustan dentro del error experimental. La mayoría de las veces, solo se conocen los elementos diagonales, en cuyo caso la función objetivo se simplifica a

${\displaystyle U=\sum _{i}W_{ii}r_{i}^{2}}$

con W_ij = 0 cuando j ≠ i. Los pesos unitarios, W_ii = 1 , se usan a menudo, pero, en ese caso, el valor esperado de U es el cuadrado medio de la raíz de los errores experimentales.

La minimización se puede realizar utilizando el método de Gauss-Newton. En primer lugar, la función objetivo se linealiza aproximándola como una expansión de la serie de Taylor de primer orden sobre un conjunto de parámetros iniciales, p.

${\displaystyle U=U^{0}+\sum _{i}{\frac {\partial U}{\partial p_{i}}}\delta p_{i}}$

Los incrementos δp_i se agregan a los parámetros iniciales correspondientes, de modo que U es menor que U^0. Como mínimo, los derivados ∂U/∂p_i , que están simplemente relacionados con los elementos de la matriz jacobiana, J

${\displaystyle J_{jk}={\frac {\partial y_{j}^{\mathrm {calc} }}{\partial p_{k}}}}$

donde p_k es el parámetro k del refinamiento, son iguales a cero. Una o más constantes de equilibrio pueden ser parámetros del refinamiento. Sin embargo, las cantidades medidas (ver arriba) representadas por y no se expresan en términos de las constantes de equilibrio, sino en términos de las concentraciones de las especies, que son funciones implícitas de estos parámetros. Por lo tanto, los elementos jacobianos deben obtenerse mediante la diferenciación implícita.

Los incrementos de los parámetros δp se calculan resolviendo las ecuaciones normales, derivadas de las condiciones que ∂U/∂p = 0 como mínimo.

${\displaystyle \mathbf {\left(J^{\mathrm {T} }WJ\right)\delta p=J^{\mathrm {T} }Wr} }$

Los incrementos δp se agregan iterativamente a los parámetros.

${\displaystyle \mathbf {p} ^{n+1}=\mathbf {p} ^{n}+\delta \mathbf {p} }$

donde n es un número de iteración. Las concentraciones de las especies y^calc valores de y^calc se recalculan en cada punto de datos. Las iteraciones se continúan hasta que no se logre una reducción significativa en U, es decir, hasta que se satisfaga un criterio de convergencia. Sin embargo, si los parámetros actualizados no producen una disminución de la función objetivo, es decir, si se produce una divergencia, el cálculo del incremento debe modificarse. La modificación más simple es usar una fracción, f , de incremento calculado, denominado corte de desplazamiento.

${\displaystyle \mathbf {p} ^{n+1}=\mathbf {p} ^{n}+f\mathbf {\delta p} }$

En este caso, la dirección del vector de desplazamiento, δp, no se modifica. Con el algoritmo de Levenberg-Marquardt más poderoso, por otra parte, el vector de desplazamiento se gira hacia la dirección de mayor pendiente, modificando las ecuaciones normales,

${\displaystyle \mathbf {\left(J^{\mathrm {T} }WJ+\lambda I\right)\delta p=J^{\mathrm {T} }Wr} }$

donde λ es el parámetro de Marquardt e I es una matriz de identidad. Se han propuesto otros métodos para manejar la divergencia.[5]​

Un problema particular surge con la RMN y los datos espectrofotométricos. Para este último, la cantidad observada es absorbancia, A, y la ley de Beer-Lambert se puede escribir como

${\displaystyle A_{\lambda }=l\sum (\varepsilon _{pq..})_{\lambda }c_{pq..}}$

Se puede ver que, asumiendo que las concentraciones, c, son conocidas, que la absorbancia, A, a una longitud de onda dada, ${\displaystyle \lambda }$ y longitud del camino ${\displaystyle l}$, es una función lineal de las absorbptividades molares, ε. Con 1 cm de longitud de recorrido, en notación matricial.

${\displaystyle \mathbf {A} ={\boldsymbol {\varepsilon }}\mathbf {C} \,}$

Existen dos enfoques para el cálculo de las absortividades molares desconocidas.

(1) Los valores ε se consideran parámetros de la minimización y el jacobiano se construye sobre esa base. Sin embargo, los valores de ε sí mismos se calculan en cada paso del refinamiento por mínimos cuadrados lineales: ${\displaystyle {\boldsymbol {\varepsilon }}=\mathbf {\left(C^{\mathrm {T} }C\right)^{-1}C^{\mathrm {T} }A} }$

usando los valores refinados de las constantes de equilibrio para obtener la especiación. La matriz ${\displaystyle \mathbf {\left(C^{T}C\right)^{-1}C^{T}} }$

Es un ejemplo de un pseudoinverso .

Golub y Pereyra[6]​ mostraron cómo se puede diferenciar la pseudoinversa de modo que los incrementos de los parámetros tanto para la capacidad de absorción molar como para las constantes de equilibrio se puedan calcular resolviendo las ecuaciones normales.

(2) La ley de Beer-Lambert se escribe como ${\displaystyle \mathbf {\boldsymbol {\varepsilon }} _{\lambda }=\mathbf {A} _{\lambda }^{-1}\mathbf {C} \,}$

Las absorbancias molares desconocidas de todas las especies "coloreadas" se encuentran utilizando el método no iterativo de mínimos cuadrados lineales, una longitud de onda a la vez. Los cálculos se realizan una vez en cada ciclo de refinamiento, utilizando los valores constantes de estabilidad obtenidos en ese ciclo de refinamiento para calcular los valores de concentración de las especies en la matriz ${\displaystyle \mathbf {C} }$.

Errores de parámetros y correlación

En la región cercana al mínimo de la función objetivo, U, el sistema se aproxima a un sistema lineal de mínimos cuadrados, para el cual

${\displaystyle \mathbf {p=\left(J^{\mathrm {T} }WJ\right)^{-1}J^{\mathrm {T} }Wy^{\mathrm {obs} }} }$

Por lo tanto, los valores de los parámetros son (aproximadamente) combinaciones lineales de los valores de los datos observados y los errores en los parámetros, p, se pueden obtener por propagación de error de las observaciones, y^obs, usando la fórmula lineal. Deje que la matriz de varianza-covarianza para las observaciones se denote por Σ^y la de los parámetros por Σ^p. Entonces,

${\displaystyle \mathbf {\Sigma ^{p}=\left(J^{\mathrm {T} }WJ\right)^{-1}J^{\mathrm {T} }W\Sigma ^{y}W^{\mathrm {T} }J(J^{\mathrm {T} }WJ)^{-1}} }$

Cuando W = (Σ^y)^−1, esto se simplifica a

${\displaystyle \mathbf {\Sigma ^{p}=\left(J^{\mathrm {T} }WJ\right)^{-1}} }$

En la mayoría de los casos, los errores en las observaciones no están correlacionados, de modo que Σ^y es diagonal . Si es así, cada peso debe ser el recíproco de la varianza de la observación correspondiente. Por ejemplo, en una titulación potenciométrica, el peso en un punto de titulación, k, puede ser dado por

${\displaystyle W_{k}={\frac {1}{\sigma _{E}^{2}+\left({\frac {\partial E}{\partial v}}\right)_{k}^{2}\sigma _{v}^{2}}}}$

donde σ_E es el error en el potencial del electrodo o pH, (∂E/∂v)
k es la pendiente de la curva de titulación y σ_v es el error en el volumen agregado.

Cuando se utilizan pesos unitarios ( W = I , p = (J^TJ)^−1J^Ty ), se da a entender que los errores experimentales no están correlacionados y son iguales: Σ^y = σ^2I , donde σ^2 se conoce como varianza de una observación de peso unitario, y I es una matriz de identidad. En este caso σ^2 se aproxima por

${\displaystyle \sigma ^{2}={\frac {U}{n_{\mathrm {d} }-n_{\mathrm {p} }}}}$

donde U es el valor mínimo de la función objetivo y n_d y n_p son el número de datos y parámetros, respectivamente.

${\displaystyle \mathbf {\Sigma ^{p}} ={\frac {U}{n_{\mathrm {d} }-n_{\mathrm {p} }}}\left(\mathbf {J} ^{\mathrm {T} }\mathbf {J} \right)^{-1}}$

En todos los casos, la varianza del parámetro p_i viene dada por Σp
ii y la covarianza entre los parámetros p_i y p_j viene dada por Σp
ij . La desviación estándar es la raíz cuadrada de la varianza. Estas estimaciones de error reflejan solo errores aleatorios en las mediciones. La verdadera incertidumbre en los parámetros es mayor debido a la presencia de errores sistemáticos, que, por definición, no se pueden cuantificar.

Tenga en cuenta que aunque las observaciones pueden no estar correlacionadas, los parámetros siempre están correlacionados.

Constantes derivadas

Cuando las constantes acumulativas se han refinado, a menudo es útil derivar constantes por pasos a partir de ellas. El procedimiento general es anotar las expresiones de definición para todas las constantes involucradas y luego igualar las concentraciones. Por ejemplo, supongamos que se desea obtener el pKa para eliminar un protón de un ácido tribásico, LH₃, como el ácido cítrico.

${\displaystyle {\begin{aligned}{\ce {L^3-}}+{\ce {H+ <=>}}\ {\ce {LH^2-}}&:\ [{\ce {LH^2-}}]=\beta _{11}[{\ce {L^3-}}][{\ce {H+}}]\\{\ce {L^3-}}+{\ce {2H+ <=>}}\ {\ce {LH2^-}}&:\ [{\ce {LH2^-}}]=\beta _{12}[{\ce {L^3-}}][{\ce {H+}}]^{2}\\{\ce {L^3-}}+{\ce {3H+ <=>}}\ {\ce {LH3}}&:\ [{\ce {LH3}}]=\beta _{13}[{\ce {L^3-}}][{\ce {H+}}]^{3}\end{aligned}}}$

La constante de asociación paso a paso para la formación de LH₃ está dada por

${\displaystyle {\ce {{LH2^{-}}+H+<=>LH3\ ;\quad \ [LH3]}}=K[{\ce {LH2^{-}}}][{\ce {H+}}]}$

Sustituye las expresiones por las concentraciones de LH₃ y LH−
2 en esta ecuación

${\displaystyle \beta _{13}[{\ce {L^3-}}][{\ce {H+}}]^{3}=K\beta _{12}[{\ce {L^3-}}][{\ce {H+}}]^{2}[{\ce {H+}}]}$

De donde

${\displaystyle \beta _{13}=K\beta _{12};K={\frac {\beta _{13}}{\beta _{12}}}\,}$

y como pK_a = −log₁₀ 1/K su valor viene dado por

${\displaystyle {\ce {p}}K_{{\ce {a1}}}=\log _{10}\beta _{13}-\log _{10}\beta _{12}\,}$

${\displaystyle {\ce {p}}K_{{\ce {a2}}}=\log _{10}\beta _{12}-\log _{10}\beta _{11}\,}$

${\displaystyle {\ce {p}}K_{{\ce {a3}}}=\log _{10}\beta _{11}\,}$

Note la numeración inversa para pK y log β. Al calcular el error en la constante escalonada, debe tenerse en cuenta el hecho de que las constantes acumulativas están correlacionadas. Por propagación de error

${\displaystyle \sigma _{K}^{2}=\sigma _{\beta _{12}}^{2}+\sigma _{\beta _{13}}^{2}-2\sigma _{\beta _{12}}\sigma _{\beta _{13}}\rho _{12,13}\,}$

y

${\displaystyle \sigma _{\log _{10}K}={\frac {\sigma _{K}}{K}}}$

Selección de modelo

Una vez que se haya completado un refinamiento, se deben verificar los resultados para verificar que el modelo elegido sea aceptable. En términos generales, un modelo es aceptable cuando los datos se ajustan a un error experimental, pero no hay un criterio único para usar para hacer el juicio. Lo siguiente debe ser considerado.

La función objetiva

Cuando los pesos se han derivado correctamente de las estimaciones de error experimental, el valor de expectativa de U/n_d − n_p es 1.[7]​ Por lo tanto, es muy útil estimar errores experimentales y derivar algunos pesos razonables de ellos, ya que es un indicador absoluto de la bondad del ajuste.

Cuando se usan los pesos unitarios, se implica que todas las observaciones tienen la misma varianza. Se espera que U/n_d − n_p sea igual a esa varianza.

Errores de parámetros

Uno querría que los errores en las constantes de estabilidad sean aproximadamente proporcionales al error experimental. Por ejemplo, con los datos de titulación del pH, si el pH se mide con 2 decimales, los errores de log₁₀ β no deben ser mucho mayores que 0.01. En trabajos exploratorios donde la naturaleza de las especies presentes no se conoce de antemano, se pueden probar y comparar varios modelos químicos diferentes. Habrá modelos donde las incertidumbres en la mejor estimación de una constante de equilibrio pueden ser algo o incluso significativamente mayores que el σ_pH, especialmente con aquellas constantes que gobiernan la formación de especies comparativamente menores, pero la decisión de cuán grande es aceptable sigue siendo subjetiva. El proceso de decisión sobre si incluir o no equilibrios comparativamente inciertos en un modelo, y para la comparación de modelos competitivos en general, puede ser objetivo y ha sido descrito por Hamilton.[7]​

Distribución de residuos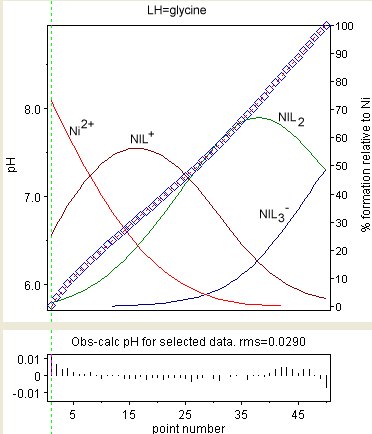

Como mínimo en U el sistema puede aproximarse a uno lineal, los residuos en el caso de pesos unitarios están relacionados con las observaciones por

${\displaystyle \mathbf {r=y^{\mathrm {obs} }-J\left(J^{\mathrm {T} }T\right)^{-1}J^{\mathrm {T} }y^{\mathrm {obs} }} }$

El simétrica, idempotente matriz J(J^TT)^−1J es conocido en la literatura estadística como la matriz de sombrero , H Así,

${\displaystyle \mathbf {r=\left(I-H\right)y^{\mathrm {obs} }} }$

y

${\displaystyle \mathbf {M^{r}=\left(I-H\right)M^{y}\left(I-H\right)} }$

donde I es una matriz de identidad y M^r y M^y son las matrices de varianza-covarianza de los residuos y observaciones, respectivamente. Esto muestra que aunque las observaciones pueden no estar correlacionadas, los residuos siempre están correlacionados.

El diagrama de la derecha muestra el resultado de un refinamiento de las constantes de estabilidad de Ni (Gly)^+, Ni (Gly)₂ y Ni(Gly)−
3 (donde Gly = glicina). Los valores observados se muestran como diamantes azules y las concentraciones de las especies, como porcentaje del níquel total, se superponen. Los residuos se muestran en el cuadro inferior. Los residuos no se distribuyen tan aleatoriamente como se esperaría. Esto se debe a la variación de los potenciales de unión líquida y otros efectos en las interfaces de vidrio/líquido. Esos efectos son muy lentos en comparación con la velocidad a la que se establece el equilibrio.

Restricciones físicas

Algunas restricciones físicas son usualmente incorporadas en los cálculos. Por ejemplo, todas las concentraciones de reactantes libres y especies deben tener valores positivos y las constantes de asociación deben tener valores positivos.

Con los datos espectrofotométricos, todos los valores de absortividad (o emisividad) molar deberían ser positivos. La mayoría de los programas de computadora no imponen esta restricción en los cálculos.

Otros modelos

Si el modelo no es aceptable, se debe examinar una variedad de otros modelos para encontrar el que mejor se ajuste a los datos experimentales, dentro del error experimental. La principal dificultad es con las llamadas especies menores. Estas son especies cuya concentración es tan baja que el efecto en la cantidad medida está en o por debajo del nivel de error en la medición experimental. La constante para una especie menor puede resultar imposible de determinar si no hay medios para aumentar la concentración de la especie. .

Implementaciones

Algunos sistemas simples son susceptibles de cálculos de hoja de cálculo.[8]​ Se ha publicado un gran número de programas de computadora para el cálculo de la constante de equilibrio.[9]​ Los programas más utilizados son:

• Datos potenciométricos: Hyperquad , BEST[10]​ PSEQUAD[11]​
• Datos espectrofotométricos: HypSpec, SQUAD,[11]​ Specfit,[12]​ ReactLab EQUILIBRIA .
• RMN de datos de RMNMR, EQNMR Archivado el 14 de julio de 2019 en Wayback Machine.
• Datos calorimétricos HypΔH. Afinímetro

Los calorímetros de titulación isotérmicos comerciales generalmente se suministran con un software con el que se puede obtener una constante de equilibrio y una entalpía de formación estándar para la formación de un aducto 1:1. También se puede suministrar algún software para manejar equilibrios más complejos.

Referencias

1. Rossotti, F. J. C.; Rossotti, H. (1961). The Determination of Stability Constants. McGraw-Hill. 
2. «Definitions of pH scales, standard reference values, measurement of pH, and related terminology». Pure Appl. Chem. 57: 531-542. 1985. doi:10.1351/pac198557030531. 
3. Silva, Andre M. N.; Kong, Xiaole; Hider, Robert C. (2009). «Determination of the pK_a value of the hydroxyl group in the α-hydroxycarboxylates citrate, malate and lactate by ^13C NMR: implications for metal coordination in biological systems». Biometals 22 (5): 771-778. PMID 19288211. doi:10.1007/s10534-009-9224-5. 
4. Motekaitis, R. J.; Martell, A. E. (1982). «BEST — A new program for rigorous calculation of equilibrium parameters of complex multicomponent systems». Can. J. Chem. 60: 2403-2409. doi:10.1139/v82-347. 
5. Potvin, P. G. (1990). «Modelling complex solution equilibria. I. Fast, worry-free least-squares refinement of equilibrium constants». Can. J. Chem. 68: 2198-2207. doi:10.1139/v90-337. 
6. Golub, G. H.; Pereyra, V. (1973). «The Differentiation of Pseudo-Inverses and Nonlinear Least Squares Problems Whose Variables Separate». SIAM J. Numer. Anal. 2: 413-432. Bibcode:1973SJNA...10..413G. doi:10.1137/0710036. 
7. Hamilton, W. C. (1964). Statistics in Physical Science. New York, NY: Ronald Press. 
8. Billo, E. Joseph (2011). Excel for Chemists: A Comprehensive Guide (3rd edición). Wiley-VCH. ISBN 978-0-470-38123-6. 
9. Gans, P.; Sabatini, A.; Vacca, A. (1996). Talanta 43. pp. 1739-1753. PMID 18966661. doi:10.1016/0039-9140(96)01958-3. 
10. Martell, A. E.; Motekaitis, R. J. (1992). The Determination and Use of Stability Constants. Wiley-VCH. ISBN 0471188174. 
11. Leggett, D. J., ed. (1985). Computational Methods for the Determination of Formation Constants. Plenum Press. ISBN 978-0-306-41957-7. 
12. Gampp, H.; Maeder, M.; Mayer, C. J.; Zuberbühler, A. (1985). «Calculation of equilibrium constants from multiwavelength spectroscopic data—IMathematical considerations». Talanta 32 (95): 257. PMID 18963802. doi:10.1016/0039-9140(85)80035-7. 

• Datos: Q3045347