Cálculo del esqueleto

Ejemplos de esqueletos de formas simples.
Una forma y su esqueleto

Para calcular los esqueletos existe una clase de algoritmos utilizados en el análisis de las formas. Se trata de reducir una forma en un conjunto de curvas, llamadas esqueletos, centradas en la forma original. El cálculo del esqueleto es una herramienta de análisis no-escalar de formas, que conserva las propiedades topológicas de la forma original así como las propiedades geométricas, según el método utilizado.

Definiciones y propiedades

En términos simples, el cálculo del esqueleto consiste en adelgazar una forma hasta obtener un conjunto de curvas centradas. El conjunto resultante es entonces denominado esqueleto o eje medio.

En la literatura técnica, los conceptos esqueleto y eje medio son utilizados indistintamente por algunos autores,[1]​[2]​[3]​[4]​[5]​ mientras que otros autores[6]​[7]​[8]​ los consideran relacionados, pero que no son idénticos. Del mismo modo, los conceptos cálculo del esqueleto y adelgazamiento también son considerados como iguales por parte de algunos,[2]​ y no por otros.[6]​

Existen diferentes definiciones para el cálculo del esqueleto.

La analogía del fuego en la pradera

La siguiente definición fue enunciada por Harry Blum y se conoce como la analogía del fuego en la pradera. Ofrece una visión intuitiva del cálculo del esqueleto.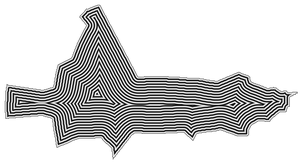

Evolución del frente de fuego en una forma.

Sea una pradera cubierta homogéneamente por la hierba seca y Ω un conjunto de puntos en esta pradera. Inicialmente, todos los puntos del contorno de Ω se encienden simultáneamente. El fuego se propaga de manera uniforme y se extiende a través de la pradera a una velocidad constante. El esqueleto del conjunto de puntos Ω (denotado MA(Ω)) se define como el lugar geométrico de los puntos donde los frentes de fuego se reúnen.

Definición formal

Existe una definición formal del esqueleto basada en el concepto de discos o bolas máximos (maximales). El esqueleto de una forma S, denotada MA(S), se define por el conjunto de los centros de los discos (bolas) máximos (maximales) en S.

Esqueleto ponderado

El esqueleto ponderado o la transformación del eje medio de una forma S, denotada MAT(S), es el conjunto de pares compuestos del centro y radio de los discos (bolas) máximos de S.

Exoesqueleto y endoesqueleto

Los esqueletos no son solo los objetos ubicados dentro de las formas. Si retomamos la analogía del fuego en la pradera, el proceso de cálculo del esqueleto no sólo transforma el interior de la forma, sino también el exterior. Luego, se denomina endoesqueleto a la parte del esqueleto que se encuentra dentro de la forma y exoesqueleto a la parte del esqueleto que se encuentra fuera de la forma.

A menudo la confusión se da entre esqueleto y endoesqueleto, ya que esta parte del esqueleto es la más estudiada en el análisis de las formas. Del mismo modo, en este artículo, consideramos que los esqueletos corresponden a endoesqueletos.

Propiedades de los esqueletos

Los esqueletos tienen varias propiedades interesantes:

  • los esqueletos son teóricamente invariantes bajo las transformaciones lineales (traslación, rotación y cambio de escala),
  • el cálculo de un esqueleto es una transformación homotópica: conserva las propiedades topológicas de la forma.

Otras propiedades son específicas de los esqueletos ponderados:

  • todos los esqueletos ponderados son únicos,
  • en el caso de los esqueletos ponderados, el cálculo del esqueleto es una transformación reversible en el sentido de que es posible reconstruir la forma original a partir del esqueleto ponderado,
  • un esqueleto ponderado proporciona una descripción jerárquica de la forma: los puntos del esqueleto alejados del contorno describen la apariencia general de la forma y los puntos del esqueleto más cercanos al contorno describen las particularidades que aparecen en este.

Otra propiedad de los esqueletos se considera, en general, un defecto: el cálculo del esqueleto es una transformación semi-continua. En efecto, la más mínima alteración en el contorno o en el interior de la forma puede producir la creación de una rama importante en el esqueleto.

Métodos para calcular los esqueletos

Existe una gran variedad de métodos para construir los esqueletos a partir de las formas. En la mayoría de las publicaciones científicas, los métodos de cálculo de los esqueletos se pueden clasificar en cuatro clases.

Adelgazamiento topológico

El adelgazamiento topológico consiste en retirar “en su justa medida” los puntos del contorno de la forma, preservando sus características topológicas. Los puntos del esqueleto son añadidos cuando se forma una esquina (la curva del contorno se hace discontinua) o cuando los puntos del contorno se reúnen.

La extracción del mapa de distancias

El mapa de distancias de una forma S consiste en asociar a cada punto de S su distancia al punto más cercano del contorno.

Una de las definiciones del esqueleto mediante la función de la distancia es como las 'crestas' (aquellos puntos en que la función distancia disminuye a ambos lados) de la función de la distancia.[6]​ Existe un malentendido en la literatura de que el esqueleto consiste de los puntos que son "máximos locales" en la transformación de distancia. Esto no es cierto como aun una rápida comparación de una transformación de distancia y el esqueleto resultante puede mostrar.

Simulación del frente de fuego

Los métodos que trabajan mediante la simulación del frente de fuego se basan en la analogía del fuego en la pradera. Ellos estudian la evolución del frente de fuego a través del tiempo. Cada formación de choque en el frente se agrega al esqueleto.

Cálculo analítico

La búsqueda del esqueleto está relacionado con un problema geométrico. Los métodos de esta clase utilizan herramientas geométricas, tales como el diagrama de Voronoï o la poligonización de las curvas de nivel (en el caso del cálculo del esqueleto en los espacios discretos).

Otros criterios de clasificación

Los métodos de cálculo del esqueleto se pueden clasificar según el tipo de espacio al que se aplican. Algunos métodos de cálculo del esqueleto se aplican a espacios continuos. Estos métodos son generalmente exactos y precisos. Otros métodos de cálculo del esqueleto se aplican a espacios discretos. Estos métodos son precisos solo en algunos casos y requieren frecuentemente de una secuencia de operaciones para afinar el esqueleto.

Algunos métodos de cálculo del esqueleto se aplican a formas en un plano o a objetos tridimensionales y más.

Aplicaciones

El cálculo de esqueletos tiene muchas aplicaciones, tales como el reconocimiento de patrones, el modelado de sólidos para el diseño y la manipulación de formas, la organización de la dispersión (nubes de puntos), la búsqueda de caminos, animaciones, etc. Se utiliza en la medicina y la biología desde sus inicios, así como en mineralogía. Se han encontrado aplicaciones en la indexación de imágenes en las bases de datos y en compresión. No hay más que unas pocas aplicaciones en la arquitectura y el urbanismo, en el contexto del análisis morfológico.

Los investigadores han demostrado que, en el proceso de la percepción visual, nuestra sensibilidad inconsciente es máxima en el esqueleto.

Orígenes

El cálculo de esqueletos es un método que fue desarrollado originalmente en los años sesenta por Harry Blum, para crear un nuevo descriptor de formas. Este método ha ganado el interés de muchos investigadores. En la actualidad, el cálculo de esqueletos es un método bien conocido en el análisis de imágenes. Hay muchos algoritmos propuestos para transformar una forma en esqueleto.

Referencias

  1. ↑ Jain, Ramesh; Kasturi, Rangachar; Schunck, Brian G. (1995), Machine Vision, ISBN 0-07-032018-7 ., Section 2.5.10, p. 55.
  2. ↑ a b Gonzales, Rafael C.; Woods, Richard E. (2001), Digital Image Processing, ISBN 0-201-18075-8 ., Section 11.1.5, p. 650
  3. ↑ http://people.csail.mit.edu/polina/papers/skeletons_cvpr00.pdf
  4. ↑ Dougherty, Edward R. (1992), An Introduction to Morphological Image Processing, ISBN 0-8194-0845-X .
  5. ↑ Ogniewicz, R. L. (1995), «Automatic Medial Axis Pruning Based on Characteristics of the Skeleton-Space», en Dori, D.; Bruckstein, A., eds., Shape, Structure and Pattern Recognition, ISBN 981-02-2239-4 .
  6. ↑ a b c Jain, Anil K. (1989), Fundamentals of Digital Image Processing, ISBN 0-13-336165-9 .., Section 9.9, p. 382.
  7. ↑ Serra, Jean (1982), Image Analysis and Mathematical Morphology, ISBN 0126372403 .
  8. ↑ Sethian, J. A. (1999), Level Set Methods and Fast Marching Methods, ISBN 0-521-64557-3 ., Section 17.5.2, p. 234.

Bibliografía

  • Dominique Attali. Squelettes et graphes de Voronoï 2D et 3D. Thèse de doctorat, Université Joseph Fourier - Grenoble I, octobre 1995.
  • Harry Blum. A transformation for extracting new descriptors of shape. In Wathen Dunn, editor, Proceedings of Models for the Perception of Speech and Visual Form, pages 362-380. MIT Press, 1967.
  • Frédéric Fol-Leymarie. Three-dimensional shape representation via schock flows. PhD thesis, Brown University, Providence, Rhode Island, USA, May 2003. 209 p.
  • Benjamin B. Kimia. On the role of medial geometry in human vision. Journal of Physiology, 97(2–3):155–190, March-May 2003.
  • Sven Loncaric. A survey of shape analysis techniques. Pattern Recognition, 31(8):983-1001, 1998.