En los esfuerzos de mejora de procesos, el índice de capacidad del proceso, Cpk, también denominado ratio de capacidad del proceso, es un cálculo estadístico sobre la capacidad del proceso: la capacidad de un proceso para producir un resultado dentro de límites predefinidos (TS, tolerancia superior; TI, tolerancia inferior). El concepto de capacidad del proceso es solo válido para procesos que están en estado de control estadístico. Los índices de capacidad del proceso miden cuánta "variación natural" experimenta un proceso en relación con sus límites de especificación y permite comparar qué tan bien controla una organización diferentes procesos.[cita requerida]
Este índice juega un papel fundamental en las plantas de producción al tratar de demostrar que un proceso (por ejemplo, de producción de tornillos) es fiable y está bajo control.[cita requerida]
Límites de especificación
Si los límites superior e inferior de la especificación (en inglés "Upper Specification Limit", USL; y "Lower Specification Limit" o LSL) de un proceso son TS y TI, la media objetivo del proceso es T (del inglés "Target"), la media estimada del proceso es  y la variabilidad estimada del proceso (expresada como desviación estándar) es
y la variabilidad estimada del proceso (expresada como desviación estándar) es  , entonces algunos índices comunes de capacidad del proceso aceptados son:
, entonces algunos índices comunes de capacidad del proceso aceptados son:
| Índice
|
Descripción
|

|
Calcula lo que el proceso sería capaz de producir si el proceso estuviera centrado. Presupone que el resultado del proceso sigue una distribución normal.
|

|
Calcula la capacidad del proceso para especificaciones únicamente con un límite inferior (ej. fuerza). Presupone que el resultado del proceso está aproximadamente distribuido de forma normal.
|

|
Calcula la capacidad del proceso para especificaciones únicamente con un límite superior (ej. concentración). Presupone que el resultado del proceso esta aproximadamente distribuido de forma normal.
|
![{\displaystyle {\hat {C}}_{pk}=\min {\Bigg [}{{\text{TS}}-{\hat {\mu }} \over 3\times {\hat {\sigma }}},{{\hat {\mu }}-{\text{TI}} \over 3\times {\hat {\sigma }}}{\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3274fde4e6ef9aac02851a56456d044d7173b74)
|
Calcula lo que el proceso es capaz de producir si el objetivo del proceso está centrado entre los límites de la especificación. En caso de que la media del proceso no este centrada,  sobreestima la capacidad del proceso. sobreestima la capacidad del proceso.  si la media del proceso se sitúa fuera de los límites de especificación. Presupone que el resultado del proceso esta aproximadamente distribuido de forma normal. si la media del proceso se sitúa fuera de los límites de especificación. Presupone que el resultado del proceso esta aproximadamente distribuido de forma normal.
|

|
Calcula la capacidad del proceso respecto a un objetivo, T.  es siempre mayor que cero. Presupone que el resultado del proceso esta aproximadamente distribuido de forma normal. es siempre mayor que cero. Presupone que el resultado del proceso esta aproximadamente distribuido de forma normal.
|

|
Calcula la capacidad del proceso respecto a un objetivo, T válido para un proceso con una media descentrada. Presupone que el resultado del proceso esta aproximadamente distribuido de forma normal.
|
 se estima usando la desviación estándar de muestreo.
se estima usando la desviación estándar de muestreo.
Valores recomendados
Los índices de capacidad de proceso enfatizan la necesidad de mejorar la capacidad del proceso cuando mayores son. Valores próximos o por debajo de uno indican que el proceso no está centrado ( lejos de T) o bien son inestables.
lejos de T) o bien son inestables.
Un valor del índice de capacidad del proceso aceptable no es algo de carácter general. Las metas de una empresa así como el sector o centro de producción afectado incluso el proceso en observación, pueden contar con diferentes objetivos diferentes para el índice. Por ejemplo, en la industria automotriz, el Grupo de Acción de la Industria Automotriz (AIAG por sus siglas en inglés) estipula cuatro guías en el Proceso de Aprobación de Partes de Producción (PPAP), la cuarta edición recomienda unos valores mínimos de Cpk para que se alcancen características de proceso críticas para la calidad. Sin embargo, estos criterios son cuestionables y no se puede evaluar la capacidad de varios procesos porque no han sido definidos adecuadamente.
Puesto que la capacidad del proceso es una función de la especificación, el índice de capacidad del proceso únicamente es tan bueno como la especificación. Por ejemplo, si la especificación viene de una guía de ingeniería sin consideración de la función y la criticidad de la parte, no tiene utilidad una discusión sobre la capacidad del proceso, y sería más beneficioso si se enfocaran los esfuerzos en definir cuáles son los riesgos reales de tener una parte que se sale de los límites de especificación. La función de pérdida de los métodos de Taguchi ilustra mejor este concepto.
Al menos un experto académico recomienda[1] lo siguiente:
| Caso
|
Recomendación de capacidad mínima de proceso para especificaciones con 2 límites
|
Recomendación de capacidad mínima de proceso para especificaciones con 1 límite
|
| Proceso existente
|
1,33
|
1,25
|
| Proceso nuevo
|
1,50
|
1,45
|
| Parámetros críticos o de seguridad para procesos existentes
|
1,50
|
1,45
|
| Parámetros críticos o de seguridad para procesos nuevos
|
1,67
|
1,60
|
| Proceso de calidad de Six Sigma
|
2,00
|
2,00
|
Es importante destacar que en casos en los que el índice Cpk de un proceso es superior a 2.5, disminuir este índice puede resultar caro sin un beneficio directo.[2]
Ejemplo
Considere una característica de calidad con un objetivo de 100.00 μm y límites de especificación superior e inferior de 106.00 μm y 94 μm respectivamente. Si después de supervisar el proceso cuidadosamente por un rato, parece que el proceso está bajo control y produce salidas con previsibilidad (como se muestra en el gráfico de ejecución de abajo), podemos estimar significativamente su media y desviación estándar.
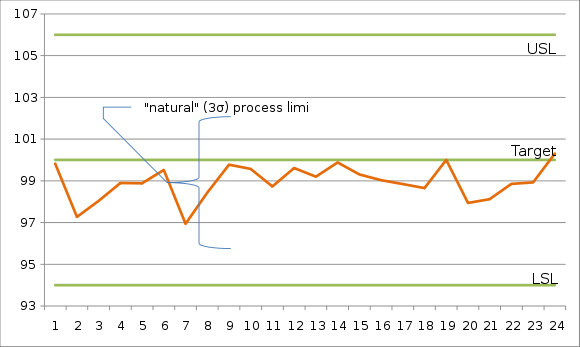
Si  y
y  se estiman ser 98.94 μm y 1.03 μm, respectivamente, entonces:
se estiman ser 98.94 μm y 1.03 μm, respectivamente, entonces:
| Índice
|

|
![{\displaystyle {\hat {C}}_{pk}=\min {\Bigg [}{{\text{TS}}-{\hat {\mu }} \over 3{\hat {\sigma }}},{{\hat {\mu }}-{\text{TI}} \over 3{\hat {\sigma }}}{\Bigg ]}=\min {\Bigg [}{106.00-98.94 \over 3\times 1.03},{98.94-94 \over 3\times 1.03}{\Bigg ]}=1.60}](https://wikimedia.org/api/rest_v1/media/math/render/svg/303bae6c0d8768bdef354bb39957404a393fae8a)
|

|

|
El hecho de que el proceso se ejecute fuera del centro (cerca de 1σ debajo de su objetivo) está reflejado en los valores marcadamente diferentes para Cp, Cpk, Cp. m., y Cpkm.
Referencias
- ↑ Douglas Montgomery (2004). Introduction to Statistical Quality Control. Nueva York: John Wiley & Sons, Inc. p. 776. ISBN 9780471656319.
- ↑ Booker, J. M.; Raines, M.; Swift, K. G. (2001). Designing capable and reliable products. Oxford [England]: Butterworth Heinemann. ISBN 0-7506-5076-1.
Véase también
Enlaces externos





![{\displaystyle {\hat {C}}_{pk}=\min {\Bigg [}{{\text{TS}}-{\hat {\mu }} \over 3\times {\hat {\sigma }}},{{\hat {\mu }}-{\text{TI}} \over 3\times {\hat {\sigma }}}{\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3274fde4e6ef9aac02851a56456d044d7173b74)







![{\displaystyle {\hat {C}}_{pk}=\min {\Bigg [}{{\text{TS}}-{\hat {\mu }} \over 3{\hat {\sigma }}},{{\hat {\mu }}-{\text{TI}} \over 3{\hat {\sigma }}}{\Bigg ]}=\min {\Bigg [}{106.00-98.94 \over 3\times 1.03},{98.94-94 \over 3\times 1.03}{\Bigg ]}=1.60}](https://wikimedia.org/api/rest_v1/media/math/render/svg/303bae6c0d8768bdef354bb39957404a393fae8a)

